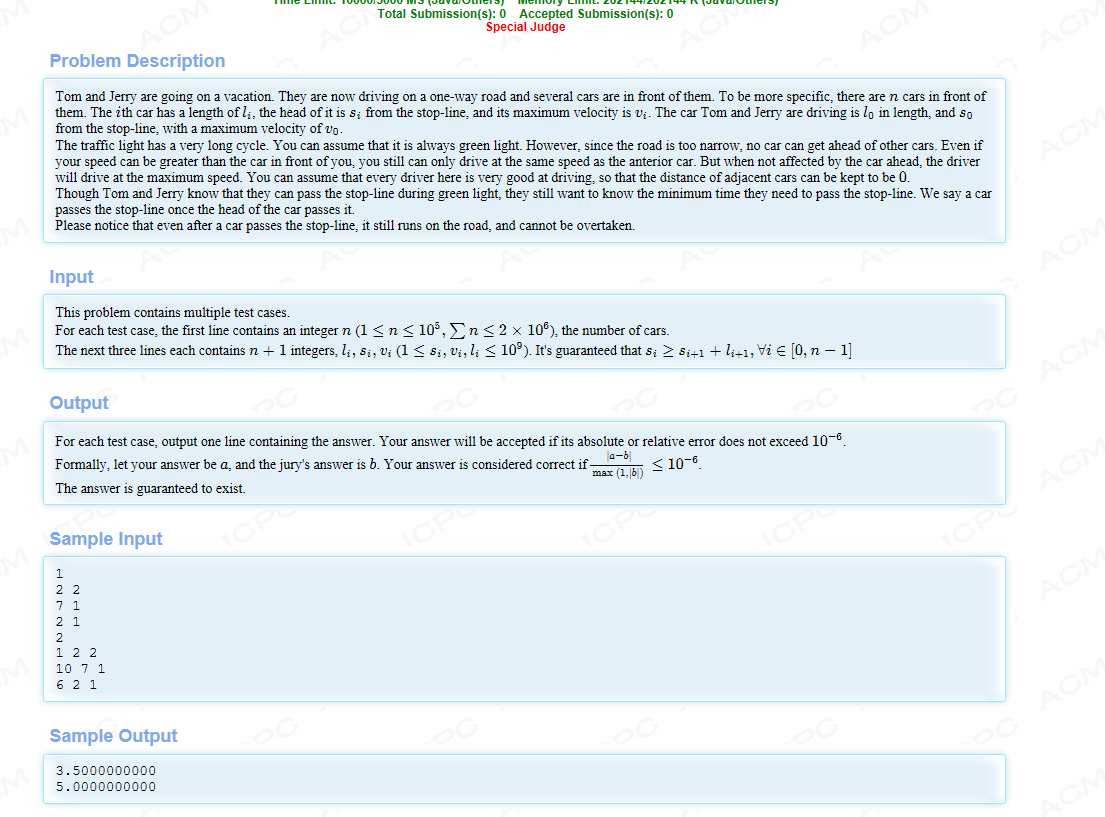
题目看上去倒是蛮复杂的样子嘞!

Vacation的更多相关文章

  1. 【BZOJ】【3550】【ONTAK2010】Vacation

    网络流/费用流 Orz太神犇了这题…… 我一开始想成跟Intervals那题一样了……每个数a[i]相当于覆盖了(a[i]-n,a[i]+n)这个区间……但是这样是错的!!随便就找出反例了……我居然还 ...

  2. BZOJ3550: [ONTAK2010]Vacation

    3550: [ONTAK2010]Vacation Time Limit: 10 Sec  Memory Limit: 96 MBSubmit: 91  Solved: 71[Submit][Stat ...

  3. uva 10192 Vacation（最长公共子）

    uva 10192 Vacation The Problem You are planning to take some rest and to go out on vacation, but you ...

  4. 568. Maximum Vacation Days

    Problem statement:  LeetCode wants to give one of its best employees the option to travel among N ci ...

  5. [LeetCode] Maximum Vacation Days 最大化休假日

    LeetCode wants to give one of its best employees the option to travel among N cities to collect algo ...

  6. Atcoder C - Vacation （ DP ）

    C - Vacation Time Limit: 2 sec / Memory Limit: 1024 MB Score : 100100 points Problem Statement Taro' ...

  7. Holiday、Vacation、Days off、Leave、Break

    http://write.scu.edu.tw/view.php?bd=mistake&no=25 這些字在英文的用法中都有放假.休息的意思,但用法卻不太一樣,接下來就來看看它們的不同吧. 『 ...

  8. bzoj 4097: [Usaco2013 dec]Vacation Planning

    4097: [Usaco2013 dec]Vacation Planning Description Air Bovinia is planning to connect the N farms (1 ...

  9. UVA.10192 Vacation (DP LCS)

    UVA.10192 Vacation (DP LCS) 题意分析 某人要指定旅游路线,父母分别给出了一系列城市的旅游顺序,求满足父母建议的最大的城市数量是多少. 对于父母的建议分别作为2个子串,对其做 ...

  10. BZOJ_3550_[ONTAK2010]Vacation&&BZOJ_1283:_序列_网络流解线性规划

    BZOJ_3550_[ONTAK2010]Vacation&&BZOJ_1283:_序列_网络流解线性规划 Description 给出一个长度为 的正整数序列Ci,求一个子序列,使得 ...

随机推荐

  1. 解读Ubuntu的sources.list 和soucres.litsd

    使用过Ubuntu的道友们都知道,默认地址是乌班图的org 配置的,对于国内长途跋涉的各位高手来讲真是艰辛: 所以我们一般在安装的时候会先修改服务器源地址使用国内的比如ali,清华或者华为的 源文件地 ...

  2. 使用ScrollRect制作翻页

    1.标准的层级结构 ScrollRect->ViewPort->Content,Viewport负责显示区域的大小一般和Mask一起配合使用,Content使用Layout来布局,如果想使 ...

  3. 控制台测试ajax

    有的时候需要测试下web项目中post.get请求是否正确,但是这个时候电脑上没有安装测试工具,怎么办呢?直接用浏览器控制台测试,打开网站,F12控制台,在控制台下复制粘贴下面的ajax请求,之后aj ...

  4. pandas处理csv，分组统计

    需求: /tmp/demo/data下有10个csv文件,按col0和col1分组分别统计col2和col3总和并计算col2和col3的商 # encoding:utf-8 import panda ...

  5. spring security和java web token整合

    思路: spring security 1.用户输入用户名密码. 2.验证:从库中(可以是内存.数据库等)查询该用户的密码.角色,验证用户名和密码是否正确.如果正确,则将填充Authenticatio ...

  6. Codeforces Round #622 (Div. 2)C（单调栈，DP)

    构造出的结果一定是一个单峰/\这种样子的 #define HAVE_STRUCT_TIMESPEC #include<bits/stdc++.h> using namespace std; ...

  7. Gin_入门

    1. 创建路由 1.1 Restful风格的API gin支持Restful风格的API 即Representational State Transfer的缩写.直接翻译的意思是"表现层状态 ...

  8. 【JS】网站运行时间

    <span id="sitetime"></span> <script language=javascript> function siteTi ...

  9. my bug of VG algorithm

    def visibility_graph(series): g = nx.Graph() # convert list of magnitudes into list of tuples that h ...

  10. MySql5.6表操作

    MySql5.6表操作 数据类型 整型 浮点型 字符类型 日期类型 枚举类型与集合类型 约束条件 Primary key Unique key Not null Foreign key 创建表的完整语 ...