@bzoj - 4356@ Ceoi2014 Wall

目录

• @description@
• @solution@
• @accepted code@
• @details@

---

@description@

给出一个N*M的网格图，有一些方格里面存在城市，其中首都位于网格图的左上角。

你可以沿着网络的边界走，要求你走的路线是一个环并且所有城市都要被你走出来的环圈起来，即想从方格图的外面走到任意一个城市一定要和你走的路线相交。

你沿着方格的边界走是需要费用的，不同的边界费用可能不同，求最小代价。

1<=N,M<=400,走过边界的代价为正整数且不超过10^9

Sample Input

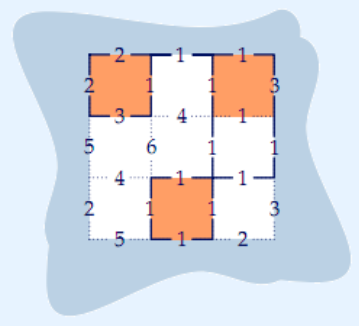
3 3

1 0 1

0 0 0

0 1 0

2 1 1 3

5 6 1 1

2 1 1 3

2 1 1

3 4 1

4 1 1

5 1 2

Sample Output

22

HINT

@solution@

人类智慧题。

首先路径可能重复经过边或者点这件事很难描述，而且本身很不自然。

我们将走过一条边看成两种，一种从左/上侧经过，一种从右/下侧经过（竖着的边就是左右侧，横着的边就是上下侧）。

比如下图就是转变后的例子：

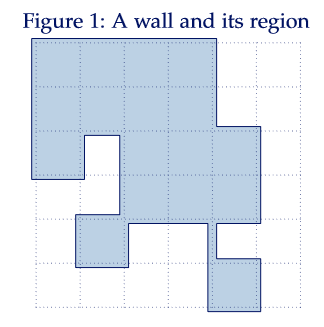
这样就不会经过重边重点，而且可以很自然地描述包含一条边/一个格点的概念。

假如没有额外限制，就只是找一个简单最小环（并且一定包含左上角，因为左上角一定有一个城市）。

如果左上角的格点为 (0, 0)，那么跑一个从 (0, 1) 到 (1, 0) 的最短路即可。

但是我怎么表达包含一个城市的概念。

假如只有左上角有城市，则只要确定起点为 (0, 1) 终点为 (1, 0) 就可以包含左上角的城市了。

假如城市与城市之间有些割不断的联系，那么我跑最短路时不横断这些联系，既然我已经包含了左上角，就可以保证所有城市都在最小环里面了。

有一个结论：左上角的格点到城市的左上角的最短路一定会被包含其中。

直观地理解：

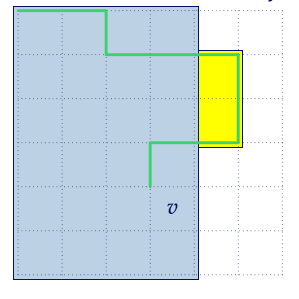
假如蓝色是一种方案，绿色是最短路。当我把黄色区域加入进去过后，因为是最短路，所以方案一定不会变差（否则绿色就不是最短路了）。

即我们总可以用最短路代替边界。

那么建出最短路树，只要不横断这些树边就一定合法了。

具体实现，我们将一个格点拆成四个，建出一个类似于如下的图：

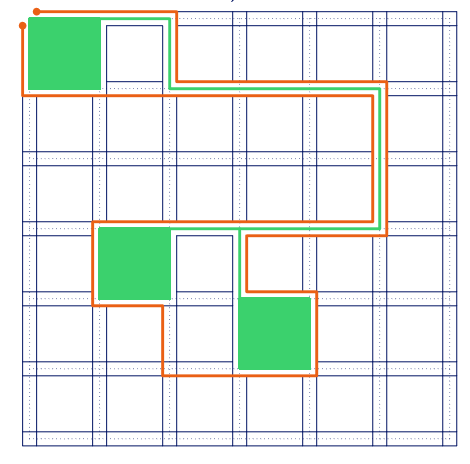
拆出来的四个点之间，如果不会横断最短路就连边权为 0 的边。

同时需要注意，一个城市四个角对应的点不向其他点连边。

左上角的格点拆出来的对应左上角的那个点不连边，跑左上角的格点对应的右上角到左上角的格点对应左下角的那个点的最短路。

两个相邻格点之间也要连，边权即原图中边的边权。

@accepted code@

#include<cstdio>
#include<queue>
#include<algorithm>
using namespace std;
#define rep(G, x) for(Graph::edge *p = G.adj[x];p;p = p->nxt)
typedef long long ll;
const int MAXN = 400 + 5;
const int MAXV = 4*MAXN*MAXN;
const int MAXE = 16*MAXV + 5;
const ll INF = (1LL<<60);
struct Graph{
	struct edge{
		int to, dis;
		edge *nxt;
	}edges[MAXE + 5], *adj[MAXV + 5], *ecnt;
	Graph() {ecnt = edges;}
	void addedge(int u, int v, int w) {
		edge *p = (++ecnt);
		p->to = v, p->dis = w, p->nxt = adj[u], adj[u] = p;
		p = (++ecnt);
		p->to = u, p->dis = w, p->nxt = adj[v], adj[v] = p;
//		printf("! %d %d %d\n", u, v, w);
	}
	void clear(int n) {
		ecnt = edges;
		for(int i=1;i<=n;i++)
			adj[i] = NULL;
	}
}G;
int hp[MAXV + 5], pre[MAXV + 5];
ll f[MAXV + 5], dis[MAXV + 5];
void update(int x, ll k, const int &n) {
	f[x] = k;
	while( x ) {
		hp[x] = x;
		if( (x<<1) <= n && f[hp[x<<1]] < f[hp[x]] )
			hp[x] = hp[x<<1];
		if( (x<<1|1) <= n && f[hp[x<<1|1]] < f[hp[x]] )
			hp[x] = hp[x<<1|1];
		x >>= 1;
	}
}
void dijkstra(int s, const int &n) {
	for(int i=1;i<=n;i++)
		dis[i] = f[i] = INF, hp[i] = i;
	update(s, dis[s] = 0, n);
	while( f[hp[1]] != INF ) {
		int x = hp[1]; update(x, INF, n);
		rep(G, x) {
			if( dis[x] + p->dis < dis[p->to] ) {
				update(p->to, dis[p->to] = dis[x] + p->dis, n);
				pre[p->to] = x;
			}
		}
	}
}
int id[MAXN + 5][MAXN + 5], cnt;
int A[MAXN + 5][MAXN + 5], B[MAXN + 5][MAXN + 5], C[MAXN + 5][MAXN + 5];
bool tg[MAXV + 5];
queue<int>que;
int ind(int x, int p) {
	return (x - 1) * 4 + p;
}
bool check(int x, int y) {
	return (pre[x] == y && tg[x]) || (pre[y] == x && tg[y]);
}
int main() {
	int N, M; scanf("%d%d", &N, &M);
	for(int i=1;i<=N;i++)
		for(int j=1;j<=M;j++)
			scanf("%d", &A[i][j]);
	for(int i=1;i<=N+1;i++)
		for(int j=1;j<=M+1;j++)
			id[i][j] = (++cnt);
	for(int i=1;i<=N;i++)
		for(int j=1;j<=M+1;j++) {
			scanf("%d", &B[i][j]);
			G.addedge(id[i][j], id[i+1][j], B[i][j]);
		}
	for(int i=1;i<=N+1;i++)
		for(int j=1;j<=M;j++) {
			scanf("%d", &C[i][j]);
			G.addedge(id[i][j], id[i][j+1], C[i][j]);
		}
	dijkstra(1, cnt);
	for(int i=1;i<=N;i++)
		for(int j=1;j<=M;j++)
			if( A[i][j] ) que.push(id[i][j]), tg[id[i][j]] = true;
	while( !que.empty() ) {
		int f = que.front(); que.pop();
		if( !tg[pre[f]] )
			que.push(pre[f]), tg[pre[f]] = true;
	}
	G.clear(cnt);
	for(int i=1;i<=N;i++)
		for(int j=1;j<=M+1;j++) {
			if( !A[i][j-1] )
				G.addedge(ind(id[i][j], 3), ind(id[i+1][j], 2), B[i][j]);
			if( !A[i][j] )
				G.addedge(ind(id[i][j], 4), ind(id[i+1][j], 1), B[i][j]);
		}
	for(int i=1;i<=N+1;i++)
		for(int j=1;j<=M;j++) {
			if( !A[i-1][j] )
				G.addedge(ind(id[i][j], 1), ind(id[i][j+1], 2), C[i][j]);
			if( !A[i][j] )
				G.addedge(ind(id[i][j], 4), ind(id[i][j+1], 3), C[i][j]);
		}
	for(int i=1;i<=N+1;i++)
		for(int j=1;j<=M+1;j++) {
			if( i == 1 && j == 1 ) continue;
			if( !(check(id[i][j], id[i-1][j]) || A[i-1][j] || A[i-1][j-1]) )
				G.addedge(ind(id[i][j], 1), ind(id[i][j], 2), 0);
			if( !(check(id[i][j], id[i][j-1]) || A[i][j-1] || A[i-1][j-1]) )
				G.addedge(ind(id[i][j], 2), ind(id[i][j], 3), 0);
			if( !(check(id[i][j], id[i+1][j]) || A[i][j-1] || A[i][j]) )
				G.addedge(ind(id[i][j], 3), ind(id[i][j], 4), 0);
			if( !(check(id[i][j], id[i][j+1]) || A[i-1][j] || A[i][j]) )
				G.addedge(ind(id[i][j], 4), ind(id[i][j], 1), 0);
		}
	dijkstra(ind(1, 1), ind(cnt, 4));
	printf("%lld\n", dis[ind(1, 3)]);
}

@details@

只用了 N 没有用 M 这个变量的人一定不止我一个人吧。

所以 2014 年出的题我现在还是不会。