数据结构之 AVL个人笔记

从这位前辈的博客园中学习的数据结构：https://www.cnblogs.com/skywang12345/

非常感谢这位前辈。

以下文章摘录于 :skywang12345的博客园：转载请注明出处：http://www.cnblogs.com/skywang12345/p/3576969.html

及自我的一些理解。

首先介绍下AVL树：

　　AVL树：二叉树的一种，其名为：平衡二叉查找树、高度平衡树。其表现形式为：AVL树中的任何节点的两个子树，它们的高度相差最大为1。即HEIGHT <= 1；

　　如下图：

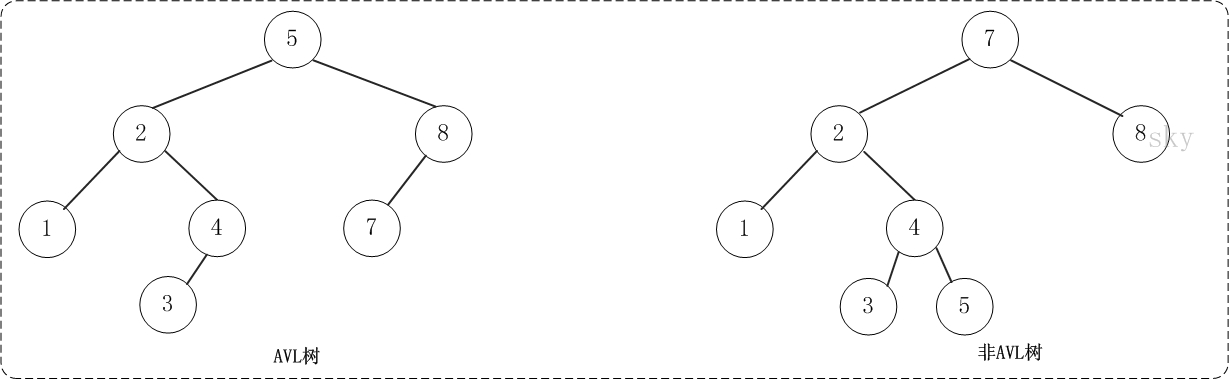
　　AVL树的查找、插入和删除在平均和最坏情况下都是O(logn)。

　　如果在AVL树中插入或删除节点后，使得高度之差大于1。此时，AVL树的平衡状态就被破坏，它就不再是一棵二叉树；为了让它重新维持在一个平衡状态，就需要对其进行旋转处理。学AVL树，重点的地方也就是它的旋转算法；

　　AVL树失去平衡的几种情况：

　　（1）

　　

　　（2）

　　

　　这种失去平衡的可以概括为4种姿态：LL(左左)，LR(左右)，RR(右右)和RL(右左)。

　　　　LL: 失去平衡的节点为：左节点的左孩子，即左节点的左孩子也有了左（右）孩子

　　　　LR: 失去平衡的节点为：左节点的右孩子，即左节点的右孩子也有了左（右）孩子

　　　　RR: 失去平衡的节点为：右节点的右孩子，即右节点的右孩子也有了左（右）孩子

　　　　RL: 失去平衡的节点为：右节点的左孩子，即右节点的左孩子也有了左（右）孩子

　　0.定义

　　

typedef struct AVLTreeNode{
    Type key;  //关键值
    struct AVLTreeNode *left;  //左孩子
    struct AVLTreeNode *right; //右孩子
    int height; //高度
}Node,*AVLTree;

//使用条件表达式时，最外面的大括号不能丢，如果丢了的话会造成数据的计算错误
#define AVL_HEIGHT(p)    ( (p == NULL)?0:( ((AVLTree)(p))->height ) )
#define MAX(a,b)   ( ((a) > (b) )? (a) : (b)  ） 

　　1.创建AVLTree的节点

　　

AVLTree creatAVLTreeNode(Type key, AVLTree left, AVLTree right) //高度并不是人为决定的
{
    AVLTree p;
    if ((p = (AVLTree)malloc(sizeof(Node))) == NULL)
    {
        printf("malloc ERROR in %s\n",__FUNCTIONW__);
        return ;
    }
    p->height = ;
    p->key = key;
    p->left = left;
    p->right = right;
}

　　2.获取AVLTree的高度

//获取AVLTree的高度
//树的高度为最大层次。即空的二叉树的高度是0，非空树的高度等于它的最大层次(根的层次为1，根的子节点为第2层，依次类推)。
int GetAVLTreeHeight(AVLTree tree)
{
    return AVL_HEIGHT(tree);
}

　　3.对于各种情况的旋转处理

/*
* LL：左左对应的情况(左单旋转)。 称为：右旋
*
* 返回值：旋转后的根节点
*/
static AVLTree left_left_rotation(AVLTree k2)
{
    AVLTree k1;

    k1 = k2->left;
    k2->left = k1->right;
    k1->right = k2;

    k2->height = MAX((GetAVLTreeHeight(k2->left)), (GetAVLTreeHeight(k2->right))) +; //加上本身节点高度，根节点高度为1
    k1->height = MAX((GetAVLTreeHeight(k1->left)),k2->height) + ; //加上本身节点高度，根节点高度为1

    return k1;
}

/*
* RR：右右对应的情况(右单旋转)。称为：左旋
*
* 返回值：旋转后的根节点
*/
static AVLTree right_right_rotation(AVLTree k1)
{
    AVLTree k2;

    k2 = k1->right;
    k1->right = k2->left;
    k2->left = k1;

    k1->height = MAX( AVL_HEIGHT(k1->left), AVL_HEIGHT(k1->right) ) + ;
    k2->height = MAX(k1->height, AVL_HEIGHT(k2->right)) + ;
    return k2;
}

/*
* LR：左右对应的情况(先右旋转，再左旋转)。
*
* 返回值：旋转后的根节点
*/
static AVLTree left_right_rotation(AVLTree k3)
{
    //1. 进行 RR单旋转
    k3->left = right_right_rotation(k3);
    //2. 进行 LL单旋转
    return left_left_rotation(k3);
}

/*
* RL：右左对应的情况(先左旋转，再右旋转)。
*
* 返回值：旋转后的根节点
*/
static AVLTree right_left_rotation(AVLTree k3)
{
    //1. 进行 LL单旋转
    k3->left = left_left_rotation(k3);
    //2. 进行 RR单旋转
    return right_right_rotation(k3);
}

　　4.插入

/*
* 3. 插入
* 将结点插入到AVL树中，并返回根节点
*
* 参数说明：
*     tree AVL树的根结点
*     key 插入的结点的键值
* 返回值：
*     根节点
*/
AVLTree avltree_insert(AVLTree tree, Type key)
{

    if (tree == NULL) //如果树为空的，则将key作为根节点
    {
        if ((tree = creatAVLTreeNode(key, NULL, NULL)) == NULL)
        {
            printf("creatNode ERROR in %s \n",__FUNCTIONW__);
            return NULL;
        }
    }
    else if (key < tree->key) //根据二叉树特性，将key插入左节点
    {
        tree->left = avltree_insert(tree->left, key);

        //插入节点后，进行平衡树的检查
        if (AVL_HEIGHT(tree->left) - AVL_HEIGHT(tree->right) ==  ) //因为插入的是左节点，所以是left-right;
        {
            if (key < tree->left->key) //判断是LR 还是LL；
                tree = left_left_rotation(tree);
            else
                tree = left_right_rotation(tree);
        }
    }
    else if (key > tree->key)
    {
        tree->right = avltree_insert(tree->right, key);
        //插入节点后，进行平衡树的检查
        if (AVL_HEIGHT(tree->right) - AVL_HEIGHT(tree->left) == )
        {
            if (key > tree->left->key) //判断是RR 还是RL；
                tree = right_right_rotation(tree);
            else
                tree = right_left_rotation(tree);
        }
    }
    else //(key == tree->key)
        printf("添加失败：不允许添加相同的节点！\n");

    tree->height = MAX(AVL_HEIGHT(tree->left),AVL_HEIGHT(tree->right)) + ;
    return tree;

}

　　5.查找key值

//4.查找key值
AVLTree AVLTree_search(AVLTree tree, Type key)
{
    if (tree == NULL || key == tree->key)
        return tree;
    if (key > tree->key)
        return AVLTree_search(tree->right, key);
    else
        return AVLTree_search(tree->left, key);
}

//5.查找最大值 与 最小值的节点
AVLTree AVLTreeMaxNode(AVLTree tree)
{
    if (tree == NULL)
        return NULL;
    while (tree->right != NULL)
        tree = tree->right;
    return tree;
}
AVLTree AVLTreeMinNode(AVLTree tree)
{
    if (tree == NULL)
        return NULL;
    while (tree->left != NULL)
        tree = tree->left;
    return tree;
}

　　6.删除节点

/*
* 6.删除结点(z)，返回根节点
*
* 参数说明：
*     ptree AVL树的根结点
*     z 待删除的结点
* 返回值：
*     根节点
*/
static AVLTree delete_node(AVLTree tree, AVLTree z)
{
    // 根为空 或者 没有要删除的节点，直接返回NULL。
    if (tree == NULL || z == NULL)
        return NULL;

    if (z->key < tree->key)        // 待删除的节点在"tree的左子树"中
    {
        tree->left = delete_node(tree->left,z);

        // 删除节点后，若AVL树失去平衡，则进行相应的调节。
        if (AVL_HEIGHT(tree->right) - AVL_HEIGHT(tree->left) == )
        {
            Node *r = tree->right;

            //判断是哪种失去平衡情况：
            //如果删除的节点在左子树中，则说明删除后就看根节点的右孩子里的情况就好，相当于第一个为Rx（先右旋，再x旋）
            //如果左孩子的高度大于右孩子的根则是 RL，反之亦然，下同
            if (AVL_HEIGHT(r->left) > AVL_HEIGHT(r->right))
                tree = right_left_rotation(tree);
            else
                tree = right_right_rotation(tree);
        }
    }
    else if (z->key > tree->key)// 待删除的节点在"tree的右子树"中
    {
        tree->right = delete_node(tree->right, z);
        // 删除节点后，若AVL树失去平衡，则进行相应的调节。
        if (AVL_HEIGHT(tree->left) - AVL_HEIGHT(tree->right) == )
        {
            Node *l = tree->left;
            if (AVL_HEIGHT(l->right) > AVL_HEIGHT(l->left))
                tree = left_right_rotation(tree);
            else
                tree = left_left_rotation(tree);
        }
    }
    else // tree是对应要删除的节点。
    {
        if (tree->left && tree->right) //如果待删除的节点左右孩子都不为空
        {
            if (HEIGHT(tree->left) > HEIGHT(tree->right))
            {
                // 如果tree的左子树比右子树高；
                // 则(01)找出tree的左子树中的最大节点
                //   (02)将该最大节点的值赋值给tree。
                //   (03)删除该最大节点。
                // 这类似于用"tree的左子树中最大节点"做"tree"的替身；
                // 采用这种方式的好处是：删除"tree的左子树中最大节点"之后，AVL树仍然是平衡的。
                Node *max = AVLTreeMaxNode(tree->left);
                tree->key = max->key;
                tree->left = delete_node(tree->left, max);
            }
            else
            {
                // 如果tree的左子树不比右子树高(即它们相等，或右子树比左子树高1)
                // 则(01)找出tree的右子树中的最小节点
                //   (02)将该最小节点的值赋值给tree。
                //   (03)删除该最小节点。
                // 这类似于用"tree的右子树中最小节点"做"tree"的替身；
                // 采用这种方式的好处是：删除"tree的右子树中最小节点"之后，AVL树仍然是平衡的。
                Node *min = AVLTreeMinNode(tree->right);
                tree->key = min->key;
                tree->right = delete_node(tree->right, min);
            }
        }
    }
}