noip模拟29

这次终于是早上考试了

早上考试手感不错，这次刷新了以前的最高排名～

%%%cyh巨佬 \(rk1\)

%%%CT巨佬 \(t2\) 90

纵观前几，似乎我 \(t3\) 是最低的……

总计挂分10分，\(t2\) 写的 \(exgcd\) 因为变量打错没用上

---

A. 最长不下降子序列

第一眼看上去没思路……

看见 \(n\) 的范围太大了，估计得从数列生成上做文章

一开始研究了半天二次函数之类的东西，试图寻找单调性之类的东东

后来索性不会还是打个表找规律吧

咦？居然循环了？

（这个样例给的刁钻呀）其实换个什么别的模数或者初始项很快就会出现循环节

冷静分析一下，因为模数很小，前一项经过函数作用后结果是固定的，那么最多出现模数个数后就会出现循环

那循环就简单了，有几个循环就有几个相等数，循环节内部也会有，把第一个拿出来和前面的跑个LIS拼一下完事儿

然后写个对拍，发现Wa了！！！

开始手模，发现有一种很神奇的情况，比如：

14523 14523 14523

乍一看前面是3加上后面两个是5，但其实是6

冷静分析一下发现这种情况只有把前 \(len\) 个循环节都揪出去跑才能解决

赶紧改一下然后就过了

代码实现

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=1e6+5;
int n,t[maxn],a,b,c,d,last[maxn],ed,num,len,st,st1,ans,f[maxn],cc[maxn];
void add(int x,int w){
	x++;
	for(;x<=151;x+=x&-x){
		cc[x]=max(cc[x],w);
	}
	return ;
}
int ask(int x){
	x++;
	int ans=0;
	for(;x;x-=x&-x)ans=max(ans,cc[x]);
	return ans;
}
signed main(){
//	freopen("lis0.in","r",stdin);
//	freopen("my.out","w",stdout);
	cin>>n;
	cin>>t[1]>>a>>b>>c>>d;
	if(n<=100000){
		for(int i=2;i<=n;i++){
			t[i]=(a*t[i-1]*t[i-1]+b*t[i-1]+c)%d;
		}
		for(int i=1;i<=n;i++){
			f[i]=1;
			f[i]=max(f[i],ask(t[i])+1);
			add(t[i],f[i]);
			ans=max(ans,f[i]);
		}
		cout<<ans;
		return 0;
	}
	last[t[1]]=1;
	for(int i=2;i<=n;i++){
		t[i]=(a*t[i-1]*t[i-1]+b*t[i-1]+c)%d;
		if(last[t[i]]){
			st=last[t[i]];
			len=i-last[t[i]];
			break;
		}
		last[t[i]]=i;
	}
	for(int i=st+len;i<=st+len*(len+10);i++){
		t[i]=(a*t[i-1]*t[i-1]+b*t[i-1]+c)%d;
	}
	num=(n-st+1)/len-len;
	ed=n-num*len;
	for(int i=1;i<=ed;i++){
		f[i]=1;
		f[i]=max(f[i],ask(t[i])+1);
		add(t[i],f[i]);
	}
	st1=ed+1;
	for(int i=st1;i<=st1+len-1;i++){
		for(int j=1;j<=ed;j++){
			if(t[j]<=t[i])ans=max(ans,f[j]);
		}
	}
	cout<<ans+num;
	return 0;
}

---

考完看题解，还有一种不同的方法

对于循环节的 LIS 采用 \(dp\) 的方式

设 \(f[n][i][j]\) 表示以第一个循环节 \(i\) 开头，以后面第 \(n\) 个循环节的 \(j\) 结尾的 LIS 长度，转移：

\[f[n][i][j]=\max_{1\le k \le T,a[i]\le a[k]\le a[j]}(f[n-1][i][k]+f[1][k][j])
\]

然后用了一个很神奇的方法优化一下——广义矩阵乘法

正常的矩乘是先乘后加，发现形式和这个很像，这不过这个是先加后 \(max\)，只要把矩乘定义该一下就好了

把 \(F[1]\) 看成 \(base\) 矩阵，那么 \(F[n]=F[n-1]*base\)，这样可以矩阵快速幂了

然后 \(F[1]\) 暴力算一下即可

---

B. 完全背包问题

考场上想过同余最短路，但是看见还有总和不超过 \(C\) 的限制条件就直接跑路了，然后转数学，开始裴蜀定理乱搞，搞不出来

正解就是同余最短路，但是得加个分层来满足限制条件

先来根据同余最短路的套路来设个方程：

\(f[j][k]\) 表示选了的物品模 \(val[0]\) 等于 \(j\)，且选了 \(k\) 个物品的最小总价值（之所以是最小，因为最后要加许多个 \(val[0]\)，最小的可以表示出全部状态）

转移：

\[f[j][k]+val[i]->f[(j+val[i])\%val[0]][k] (val[i]<L)
\]

\[f[j][k]+val[i]->f[(j+val[i])\%val[0]][k+1] (val[i]\ge L)
\]

发现如果点开成一维的不好转移，那么再加一维代表层数，转移即可

代码实现

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fi first
#define se second
const int maxn=55,maxm=10005;
int n,m,limit,sum,val[maxn],w,dis[maxm][maxn];
bool vis[maxm][maxn];
int read(){
	int x=0,f=1;
	char ch=getchar();
	while(!isdigit(ch)){
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(isdigit(ch)){
		x=x*10+ch-48;
		ch=getchar();
	}
	return x*f;
}
struct Node{
	pair<int,int>id;
	int dis;
	Node(){}
	Node(pair<int,int>x,int y):id(x),dis(y){}
	bool operator < (const Node & x)const{
		return dis>x.dis;
	}
};
priority_queue<Node>q;
void dij(){
	memset(dis,0x3f,sizeof dis);
	dis[0][0]=0;
	q.push(Node(make_pair(0,0),0));
	while(!q.empty()){
		pair<int,int>x=q.top().id;
		q.pop();
		if(vis[x.fi][x.se])continue;
		vis[x.fi][x.se]=true;
		for(int i=2;i<=n;i++){
			if(val[i]>=limit&&x.se==sum)break;
			if(val[i]<limit){
				if(dis[(x.fi+val[i])%val[1]][x.se]>dis[x.fi][x.se]+val[i]){
					dis[(x.fi+val[i])%val[1]][x.se]=dis[x.fi][x.se]+val[i];
					q.push(Node(make_pair((x.fi+val[i])%val[1],x.se),dis[(x.fi+val[i])%val[1]][x.se]));
				}
			}
			else{
				if(dis[(x.fi+val[i])%val[1]][x.se+1]>dis[x.fi][x.se]+val[i]){
					dis[(x.fi+val[i])%val[1]][x.se+1]=dis[x.fi][x.se]+val[i];
					q.push(Node(make_pair((x.fi+val[i])%val[1],x.se+1),dis[(x.fi+val[i])%val[1]][x.se+1]));
				}
			}
		}
	}
	return ;
}
signed main(){
	n=read();
	m=read();
	for(int i=1;i<=n;i++)val[i]=read();
	sort(val+1,val+n+1);
	limit=read();
	sum=read();
	dij();
	for(int i=1;i<=m;i++){
		w=read();
		bool flag=false;
		for(int j=0;j<=sum;j++){
			if(w>=dis[w%val[1]][j]){
				flag=true;
				break;
			}
		}
		if(flag)puts("Yes");
		else puts("No");
	}
	return 0;
}

---

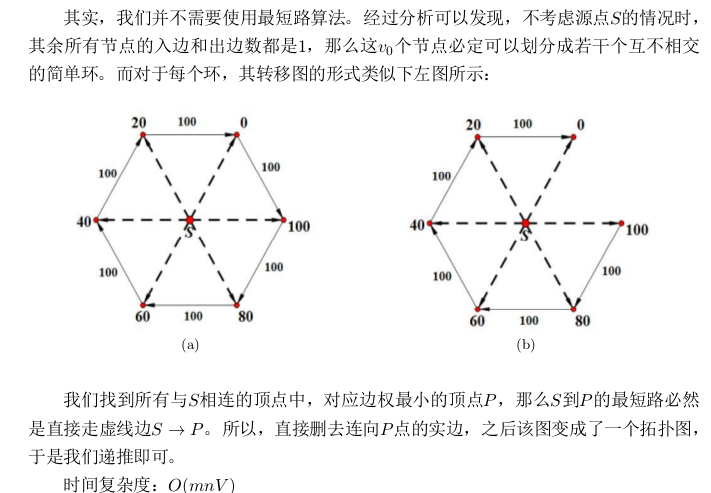
题解上介绍了复杂度更优的方法：

---

C. 最近公共祖先

每次修改一个点的时候，暴力跳 \(father\)，这是祖先的权值对其他子树是有贡献的，在 \(dfs\) 上修改即可

由于每个节点只有第一次走到父亲是有用的，所以最多更新 \(n\) 次，复杂度正确