【剑指offer】8：跳台阶

题目描述：

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

解题思路：

这种题目多为找规律求通用公式并最终用代码实现。

首先，考虑最简单的情况就是1个台阶，即仅有1种跳法；2个台阶，有2种跳法；3个台阶，有3种跳法；4个台阶，有5种跳法；5个台阶，有8种跳法……

即1,2,3,5,8,13……

我们从以上规律不难发现该题本质上就是斐波拉契数列，只是稍作改动

公式总结为：

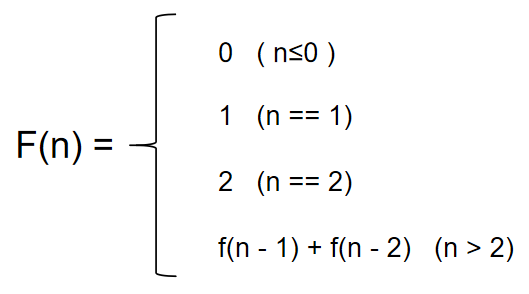
由以上公式不难看出，本题可以直接采用和第七题一样的思路进行解答即可。

代码实现

（C实现）：

int jumpFloor(int number ) {
    // write code here
    int fir = 1, sec = 2,res;
    if (number <= 0 || number == 1 || number == 2) return number;
    //  return jumpFloor(number - 1) + jumpFloor(number - 2);     递归方式
    for (int i = 2; i < number; i++)
    {
        res = fir + sec;
        fir = sec;
        sec = res;
    }
}

（JavaScript实现）：

function jumpFloor(number)
{
    // write code here
    if (number <= 0 || number == 1 || number == 2) {
　　　　return number;
　　}    
    //  return jumpFloor(number - 1) + jumpFloor(number - 2);   递归方法
    var fir = 1, sec = 2, res;
    for (var i = 2; i < number; i++) {
        res = fir + sec;
        fir = sec;
        sec = res;
    }
    return res;
}