Delaunay 三角化 学习3

简介

还是太菜从解析官方代码开始。

官方代码共有三个核心函数。

参考链接

http://blog.sina.com.cn/s/blog_6029f0330101irlh.html

http://paulbourke.net/papers/triangulate/triangulate.c 官方代码 ？

https://www.geeksforgeeks.org/equation-of-circle-when-three-points-on-the-circle-are-given/ 求圆心坐标的代码

首先关于二维的知道三点如何求解圆心

设定方程为 \(A(x^2 + y^2) + Dx + Ey + F = 0\)

如果知道不在一条直线上的三点\((x_1,y_1),(x_2,y_2),(x_3,y_3)\),那么我们可以使用克拉默法则来求解联立方程组

\[\left\{\begin{array}{l}
A\left(x^{2}+y^{2}\right)+D x+E y+F=0 \\
A\left(x_{1}^{2}+y_{1}^{2}\right)+D x_{1}+E y_{1}+F=0 \\
A\left(x_{2}^{2}+y_{2}^{2}\right)+D x_{2}+E y_{2}+F=0 \\
A\left(x_{3}^{2}+y_{3}^{2}\right)+D x_{3}+E y_{3}+F=0
\end{array}\right.
\]

则个构成关于A,D,E,F的四元线性方程组，有非零解的充要条件是系数行列式的值为0

\[\left|\begin{array}{llll}
x^{2}+y^{2} & x & y & 1 \\
x_{1}^{2}+y_{1}^{2} & x_{1} & y_{1} & 1 \\
x_{2}^{2}+y_{2}^{2} & x_{2} & y_{2} & 1 \\
x_{3}^{2}+y_{3}^{2} & x_{3} & y_{3} & 1
\end{array}\right|=0
\]

（至于为什么，有人知道可以发在评论区里面，我忘了）。

师弟的解答：如果不为0的话那么ADEF都为0一定是其中的解，那么就没有意义了。

当任意点(x,y)与已知三点的某一点重合和，则有两行完全相同行列式为0，表明已知三点满足这个方程。如果这样感觉应该有无穷多个解，四个未知量，只有三个方程组。

若将系数行列式按照第一行展开可得

\[\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\left(x^{2}+y^{2}\right)-\left|\begin{array}{lll}
x_{1}^{2}+y_{1}^{2} & y_{1} & 1 \\
x_{2}^{2}+y_{2}^{2} & y_{2} & 1 \\
x_{3}^{2}+y_{3}^{2} & y_{3} & 1
\end{array}\right| x+\left|\begin{array}{lll}
x_{1}^{2}+y_{1}^{2} & x_{1} & 1 \\
x_{2}^{2}+y_{2}^{2} & x_{2} & 1 \\
x_{3}^{2}+y_{3}^{2} & x_{3} & 1
\end{array}\right| y-\left|\begin{array}{lll}
x_{1}^{2}+y_{1}^{2} & x_{1} & y_{1} \\
x_{2}^{2}+y_{2}^{2} & x_{2} & y_{2} \\
x_{3}^{2}+y_{3}^{2} & x_{3} & y_{3}
\end{array}\right|=0
\]

四个系数行列式依次对应着A，-D，E，-F的值。最特别的是三个方程求解出了四个未知量？其实不是的ADEF是呈现一个内在的比例的

\[\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right| \neq 0
\]

对应着三点不共线。

QU

1. 太神奇了为啥三个函数可以解除四个未知量。
   
   最特别的是三个方程求解出了四个未知量？其实不是的ADEF是呈现一个内在的比例的关系。

那如何求解圆心坐标和半径呢？

第一个看的明白点，参考链接 https://www.geeksforgeeks.org/equation-of-circle-when-three-points-on-the-circle-are-given/

code

hh

/*
 * @Author: your name
 * @Date: 2020-12-08 15:18:17
 * @LastEditTime: 2020-12-10 13:20:21
 * @LastEditors: Please set LastEditors
 * @Description: In User Settings Edit
 * @FilePath: \delaunay\cpp\cpp\Delaunay.h
 */
#ifndef Delaunay_H
#define Delaunay_H
#include <stdint.h>
#include <iostream>
#include <stdlib.h> // for C qsort
#include <cmath>
#include <time.h> // for random
#include <fstream>
#include <vector>
#include <algorithm>
const int MaxVertices = 500;
const int MaxTriangles = 1000;
const double EPSILON = 0.000001;

struct ITRIANGLE
{
  int p1, p2, p3;
};

struct IEDGE
{
  int p1, p2;
};

struct XYZ
{
  double x, y, z;
};

//int XYZCompare(const void *v1, const void *v2);
int Triangulate(int nv, XYZ pxyz[], ITRIANGLE v[], int &ntri);
bool CircumCircle(double, double, double, double, double, double, double,
                 double, double &, double &, double &);
bool genPoints(std::vector<XYZ> &points, int numPoints);
void findCircle(double x1, double y1, double x2, double y2, double x3, double y3, double &xc, double &yc, double &r);
#endif

cc

#include "Delaunay.hh"

using namespace std;

// Function to find the circle on
// which the given three points lie
void findCircle(double x1, double y1, double x2, double y2, double x3, double y3, double &xc, double &yc, double &r)
{
    double x12 = x1 - x2;
    double x13 = x1 - x3; 

    double y12 = y1 - y2;
    double y13 = y1 - y3; 

    double y31 = y3 - y1;
    double y21 = y2 - y1; 

    double x31 = x3 - x1;
    double x21 = x2 - x1; 

    // x1^2 - x3^2
    double sx13 = pow(x1, 2) - pow(x3, 2); 

    // y1^2 - y3^2
    double sy13 = pow(y1, 2) - pow(y3, 2); 

    double sx21 = pow(x2, 2) - pow(x1, 2);
    double sy21 = pow(y2, 2) - pow(y1, 2); 

    double f = ((sx13) * (x12)
             + (sy13) * (x12)
             + (sx21) * (x13)
             + (sy21) * (x13))
            / (2 * ((y31) * (x12) - (y21) * (x13)));
    double g = ((sx13) * (y12)
             + (sy13) * (y12)
             + (sx21) * (y13)
             + (sy21) * (y13))
            / (2 * ((x31) * (y12) - (x21) * (y13))); 

    double c = -pow(x1, 2) - pow(y1, 2) - 2 * g * x1 - 2 * f * y1; 

    // eqn of circle be x^2 + y^2 + 2*g*x + 2*f*y + c = 0
    // where centre is (h = -g, k = -f) and radius r
    // as r^2 = h^2 + k^2 - c
    double h = -g;
    double k = -f;
    double sqr_of_r = h * h + k * k - c; 

    // r is the radius
    r = sqrt(sqr_of_r); 

    cout << "Centre = (" << h << ", " << k << ")" << endl;
    xc = h;
    yc = k;
    cout << "Radius = " << r << endl;
} 

////////////////////////////////////////////////////////////////////////
// CircumCircle() :
//   Return true if a point (xp,yp) is inside the circumcircle made up
//   of the points (x1,y1), (x2,y2), (x3,y3)
//   The circumcircle centre is returned in (xc,yc) and the radius r
//   Note : A point on the edge is inside the circumcircle
////////////////////////////////////////////////////////////////////////
bool CircumCircle(double xp, double yp, double x1, double y1, double x2,
                 double y2, double x3, double y3, double &xc, double &yc, double &r)
{
  double m1, m2, mx1, mx2, my1, my2;
  double dx, dy, rsqr, drsqr;

  /* Check for coincident points 防止三点共线 */
  if (abs(y1 - y2) < EPSILON && abs(y2 - y3) < EPSILON){
    return false;
  }
  // if (abs(x1 - x2) < EPSILON && abs(x2 - x3) < EPSILON){
  //   return false;
  // }
  findCircle(x1, y1, x2, y2, x3, y3, xc, yc, r);
  dx = x2 - xc;
  dy = y2 - yc;
  rsqr = dx * dx + dy * dy;
  dx = xp - xc;
  dy = yp - yc;
  drsqr = dx * dx + dy * dy;
  return ((drsqr <= rsqr) ? true : false);
}
///////////////////////////////////////////////////////////////////////////////
// Triangulate() :
//   Triangulation subroutine
//   Takes as input NV vertices in array pxyz
//   Returned is a list of ntri triangular faces in the array v
//   These triangles are arranged in a consistent clockwise order.
//   The triangle array 'v' should be malloced to 3 * nv
//   The vertex array pxyz must be big enough to hold 3 more points
//   The vertex array must be sorted in increasing x values say
//
//   qsort(p,nv,sizeof(XYZ),XYZCompare);
///////////////////////////////////////////////////////////////////////////////
/**
 * @description: v存储点的序列，每三个构成一个三角形
 * @param {*}
 * @return {*}
 */
int Triangulate(std::vector<XYZ> &pxyz, std::vector<ITRIANGLE> &v)
{
  std::vector<int> complete;
  std::vector<IEDGE> edges;
  double xmin, ymin, xmax, ymax;
  /*
      Find the maximum and minimum vertex bounds.
      This is to allow calculation of the bounding triangle
  */
  int nv = pxyz.size();
  xmin = pxyz[0].x;
  ymin = pxyz[0].y;
  xmax = xmin;
  ymax = ymin;
  for (int i = 1; i < pxyz.size(); i++)
  {
    if (pxyz[i].x < xmin)
      xmin = pxyz[i].x;
    if (pxyz[i].x > xmax)
      xmax = pxyz[i].x;
    if (pxyz[i].y < ymin)
      ymin = pxyz[i].y;
    if (pxyz[i].y > ymax)
      ymax = pxyz[i].y;
  }
  double dx, dy, dmax, xmid, ymid;
  dx = xmax - xmin;
  dy = ymax - ymin;
  dmax = (dx > dy) ? dx : dy;
  xmid = (xmax + xmin) / 2.0;
  ymid = (ymax + ymin) / 2.0;
  /*
   构建一个超级三角形包含所有的点.
   超级三角形的点位于所有点的末尾。
   超级三角形式三角形列表的第一个单位
  */
  XYZ tmp;
  tmp.x = xmid - 20 * dmax;;
  tmp.y = ymid - dmax;
  pxyz.push_back(tmp);
  tmp.x = xmid;
  tmp.y = ymid + 20 * dmax;;
  pxyz.push_back(tmp);
  tmp.x = xmid + 20 * dmax;
  tmp.y = ymid - dmax;;
  pxyz.push_back(tmp);
  ITRIANGLE itmp;

  itmp.p3 = pxyz.size() - 1;
  itmp.p2 = pxyz.size() - 2;
  itmp.p1 = pxyz.size() - 3;
  v.push_back(itmp);
  complete.push_back(false);
  /*
   加入现有顶点
  */
  double xp = 0;
  double yp = 0;
  int ntri = 1;
  for (int i = 0; i < nv; i++)
  {
    xp = pxyz[i].x;
    yp = pxyz[i].y;
    /*
     设定边，如果顶点在圆的内部然后三角形的三个边加入边的buffer然后删除三角形
    */
    double x1, y1, x2, y2, x3, y3, xc, yc, r;
    bool inside = false;
    edges.clear();
    for (int j = 0; j < v.size(); j++)
    {
      if (complete[j])
        continue;
      x1 = pxyz[v[j].p1].x;
      y1 = pxyz[v[j].p1].y;
      x2 = pxyz[v[j].p2].x;
      y2 = pxyz[v[j].p2].y;
      x3 = pxyz[v[j].p3].x;
      y3 = pxyz[v[j].p3].y;
      inside = CircumCircle(xp, yp, x1, y1, x2, y2, x3, y3, xc, yc, r);
      if (xc + r < xp)
        // Suggested
        // if (xc + r + EPSILON < xp)
        complete[j] = true; //
      if (inside)
      {
        IEDGE etmp;
        etmp.p1 = v[j].p1;
        etmp.p2 = v[j].p2;
        edges.push_back(etmp);
        etmp.p1 = v[j].p2;
        etmp.p2 = v[j].p3;
        edges.push_back(etmp);
        etmp.p1 = v[j].p3;
        etmp.p2 = v[j].p1;
        edges.push_back(etmp);
        v[j] = v[v.size() - 1];
        v.pop_back();// 弹出最后一个算是删除了
        complete[j] = complete[complete.size() - 1];
        complete.pop_back();
        j--;
      }
    }
    /*
  删除所有的包围中心边。得到一个周围边
  Note: if all triangles are specified anticlockwise then all
  interior edges are opposite pointing in direction.
    */
    for (int j = 0; j < edges.size() - 1; j++)
    {
      for (int k = j + 1; k < edges.size(); k++)
      {
        if ((edges[j].p1 == edges[k].p2) && (edges[j].p2 == edges[k].p1))
        {
          edges[j].p1 = -1;
          edges[j].p2 = -1;
          edges[k].p1 = -1;
          edges[k].p2 = -1;
        }
        /* Shouldn't need the following, see note above */
        if ((edges[j].p1 == edges[k].p1) && (edges[j].p2 == edges[k].p2))
        {
          edges[j].p1 = -1;
          edges[j].p2 = -1;
          edges[k].p1 = -1;
          edges[k].p2 = -1;
        }
      }
    }
    /*
     Form new triangles for the current point
     Skipping over any tagged edges.
     All edges are arranged in clockwise order.
    */
    for (int j = 0; j < edges.size(); j++)
    {
      if (edges[j].p1 < 0 || edges[j].p2 < 0)
        continue;
      ITRIANGLE tmp;
      tmp.p1 = edges[j].p1;
      tmp.p2 = edges[j].p2;
      tmp.p3 = i;
      v.push_back(tmp);
      complete.push_back(false);
    }
  }
  /*
      Remove triangles with supertriangle vertices
      These are triangles which have a vertex number greater than nv
  */
  for (int i = 0; i < v.size(); i++)
  {
    if (v[i].p1 >= nv || v[i].p2 >= nv || v[i].p3 >= nv)
    {
      v[i] = v[v.size() - 1];
      v.pop_back();
      i--;
    }
  }
  pxyz.pop_back();
  pxyz.pop_back();
  pxyz.pop_back();
  return 0;
}

void randomize()
{
  srand((time_t)time(NULL));
}

int random(int n)
{
  return rand() % n;
}

bool cmp(XYZ &a, XYZ &b){
  if(a.x < b.x){
    return true;
  }else{
    return false;
  }
}

void outputtriangle(std::vector<XYZ> &pxyz, std::vector<ITRIANGLE> &v)
{
  std::ofstream off("triangle.off", std::ios::out);
  if (!off.good())
  {
    std::cerr << "Error: Could not open file "
              << "triangle.off"
              << " for writing!" << std::endl;
    off.close();
    return;
  }
  // write header
  off << "OFF" << std::endl;
  off << pxyz.size() << " " << v.size() << " 0" << std::endl;
  uint64_t n_vertices(pxyz.size());

  // write vertices
  for (u_int64_t v_it = 0; v_it < n_vertices; ++v_it)
  {
    off << pxyz[v_it].x << " " << pxyz[v_it].y << " " << pxyz[v_it].z << "\n";
  }
  // 清楚点数模式
  off.unsetf(std::ios::fixed);
  uint64_t n_faces(v.size());
  for (uint64_t c_it = 0; c_it < n_faces; ++c_it)
  {
    off << "3 ";
    off << v[c_it].p1 << " ";
    off << v[c_it].p2 << " ";
    off << v[c_it].p3 << " ";
    off << "\n";
  }
  off << "End\n";
  off.close();
  return;
}

/**
 * @description: 生成随机的点
 * @param {*}
 * @return {*}
 */
bool genPoints(std::vector<XYZ> &points, int numPoints){
  int nv = 0;
  bool b_Ok;
  double x, y;
  while(nv != numPoints){
    do{
      b_Ok = true;
      x = (double)random(500);
      y = (double)random(500);
      for (int n_Cpt = 0; n_Cpt < points.size(); n_Cpt++)
      {
        if ((x == points[n_Cpt].x) && (y == points[n_Cpt].y)){
          b_Ok = false;
        }
      } // to avoid similar points in the array
    }while (!b_Ok);
    nv++;
    XYZ tmp;
    tmp.x = x;
    tmp.y = y;
    tmp.z = 0;
    // 生成一个符合不重复的点
    points.push_back(tmp);
  }
  return true;
}

int main()
{
  std::vector<ITRIANGLE> vTriangle;
  std::vector<XYZ> points;
  double x, y, z;
  randomize();
  int n_MaxPoints = 10; // points size you want
  genPoints(points, n_MaxPoints);
  sort(points.begin(), points.end(), cmp);
  Triangulate(points, vTriangle);
  outputtriangle(points, vTriangle); // use this fonction to trace the mesh (via OpenGL, DirectX, ...)
  return 0;
}

小感悟

命运总是曲折离奇。我这个人有点难以专心看枯燥的东西，对着屏幕，对着ipad 还好一些，因为可以写写画画。

以后还是矩阵式学习，电脑代码，ipad思想草稿。

TIPS

QU: complete 有什么用?

AN: 在执行三角化之前用排序让所有的点沿着x 方向进行了排序，随着x增长，前面已近考虑了的且一定完备的三角形可以设定为true。

QU: 算法思想是什么简述：

AN:

http://paulbourke.net/papers/triangulate/ 这篇论文讲的很详细，先读懂论文，再看代码事半功倍。先看代码在看论文事倍功半。

subroutine triangulate
input : vertex list
output : triangle list
   initialize the triangle list
   determine the supertriangle
   add supertriangle vertices to the end of the vertex list
   add the supertriangle to the triangle list
   for each sample point in the vertex list
      initialize the edge buffer
      for each triangle currently in the triangle list
         calculate the triangle circumcircle center and radius
         if the point lies in the triangle circumcircle then
            add the three triangle edges to the edge buffer
            remove the triangle from the triangle list
         endif
      endfor
      delete all doubly specified edges from the edge buffer
         this leaves the edges of the enclosing polygon only
      add to the triangle list all triangles formed between the point
         and the edges of the enclosing polygon
   endfor
   remove any triangles from the triangle list that use the supertriangle vertices
   remove the supertriangle vertices from the vertex list
end

个人总结的思想：

Step 1：构建一个超级大的三角形，可以包含所有点的那种
Step 2: 将点按照某一维度排序，可以是x也可以是y
Step 3: 有一个三角形列表，超级大的三角形式第一个元素
-----
Step 4： 核心（可以读两遍）
现在我们要开始逐步加点了。
加入一个点，判断是否在所有的三角形列表中三角形的外接圆中，如果在三角形的外接圆中，将这个三角形的边加入“边临时数组”。将此三角形从三角形列表中删去。
对边临时数组进行遍历如果有同向或者反向的边，将其删除参考图1中的红色的线，因为红色的线是两个三角形共享的，所以会被删除。这样就剩下外围的包围框了是黑色厚的线条。
让所有的在边临时数组中的边和新加入的顶点相互连接构成新的三角形，并加入到三角形数组中。
如图2所示
-----
Step 5：去除三角形列表中和超级三角形有关的三角形。
Step 6: 删除掉点数组中关于超级三角形的点。
Step 7: 输出三角化网格

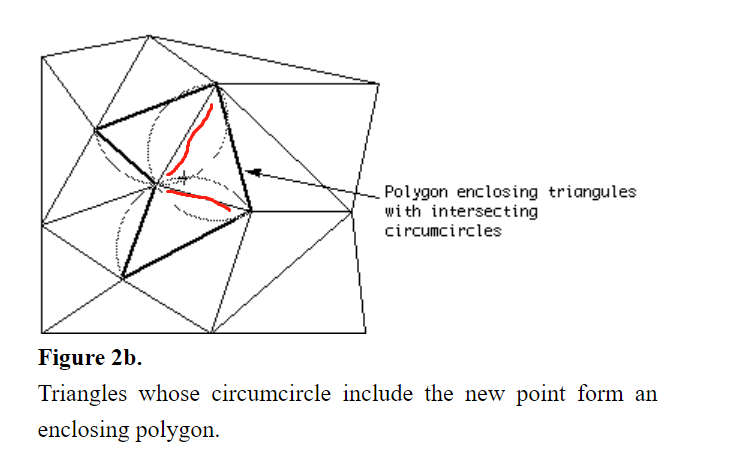
图1 上图

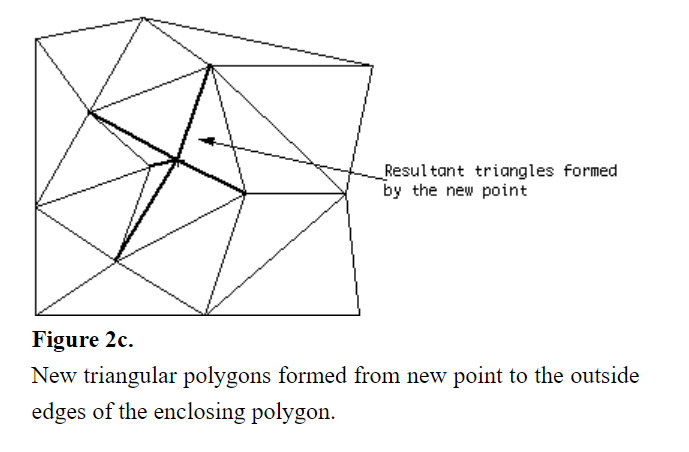
图2 上图

image

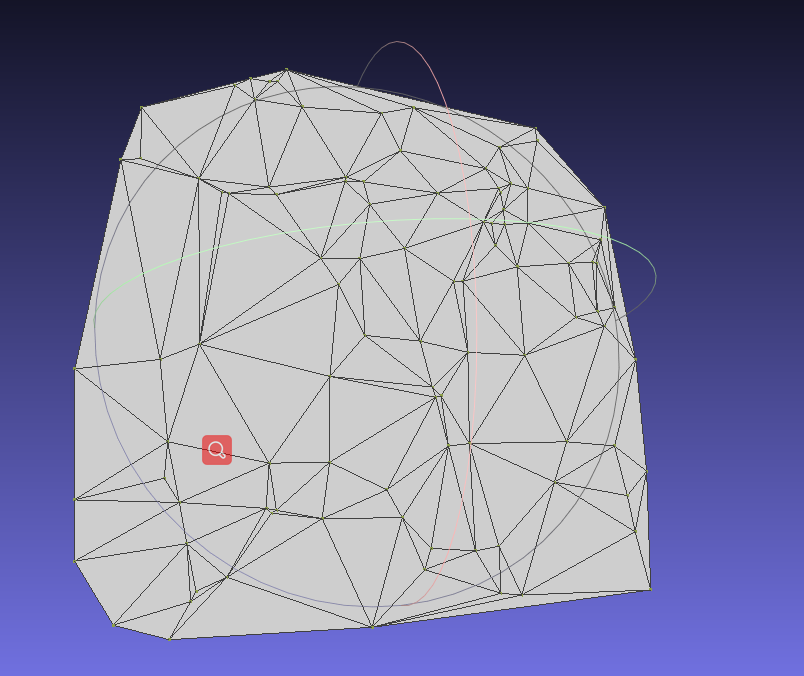
100个随机点生成的网格。因为改写了部分代码采用C++的STL可以更方便的构建更多点的方式。

1000个随机点生成的网格。很舒服。