KKRT-PSI
KKRT库:https://github.com/osu-crypto/BaRK-OPRF
文章:Efficient Batched Oblivious PRF with Applications to Private Set Intersection-2016
方案
解读论文,参考:Efficient Batched Oblivious PRF -Private Set Intersection
关键词:两方PSI、ORFT、OTE
引言
KKRT-PSI方案使用了OTE(OT扩展)、OPRF、Cuckoo哈希等技术,在大集合场景、局域网(带宽20GB/s)下运行效果最好。
方案构造思路:先设计一个OTE,进而设计一个OPRF,最后设计一个PSI
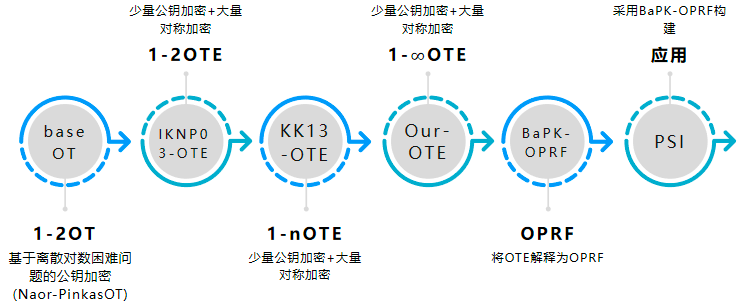
基础
1-2 OT
协议功能:Sender不知道Receiver的选择\(r\);Receiver只知道\(X_r\)
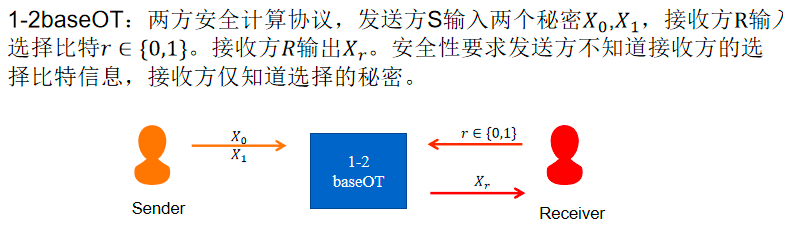
协议实现:有基于RSA的、基于DH的、基于ECC的等。
下面介绍的是Naor-Pinkas-OT,Naor和Pinkas通过三次公钥密码学操作实现了半诚实模型下的1-2 OT:
论文:Efficient oblivious transfer protocols-2001

其中\(E_{r,2}\)表示\(E_r\)的第二部分,若\(r=0\),则:

安全性:Sender根据\(PK_0\)不能反推出\(k\);Receiver根据\(g^a\)不能反推出\(a\)。
1-2 OTE
1-2 OT在实际应用中,每次都需使用一次,效率较低,所以下一步采用“固定数量的OT来实现任意数量的OT”,例如下图只需要使用\(k\)次1-2OT即可实现,其中\(k\)是根据安全参数决定的。
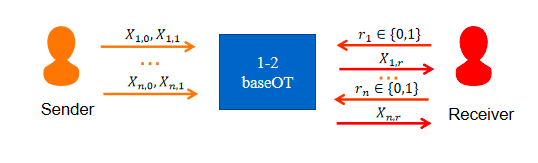
Ishai、Kilian、Nissim和Petrank于2003年提出基于矩阵变化实现少量1-2OT和对称密钥构造大量OT实例的不经意传输扩展协议。
论文:Extending Oblivious Transfers Efficiently-2003
本文提出了一种OT扩展协议,即\(k\)次1-2OT实现了\(m\)次1-OT,其中\(k<m\),,即每次有两种选择。文中给出了两种情况的协议:Receiver半诚实和Receiver恶意,下面介绍Receiver半诚实的协议:

分析:
注意:\(m_i\)表示列,\(m^i\)表示行
- 输入
- S:\(m\)对\((x_{j,0},x_{j,1})\),其中\(x_{j,b}\)是一个\(l\)bit的字符串
- R:选择比特\(r=(r_1,...,r_m)\in[0,1]\)
- 输出:
- R:得到\(m\)个\(x_{j,b}\)
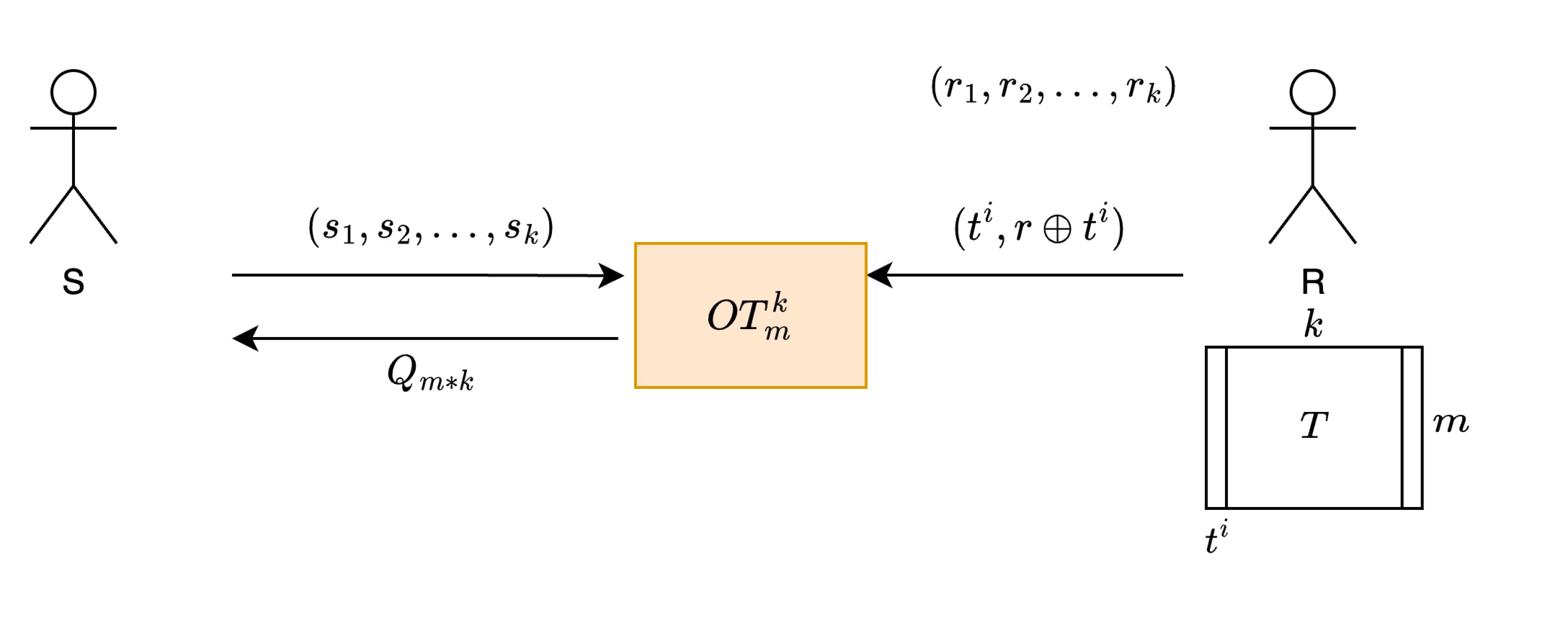
- 协议:
- 两方执行\(OT_m^k\)协议,S得到一个矩阵\(Q_{m*k}\),其中\(q^i=(s_i*r)\oplus t^i,i\in[1,k]\)(从列看)
- 从行看,\(q_j=(s*r_j)\oplus t_j=\left\{\begin{matrix}q_j=t_j,if(r_j=0)\\q_i=s\oplus t_j,if(r_j=1)\end{matrix}\right.,j\in[1,m]\)
- 从而有:\(t_j=q_j\oplus s\)
- S:对于每对\((x_{j,0},x_{j,1}),j\in[1,m]\),计算\(y_{j,0}=x_{j,0}\oplus H(j,q_j),y_{j,1}=x_{j,1}\oplus H(j,q_j\oplus s)\),并发送给R
- R:计算\(z_j=y_{j,r_j}\oplus H(j,t_j)\)
- 两方执行\(OT_m^k\)协议,S得到一个矩阵\(Q_{m*k}\),其中\(q^i=(s_i*r)\oplus t^i,i\in[1,k]\)(从列看)
- 正确性:

1-n OTE
IKN03方案是用\(k\)次OT实现了\(m\)次1-2OT,其中\(k<<m\)。KK13方案将IKN03中的\(r\)看作一个矩阵\(R_{m*k}\)(每列都一样),计算\(T=U \oplus R\),无需使用1-2OT实现1-nOT,仅改变了\(R\),利用编码技术,实现了\(1-n\)OTE。
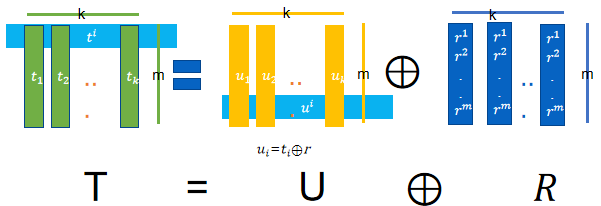
论文:Improved OT Extension for Transferring Short Secrets-2013
参考:KK13 OTE——Improved OT Extension for Transferring Short Secrets

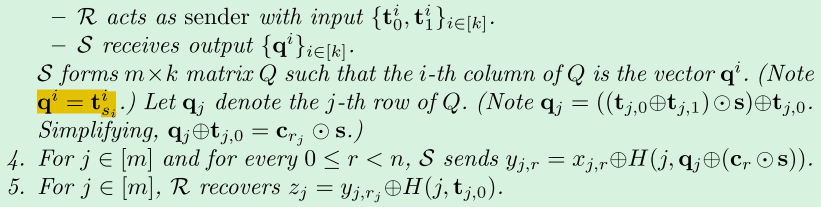
用\(k\)次1-n OT传递了\(m\)个信息,每个消息是\(lbit\),且是n个中选1个,其中\(k>=n\)。
- ️
- \(t_{j,0}\)表示矩阵\(T_0\)的第\(j\)行,有\(k\)个数据,每个数据为\(1bit\)。
- \(C_{WH}^k(a)\)表示输入一个\(log^k\)bit的字符串\(a\),输出一个\(k\)个字符串\((c_0,...,c_{k-1})\),每个字符串为\(kbit\),即可以看作是一个\(k*k\)的比特矩阵。
- 从行看,\(t_{j,0}\oplus t_{j,1}=c_{r_j}\),即\(T_1\)的行等于\(T_0\)的行和\(R\)中的行。
- S和R之间进行\(k\)次1-nOT,S获得了矩阵\(Q_{m*k}\)。
- 从列看,若\(s_i=0\),则\(q^i=t_0^i\);若\(s_i=1\),则\(q^i=t_1^i\),所以\(q^i=t_{s_i}^i\)。
- 从行看,\(q_j=((t_{j,0}\oplus t_{j,1})*s)\oplus t_{j,0} \to q_j=(c_{r_j}*s)\oplus t_{j,0}\)。

- 证明
- 最后S计算\(y_{j,r}\),共要计算\(m*n\)个,例如\(j=1\),则需发送\(y_{1,0},y_{1,1},...,y_{1,n-1}\),对于R来说,只取\(y_{1,1}\),其他无用。
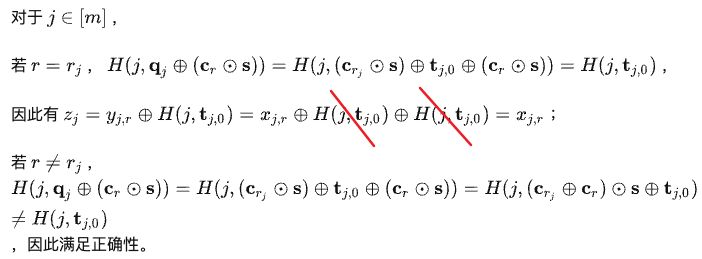
关于WH编码:
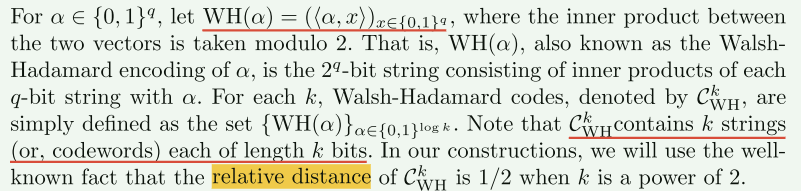
1-$\infty $ OTE
从KK13方案中,知道\(C_{WH}^k(a)\)是一种编码形式,即输入一个\(log^k\)bit的字符串\(a\),输出一个\(k\)个字符串\((c_0,...,c_{k-1})\),每个字符串为\(k\)bit,在进行隐私相等性测试时,即已知\(C_{WH}^k(a),C_{WH}^k(b)\),如何安全判断\(a\)和\(b\)是否相等,无需解码,只需比较\(C_{WH}^k(a),C_{WH}^k(b)\)是否相等即可,这里需要保证\(C_{WH}^k(a)\oplus C_{WH}^k(b)\)的汉明距离不小于计算安全参数。所以在KKRT16方案中的OTE,无需使用\(WH\)编码技术,只需要一个汉明距离不小于计算安全参数的伪随机函数即可。

BaRK-OPRF

- 首先介绍一下OPRF:
发送方和接收者执行两方OPRF协议,发送方无输入,接收方输入元素\(x_i\),发送方输出密钥\(k\),接收方输出OPRF值\(F(k,x_i)\):

- 下面介绍如何将KKRT16-OTE解释为一个OPRF协议:
上面提到需使用伪随机函数,这里伪随机函数的功能相当于KK13中的哈希,即\(F=H(j,\mathbf{q}_{j}\oplus(\mathbf{c}_{r}\odot\mathbf{s}))\)。一共有\(m\)个\(r_i\),可以执行\(m\)次OPRF。另外在2019年PRTY19和2020年CM20都基于第3个属性对OPRF协议进行了进一步的改进,得到多点OPRF,实现了正常带宽下最快的PSI协议。
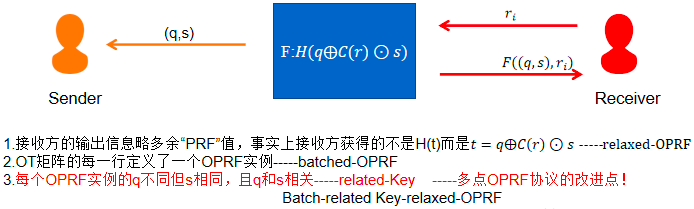
KKRT167中使用的OPRF由于是Batch、relaxed的,所以叫做BaRK-OPRF。
得到一个OPRF协议后,就可以很容易的构造一个PSI协议。例如下图:
- S与R执行OPRF,R输入隐私集合,输出OPRF值;
- S输出密钥\(k\),可计算任意的OPRF值,\(S\)本地计算OPRF值并将其发送给接收方,R通过字符串比较得到交集;
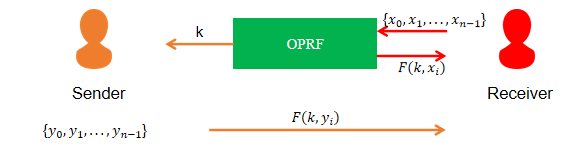
但接收方需要进行\(O(n^2)\)次比较。
Cuckoo 哈希
更多参考:https://www.cnblogs.com/pam-sh/p/16155650.html#cuckoo-hash
Cuckoo hashing分为两个存储表,一个为Cuchoo哈希表,一个称为堆存储容器。(本文协议采用的这样的容器,之后的文章有采用无堆存储容器的Cuckoo hashing)。
Cuckoo插入元素\(x\)的算法如下:
- 计算元素\(x\)的三个哈希值,寻找对应索引的位置,若至少有一个位置为空则随机插入空位置。若一个位置也没空,则随机选择一个位置替换该元素,然后对该元素执行上述步骤。
- 若执行\(k\)次后,仍然需要替换,则将该元素存储到堆存储器中!
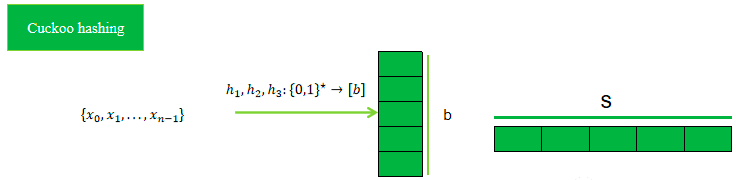
PSI协议
上述基于一个理想的OPRF构造了一个简单的PSI协议,但效率(计算和通信)较低。
KKRT16-PSI协议遵循了PSZZ15基于KK13-OTE构造PSI的思路,采用Cuckoo hashing算法减少了比较次数。对于128bit的字符串和足够大的集合,求交速度比PSZZ15快3.1~3.6倍,具体说只需3.8s就能求出集合大小为\(2^{20}\)的交集。
「PSZZ15」Phasing: Private set intersection using permutation-based hashing-2015
「PSZ14」Faster private set intersection based on OT extension-2014
总结了PSI协议构造的方法:基于哈希的、基于公钥加密的、基于GC的、基于OT的等。改进了「PSZ14」方案:使用置换哈希减少
bin的位长、使用哈希和安全电路计算,降低电路深度和通信消耗、使用改进的OT协议改进计算和内存消耗。
- 以PSSZ15的构造方式构造PSI协议,仅将OPRF协议替换为KKRT16-OTE
- 接收方随机选择3个hash函数,将集合元素通过布谷鸟hash算法映射到布谷鸟表或堆容器中,最后空余的地方采用虚拟元素填充;
- 发送方和接收方执行\((b+s)\)次OPRF实例,其中\(b\)和\(s\)分别代表布谷鸟表和堆容器的长度,并将OPRF值和元素\(x\)的对应存储位置联系起来;
- 发送方拥有密钥\(K\),本地计算H和S并将每一行打乱再发送给接收方;
- 接收方哈希表每一行的比较次数为3次,堆容器中的每个元素需要比较n次但只有s个元素且s为常量,因此只需要比较(3+s)n次;
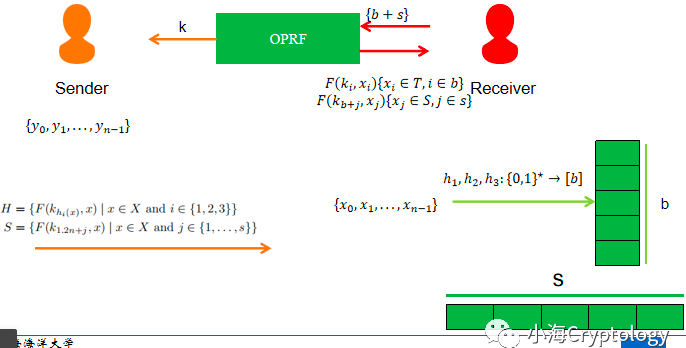
- 优化后,性能提升10%。
对于在bin中的数据,\(z\)表示所用的哈希函数,OPRF的输入为\(x||z\),输出为\(F(k_{h_z(x)},x||z)\);对于在stash中的数据,OPRF的输入不变,即\(x\),输出为\(F(k_{1.2n+x},x)\),所以H和S的生成为:\(\begin{gathered}
H_{i} =\{F(k_{h_t(x)},x\|i)\mid x\in X\},\text{for}i\in\{1,2,3\} \\
S_{j} =\{F(k_{1.2n+j},x)|x\in X\},\text{for}j\in\{1,\ldots,s\}
\end{gathered}\)。
这样PRF的值变为了\(n+ns\),且降低了OPRF的碰撞概率。
- 最后方案:

关于\(K=(k_1,....,k_{1.2n+s})\)的生成没有具体说,待补充。
论文







程序
编译安装
环境:Centos7.6
## 下载
git clone https://github.com/osu-crypto/BaRK-OPRF.git
## 下载依赖库
cd BaRK-OPRF/thirdparty
bash all_linux.get
## 会发现有些问题,需要将makelist中的'yum -Y'改为'yum -y'
## 编译
cd ..
make
## 会发现mpir安装的有问题,原来是给的下载链接失效了,重新找了一个替换上
## mpir.get文件
wget http://sources.buildroot.net/mpir/mpir-3.0.0.tar.bz2
tar -xjf mpir-3.0.0.tar.bz2
mv mpir-3.0.0 mpir
rm mpir-3.0.0.tar.bz2
cp ./mpir_patch/mpirxx.h ./mpir/
cp ./mpir_patch/mpir.h ./mpir/
cd mpir
./configure
make
## 重新编辑,即可
make
## 测试
./Release/bOPRFmain.exe -t
测试
单元测试
# 输入数据集规模为2^{12},进行测试
./Release/bOPRFmain.exe -t
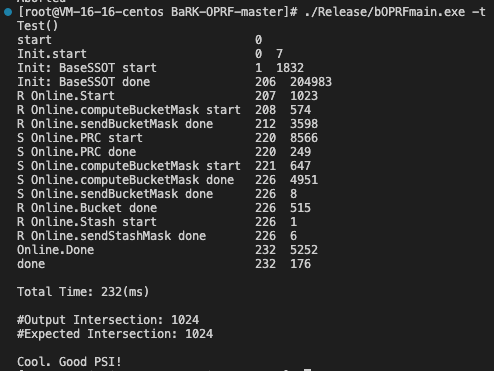
模拟测试
计算6种情况下的PSI,输入数据规模为(\(2^8\),\(2^{12}\),\(2^{16}\),\(2^{20}\),\(2^{24}\))。对于每种情况,运行代码10次来计算PSI。输出包括平均在线/离线/总运行时间(显示在屏幕上)和output.txt文件。
- 同机器
# Sener
./Release/bOPRFmain.exe -r 0
# Receiver
./Release/bOPRFmain.exe -r 1
- 不同机器
# Sener
./Release/bOPRFmain.exe -r 0 -ip <ipAdrress:portNumber>
# Receiver
./Release/bOPRFmain.exe -r 1 -ip <ipAdrress:portNumber>
解读
基础
- int main(int argc, char **argv)
//提示函数,其中argv0指向exe
void usage(const char *argv0)
{
std::cout << "Error! Please use:" << std::endl;
std::cout << "\t 1. For unit test: " << argv0 << " -t" << std::endl;
std::cout << "\t 2. For simulation (2 terminal): " << std::endl;
;
std::cout << "\t\t Sender terminal (localhost): " << argv0 << " -r 0" << std::endl;
std::cout << "\t\t Receiver terminal (localhost): " << argv0 << " -r 1" << std::endl;
std::cout << "\t\t Sender terminal (with ip input): " << argv0 << " -r 0 -ip <ip:port>" << std::endl;
std::cout << "\t\t Receiver terminal (with ip input): " << argv0 << " -r 1 -ip <ip:port>" << std::endl;
}
int main(int argc, char **argv)
{
//有两个参数,第一个为exe,第二个为“-t”,其中第二个参数argv[1][0] == '-',argv[1][1] == 't'
if (argc == 2 && argv[1][0] == '-' && argv[1][1] == 't')
{
BopTest();
}
//有三个参数,第一个为exe,第二个为“-r”,第三个为“0”,另外atoi()能把字符串转换成整型数
else if (argc == 3 && argv[1][0] == '-' && argv[1][1] == 'r' && atoi(argv[2]) == 0)
{
BopSender("localhost:1213");
}
//有三个参数,第一个为exe,第二个为“-r”,第三个为“1”
else if (argc == 3 && argv[1][0] == '-' && argv[1][1] == 'r' && atoi(argv[2]) == 1)
{
BopRecv("localhost:1213");
}
else if (argc == 5 && argv[1][0] == '-' && argv[1][1] == 'r' && atoi(argv[2]) == 0 && argv[3][0] == '-' && argv[3][1] == 'i' && argv[3][2] == 'p')
{
//获取ip
string ipAddr = argv[4];
BopSender(ipAddr);
}
else if (argc == 5 && argv[1][0] == '-' && argv[1][1] == 'r' && atoi(argv[2]) == 1 && argv[3][0] == '-' && argv[3][1] == 'i' && argv[3][2] == 'p')
{
string ipAddr = argv[4];
BopRecv(ipAddr);
}
else
{
//跳转提示
usage(argv[0]);
}
return 0;
}
int main(int argc, char** argv)主函数中的argc代表的是参数的数量,至少为1(argv[0]即.exe文件的路径)。argv为指针表示的参数,argv[0]表示第一个参数,argv[1]表示第二个参数,以此类推。
预处理
待补充
应用
隐语
参考:隐私集合求交
[KKRT16] 是半诚实 OT-based PSI协议,基于 OT Extension, BaRK-OPRF 和 CuckooHash。 [KKRT16] 是第一个在千万( 224224)规模,长度(128 bits)数据集上,求交时间在1分钟之内的PSI协议.
隐语 SPU PSI 中使用了 [PSZ18] 提到的 3-way stash-less CuckooHash:
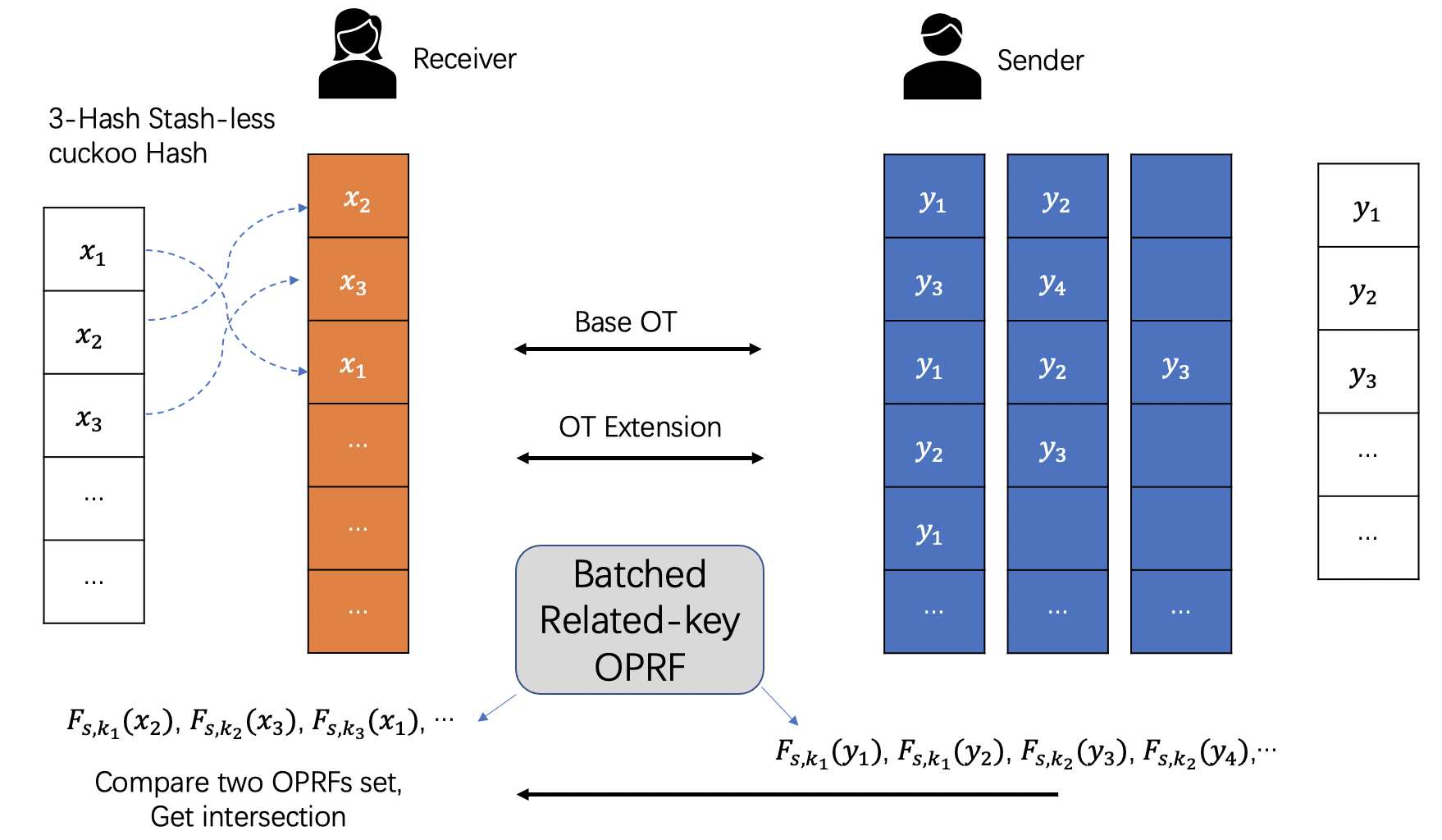

KKRT-PSI的更多相关文章
- PSI在windows server2008服务器上的安装方法
PSI(http://www.oschina.net/p/psi-crm)是一款开源进销存软件,功能较为齐全,使用比较方便.在windows server2008系统中安装时遇到了一些问题,总结解决方 ...
- 压力单位MPa、Psi和bar之间换算公式
压力单位MPa.Psi和bar之间换算公式 1bar=10^5PaPsi为英制压力单位.“磅力每平方英寸(1bf/in2)为1psi=6894.76 pa: 1bar等于10的5次方=10^5 pa ...
- PSi-Population Stability Index (PSI)
python信用评分卡(附代码,博主录制) https://study.163.com/course/introduction.htm?courseId=1005214003&utm_camp ...
- Psi Probe 安装及使用说明
这是一款 Tomcat 管理和监控工具,前身是 Lambda Probe.由于 Lambda Probe 2006不再更新,所以 PSI Probe 算是对其的一个 Fork 版本并一直更新至今. g ...
- 样本稳定指数PSI
信用评定等级划分之后需要对评级的划分做出评价,分析这样的评级划分结果是否具有实用价值,即分析样本分布的稳定程度.样本分布稳定,则信用评定等级划分结果的实用价值就高.采用样本稳定指数( PSI )检验样 ...
- PSI分析
"SI是对多个TS流的描述,它包含了PSI" PSI只提供了单个TS流的信息,使接收机能够对单个TS流中的不同节目进行解码:但是,它不能提供多个TS流的相关业务,也不能提供节目的类 ...
- 模型稳定度指标PSI与IV
由于模型是以特定时期的样本所开发的,此模型是否适用于开发样本之外的族群,必须经过稳定性测试才能得知.稳定度指标(population stability index ,PSI)可衡量测试样本及模型开发 ...
- Project Web Server PSI 接口一些常用操作
对Project Web Server进行二次开发,每天都把自己折腾到12点以后才休息,到处都是坑,研究那些烦人的PSI,国内根本查不到PSI相关的资料,对照API文档一点点谷歌资料,全部英文资料,开 ...
- PWA PSI statusingclient.UpdateStatus更新任务页面的AssnCustomFields的TextValue值
1.注意Changesxml格式和下面一定要一样 2.CustomFieldGuid和CustomFieldName都不能少,自定义域的uid和name其中uid或者是MD_PROP_UID_SECO ...
- IntelliJ IDEA 提交代码时出现:Code analysis failed with exception: com.intellij.psi......
IntelliJ IDEA 提交代码时出现:Code analysis failed with exception: com.intellij.psi...... 错误原因: 当我们勾选Perform ...
随机推荐
- 鸿蒙NEXT开发案例:计数器
[引言](完整代码在最后面) 本文将通过一个简单的计数器应用案例,介绍如何利用鸿蒙NEXT的特性开发高效.美观的应用程序.我们将涵盖计数器的基本功能实现.用户界面设计.数据持久化及动画效果的添加. [ ...
- 鸿蒙NEXT开发案例:血型遗传计算
[引言] 血型遗传计算器是一个帮助用户根据父母的血型预测子女可能的血型的应用.通过选择父母的血型,应用程序能够快速计算出孩子可能拥有的血型以及不可能拥有的血型.这个过程不仅涉及到了简单的数据处理逻辑, ...
- Python prometheus_client使用方式
#!/usr/bin/env python # -*- coding: utf8 -*- import socket,re from prometheus_client import generate ...
- Java线程池架构2-多线程调度器
http://ifeve.com/java线程池架构2-多线程调度器(scheduledthreadpoolexecutor)/ 在前面介绍了java的多线程的基本原理信息:<Java线程池 ...
- 轻量虚拟机之Multipass
官网:https://multipass.run/ 它可以快速在电脑上快速搭建一个轻量级的虚拟机,并且相比于 Vmware 更加轻量,只需一行命令快速创建 Ubuntu 虚拟机. Multipass ...
- fastadmin-表格使用
1.弹窗页面大小 <div id="toolbar" class="toolbar"> <a data-area='["90%&qu ...
- uni-app 使用笔记
1.前言 也不知道是我水平菜还是文档太烂,这个框架使用的过程中踩了无数的坑,屡次想砸键盘,最后贫穷让我平复了心情.为了纪念这段操蛋的日子,我决定把这些坑都记录下来. 2.数据请求 在实际的项目中,数据 ...
- 初识RPA以及简单的RPA项目——微信群发机器人
一.RPA的认识和理解 RPA(Robotic Process Automation)即是机器人流程自动化,简称RPA,是一种自动化技术,可以帮助组织实现业务流程的自动化执行,提高效率和准确性.按我的 ...
- 20号CSS学习
前面部分笔记丢失(呜呜有机会补) 一.盒子模型 1.4表格的细线边框 border-collapse: collapse;表示相邻边框合并在一起. 1.5边框会影响盒子的实际大小 测量时不测边框. 1 ...
- Vue项目报TypeError: Cannot read properties of undefined (reading '_wrapper')
前情 最近在做一个营销活动的时候,我选择了Vue技术栈来开发. 坑位 项目看似一切都正常,但当我在绑定的js事件中去修改当前组件的data上的值时会报错:TypeError: Cannot read ...
