图论 I

进军图论！

本篇图论主要内容：最短路、最小生成树。

定义与记号

涉及常见或可能用到的概念的定义。关于更多，见参考资料。

基本定义

• 图：一张图 \(G\) 由若干个点和连接这些点的边构成。点的集合称为 点集 \(V\)，边的集合称为 边集 \(E\)，记 \(G = (V, E)\)。
• 阶：图 \(G\) 的点数 \(|V|\) 称为 阶，记作 \(|G|\)。
• 无向图：若 \(e\in E\) 没有方向，则 \(G\) 称为 无向图。无向图的边记作 \(e = (u, v)\)，\(u, v\) 之间无序。
• 有向图：若 \(e\in E\) 有方向，则 \(G\) 称为 有向图。有向图的边记作 \(e = u\to v\) 或 \(e = (u, v)\)，\(u, v\) 之间有序。无向边 \((u, v)\) 可视为两条有向边 \(u\to v\) 和 \(v\to u\)。
• 重边：端点和方向（有向图）相同的边称为 重边。
• 自环：连接相同点的边称为 自环。

相邻

• 相邻：在无向图中，称 \(u, v\) 相邻 当且仅当存在 \(e = (u, v)\)。
• 邻域：在无向图中，点 \(u\) 的 邻域 为所有与之相邻的点的集合，记作 \(N(u)\)。
• 邻边：在无向图中，与 \(u\) 相连的边 \((u, v)\) 称为 \(u\) 的 邻边。
• 出边 / 入边：在有向图中，从 \(u\) 出发的边 \(u\to v\) 称为 \(u\) 的 出边，到达 \(u\) 的边 \(v\to u\) 称为 \(u\) 的 入边。
• 度数：一个点的 度数 为与之关联的边的数量，记作 \(d(u)\)，\(d(u) = \sum_{e\in E} ([u = e_u] + [u = e_v])\)。点的自环对其度数产生 \(2\) 的贡献。
• 出度 / 入度：在有向图中，从 \(u\) 出发的边数称为 \(u\) 的 出度，记作 \(d ^ +(u)\)；到达 \(u\) 的边数称为 \(u\) 的 入度，记作 \(d ^ -(u)\)。

路径

• 途径：连接一串相邻结点的序列称为 途径，用点序列 \(v_{0..k}\) 和边序列 \(e_{1..k}\) 描述，其中 \(e_i = (v_{i - 1}, v_i)\)。常写为 \(v_0\to v_1\to \cdots \to v_k\)。
• 迹：不经过重复边的途径称为 迹。
• 回路：\(v_0 = v_k\) 的迹称为 回路。
• 路径：不经过重复点的迹称为 路径，也称 简单路径。不经过重复点比不经过重复边强，所以不经过重复点的途径也是路径。注意题目中的简单路径可能指迹。
• 环：除 \(v_0 = v_k\) 外所有点互不相同的途径称为 环，也称 圈 或 简单环。

连通性

• 连通：对于无向图的两点 \(u, v\)，若存在途径使得 \(v_0 = u\) 且 \(v_k = v\)，则称 \(u, v\) 连通。
• 弱连通：对于有向图的两点 \(u, v\)，若将有向边改为无向边后 \(u, v\) 连通，则称 \(u, v\) 弱连通。
• 连通图：任意两点连通的无向图称为 连通图。
• 弱连通图：任意两点弱连通的有向图称为 弱连通图。
• 可达：对于有向图的两点 \(u, v\)，若存在途径使得 \(v_0 = u\) 且 \(v_k = v\)，则称 \(u\) 可达 \(v\)，记作 \(u \rightsquigarrow v\)。
• 关于点双连通 / 边双连通 / 强连通，见对应章节。

特殊图

• 简单图：不含重边和自环的图称为 简单图。
• 基图：将有向图的有向边替换为无向边得到的图称为该有向图的 基图。
• 有向无环图：不含环的有向图称为 有向无环图，简称 DAG（Directed Acyclic Graph）。
• 完全图：任意不同的两点之间恰有一条边的无向简单图称为 完全图。\(n\) 阶完全图记作 \(K_n\)。
• 树：不含环的无向连通图称为 树，树上度为 \(1\) 的点称为 叶子。树是简单图，满足 \(|V| = |E| + 1\)。若干棵（包括一棵）树组成的连通块称为 森林。相关知识点见 “树论”。
• 稀疏图 / 稠密图： \(|E|\) 远小于 \(|V| ^ 2\) 的图称为 稀疏图，\(|E|\) 接近 \(|V| ^ 2\) 的图称为 稠密图。用于讨论时间复杂度为 \(\mathcal{O}(|E|)\) 和 \(\mathcal{O}(|V| ^ 2)\) 的算法。

子图

• 子图：满足 \(V'\subseteq V\) 且 \(E'\subseteq E\) 的图 \(G' = (V', E')\) 称为 \(G = (V, E)\) 的 子图，记作 \(G'\subseteq G\)。要求 \(E'\) 所有边的两端均在 \(V'\) 中。
• 导出子图：选择若干个点以及两端都在该点集的所有边构成的子图称为该图的 导出子图。导出子图的形态仅由选择的点集 \(V'\) 决定，记作 \(G[V']\)。
• 生成子图：\(|V'| = |V|\) 的子图称为 生成子图。
• 极大子图（分量）：在子图满足某性质的前提下，子图 \(G'\) 称为 极大 的，当且仅当不存在同样满足该性质的子图 \(G''\) 且 \(G'\subsetneq G''\subseteq G\)。\(G'\) 称为满足该性质的 分量。例如，极大的连通的子图称为原图的连通分量，也就是我们熟知的连通块。

约定

• 记 \(n\) 表示点集大小 \(|V|\)，\(m\) 表示边集大小 \(|E|\)。

前置东西

宽度优先搜索（BFS），深度优先搜索（DFS），一个脑子，一个电脑，两只手。

拓扑排序及其应用

对 DAG 进行拓扑排序，得到结点序列 \(\{p_i\}\)，满足图上每条边的起始点比终点在序列上更靠前。形式化地，设 \(q_i\) 表示结点 \(i\) 在 \(p\) 中的位置，那么对于图上每条边 \(u\to v\)，均有 \(q_u < q_v\)。

每次取入度为 \(0\) 的点 \(u\) 加入 \(p\)，将从 \(u\) 出发的所有边删去。因为一条边被删去时，其起始点已经加入序列，而终点没有加入序列（入度大于 \(0\)），所以起始点相较终点在序列上更靠前。

拓扑排序没有结束时，必然存在入度为 \(0\) 的点。否则，从剩下的图上任意一点出发走每个点的第一条出边得到无限长的点序列。因为结点数有限，所以序列一定经过了重复的点，与原图无环矛盾。

通过 BFS 或 DFS 实现拓扑排序：

• BFS：用队列维护所有入度为 \(0\) 的点。取出队首 \(u\)，删去从 \(u\) 出发的所有边 \(u\to v\)。如果删边导致某个点 \(v\) 从入度大于 \(0\) 变成入度等于 \(0\)，那么将 \(v\) 入队。初始将所有入度为 \(0\) 的点入队。
• DFS：对于当前点 \(u\)，若 \(v\) 在删去 \(u\to v\) 后从入度大于 \(0\) 变成入度等于 \(0\)，那么向 \(v\) DFS。初始从每个入度为 \(0\) 的点开始搜索。

时间复杂度为 \(\mathcal{O}(n + m)\)。

模板题 代码。

// Problem: B3644 【模板】拓扑排序 / 家谱树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/B3644
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
#define endl '\n'
#define pi pair<int, int>
// #define int long long
// #pragma GCC optimize(2)

using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int n, d[N];
queue<int> q;

int pre[N], k;
struct node {
    int to, next;
} a[N];

inline void add(int u, int v) {
    a[++k] = {v, pre[u]};
    pre[u] = k;
    return;
}

inline int read() {
    int x;
    cin >> x;
    return x;
}

inline void toposort() {
    for (int i = 1; i <= n; i++)
        if (!d[i]) q.push(i);
    while (q.size()) {
        int t = q.front();
        cout << t << " ";
        q.pop();
        for (int i = pre[t]; i; i = a[i].next) {
            int to = a[i].to;
            if (--d[to] == 0) q.push(to);
        }
    }
    return;
}

signed main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    n = read();
    for (int i = 1, x; i <= n; i++) {
        while (x = read()) {
            if (!x) break;
            add(i, x);
            d[x]++;
        }
    }
    toposort();
    return 0;
}

拓扑序常用于解决建图题或图论类型的构造题。

拓扑序不唯一，例如图 \((1\to 2, 1\to 3)\) 有两个拓扑序 \(\{1, 2, 3\}\) 和 \(\{1, 3, 2\}\)。除非有特殊性质，拓扑序计数无法做到多项式复杂度。

拓扑排序衍生出的各种问题：

• 拓扑序 DP，即在拓扑序上通过 DP 的方式统计答案（补：拓扑序的性质对应 DP 的无后效性）。
  • DAG 最长路。设 \(f_i\) 表示以 \(i\) 结尾的最长路径长度，按拓扑序转移：\(f_v\gets \max(f_v, f_u + 1)\)。例题：P1137，P3573（第一章例题），P3387（4.3 小节的模板题）。
  • DAG 路径计数。设 \(f_i\) 表示以 \(i\) 结尾的路径条数，按拓扑序转移：\(f_v\gets f_v + f_u\)。例题：P3183，P4017。
  • 点对可达性统计。设 \(f_{i, j}\) 表示 \(i\) 是否可达 \(j\)，按拓扑序转移：\(f_{v, j}\gets f_{v, j}\lor f_{u, j}\)，用 bitset 优化，时间复杂度 \(\mathcal{O}(\frac {|V||E|}{w})\)。例题：P7877（“建图相关” 例题）
• 最小 / 最大字典序拓扑序：在 BFS 求拓扑序时，将队列换成优先队列。可归纳证明每一步都取到了字典序最小值。例题：P3243，CF1765H。
• 树拓扑序计数，拓扑序容斥：见 “计数 DP”。
• 结合有向图强连通分量缩点，缩点后拓扑排序，解决一般有向图上的问题。

无向图 DFS 树

给定无向连通图 \(G\)，从点 \(r\) 开始 DFS，取出进入每个点 \(i\) 时对应的边 \((fa_i, i)\) 并定向为 \(fa_i\to i\)，得到以 \(r\) 为根的有向树。称 \((fa_i, i)\) 为 树边，其它边为 非树边。

给每个点标号为它被访问到的次序，称为 时间戳，简称 dfn。按 DFS 的访问顺序得到的结点序列称为 DFS 序，或称重编号，时间戳为 \(i\) 的结点在 DFS 序上的位置为 \(i\)。

Graph editor 功能有待提升。

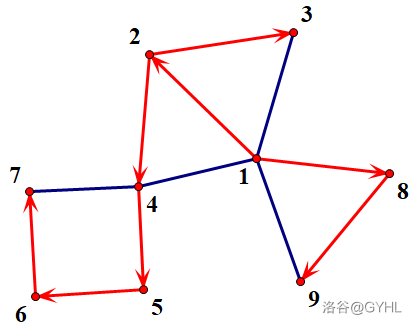
上图是一个可能的 DFS 树以及对应的时间戳。

无向图 DFS 树的性质：

• 祖先后代性：任意非树边两端具有祖先后代关系。
• 子树独立性：结点的每个儿子的子树之间没有边（和上一条性质等价）。
• 时间戳区间性：子树时间戳为一段区间。
• 时间戳单调性：结点的时间戳小于其子树内结点的时间戳。

正确性留给读者思考。

关于有向图 DFS 树，见第四章。

1. 最短路及其应用

最短路是图论的一类经典问题。最优化 DP 在有环的图上转移就是最短路。

1.1 相关定义

在研究最短路问题（Shortest Path Problem，SPP）时，研究对象是路径而非途径，因为总可以钦定两点之间的最短路不经过重复点，否则起点和终点之间存在负环，最短路不存在。

• 带权图：每条边带有权值的图称为 带权图（赋权图）。所有边的权值非负的图称为 非负权图；所有边的权值为正的图称为 正权图。
• 边权：边的权值称为 边权，记作 \(w_e\) 或 \(w_{u, v}\)。带权边记作 \((u, v, w)\)。若边不带权，默认边权为 \(1\)。
• 路径长度：路径上每条边的权值之和称为 路径长度。
• 负环：长度为负数的环称为 负环。
• 最短路：在一张图上，称 \(s\) 到 \(t\) 的 最短路 为最短的连接 \(s\) 到 \(t\) 的路径。若不存在这样的路径（不连通或不可达），或最小值不存在（存在可经过的负环），则最短路不存在。
• 记 \(s\) 表示最短路起点，\(t\) 表示最短路终点。

1.2 单源最短路径问题

问题描述：给定 源点 \(s\)，求 \(s\) 到图上每个点 \(u\) 的最短路长度 \(D_u\)。

设 \(dis_u\) 表示 \(s\) 到 \(u\) 的估计最短路长度，初始化 \(dis_s = 0\) 和 \(dis_u = +\infty\)（\(u\neq s\)），算法结束时应有 \(dis_u = D_u\)。

接下来介绍该问题的几种常见解法。

1.2.1 Bellman-Ford

Bellman-Ford 是一种暴力求解单源最短路径的方法。

称一轮 松弛 表示对每条边 \((u, v)\)，用 \(dis_u + w_{u, v}\) 更新 \(dis_v\)。松弛 \(n - 1\) 轮即可。

证明

在 \(s\rightsquigarrow u\) 的最短路 \(s\to p_1\to\cdots\to u\) 中，对于每个点 \(p_i\)，\(s\to p_1\to\cdots\to p_i\) 一定是 \(s\rightsquigarrow p_i\) 的最短路。这说明一个点的最短路由另一个点的最短路扩展而来。

因为最短路至多有 \(n - 1\) 条边，而第 \(i\) 轮松弛会得到边数为 \(i\) 的最短路，故只需松弛 \(n - 1\) 轮。

该算法可以判断一张图上是否存在负环：若第 \(n\) 轮松弛时仍有结点的最短路被更新，则图上存在负环。

算法的时间复杂度为 \(\mathcal{O}(nm)\)。

1.2.2 Dijkstra

Dijkstra 算法适用于 非负权图。网上的一些博客认为 Dijkstra 使用了贪心思想。

称 扩展 结点 \(u\) 表示对 \(u\) 的所有邻边 \((u, v)\)，用 \(dis_u + w_{u, v}\) 更新 \(dis_v\)。

在 \(dis_u = D_u\) 的结点中，取出 \(dis\) 最小且未扩展过的点并扩展。因为没有负权边，所以取出结点的最短路长度单调不降。

如何判断一个点的 \(dis_u\) 已经等于 \(D_u\)？实际上，当前 \(dis\) 最小且未扩展过的点一定满足 \(dis_u = D_u\)。

证明

归纳假设已经扩展过的结点 \(p_1, p_2, \cdots, p_{k - 1}\) 在扩展时取到了最短路。\(p_k\) 为未扩展的 \(dis\) 最小的结点。

\(p_k\) 的最短路一定由 \(p_i\)（\(1\leq i < k\)）的最短路扩展而来，不可能出现

\[dis(p_i) + w(p_i, u_1) + w(u_1, u_2) + \cdots + w(u_c, p_k) < dis(p_j) + w(p_j, p_k)
\]

的情况，其中 \(u_{1\sim c}\) 均未扩展。否则由于边权非负，\(dis(p_i) + w(p_i, u_1) < dis(p_j) + w(p_j, p_k)\)，即当前 \(dis(u_1) < dis(p_k)\)，与 \(dis(p_k)\) 的最小性矛盾。

初始令源点的 \(dis\) 为 \(0\)，假设成立，算法正确。

简单地说，一个点的最短路由长度非严格更小的最短路更新得到，\(dis\) 最小的结点一定不会被其它结点更新。

取出 \(dis\) 最小的结点可用优先队列维护。扩展 \(u\) 时，若 \(dis_u + w_{u, v} < dis_v\)，那么将 \((v, dis_u + w_{u, v})\) 即结点编号和它更新后的 \(dis\) 作为二元组丢进优先队列。尝试取出结点时，以 \(dis_u + w_{u, v}\) 为关键字取出最小的二元组，扩展该二元组对应的结点。

注意，一个结点可能有多个入边并多次进入优先队列，但当它第一次被取出时，对应的 \(dis\) 一定为最短路。为此，需判断是否有第二元（距离）等于第一元（编号）的 \(dis\)。若不等，说明该点已扩展过，直接跳过，否则复杂度将退化为 \(\mathcal{O}(m ^ 2\log m)\)。

算法的时间复杂度为 \(\mathcal{O}(m\log m)\)。当图为稠密图（\(m\) 接近 \(n ^ 2\)）时，用暴力代替优先队列，时间复杂度 \(\mathcal{O}(n ^ 2)\)。

扩展：当边权只有 \(0\) 和 \(1\) 时，使用双端队列代替优先队列：成功扩展权值为 \(0\) 的出边时压入队首，成功扩展权值为 \(1\) 的出边时压入队尾。称为 01 BFS。

模板题 代码。

// Problem: P4779 【模板】单源最短路径（标准版）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4779
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
#define endl '\n'
#define pi pair<int, int>
// #define int long long
// #pragma GCC optimize(2)

using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 1e5 + 10, M = 2e5 + 10;
int n, m, start, d[N];
bool f[N];

int pre[N], k;
struct node {
    int to, next, len;
} a[M];

inline void add(int u, int v, int l) {
    a[++k] = {v, pre[u], l};
    pre[u] = k;
    return;
}

inline int read() {
    int x;
    cin >> x;
    return x;
}

inline void dijkstra(int start) {
    priority_queue<pi, vector<pi>, greater<pi>> q;
    q.push({0, start});
    memset(d, 0x3f, sizeof d);
    memset(f, false, sizeof f);
    d[start] = 0;
    while (q.size()) {
        auto [dis, x] = q.top();
        q.pop();
        if (f[x]) continue;
        f[x] = true;
        for (int i = pre[x]; i; i = a[i].next) {
            int to = a[i].to;
            if (d[x] + a[i].len < d[to]) {
                d[to] = d[x] + a[i].len;
                if (!f[to]) q.push({d[to], to});
            }
        }
    }
    return;
}

signed main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    n = read(), m = read(), start = read();
    for (int i = 1; i <= m; i++) {
        int u = read(), v = read(), l = read();
        add(u, v, l);
    }
    dijkstra(start);
    for (int i = 1; i <= n; i++) cout << d[i] << " ";
    return 0;
}

1.2.3 SPFA 与负环

关于 SPFA，___。

SPFA（Shortest Path Faster Algorithm）是队列优化的 Bellman-Ford。

松弛点 \(x\) 时找到接下来可能松弛的点，即与 \(x\) 相邻且 最短路被更新的点 并压入队列。此外，记录一个点是否在队列中，若是，则不压入，可以显著减小常数。

时间复杂度相比 BF 并没有改进，仍为 \(\mathcal{O}(nm)\)。在一般图上效率很高，但可以被特殊数据卡成平方，所以能用 Dijkstra（非负权图）时不建议 SPFA。

注意：若使用 SPFA 求解点对点的最短路径，如费用流 EK，当队头为目标结点时不能结束算法。因为一个点进入队列并不代表其 \(dis\) 已经取到了最短路长度。

SPFA 判负环：若一个点 进入队列 超过 \(n - 1\) 次（不是被松弛，因为一个点被松弛不一定进入队列），或 最短路边数 大于 \(n - 1\)，则整张图存在 从源点可达 的负环。对于后者，记录 \(l_i\) 表示从源点到 \(i\) 的最短路长度，松弛时令 \(l_v\gets l_u + 1\) 并判断是否有 \(l_v < n\)。

一般判入队次数慢于最短路长度，推荐使用后者。

模板题 代码。

// Problem: P3385 【模板】负环
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3385
// Memory Limit: 250 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
#define endl '\n'

using namespace std;
const int N = 2e3 + 10, M = 6e3 + 10;
int n, m;
int dis[N], vis[N], cnt[N];
queue<int> q;

int pre[N], k;
struct node {
    int to, next, w;
} a[M];

inline int read(){
	int x;
	cin>>x;
	return x;
}

inline void init() {
    memset(pre, 0, sizeof pre);
    memset(dis, 0x3f, sizeof dis);
    memset(vis, 0, sizeof vis);
    memset(cnt, 0, sizeof cnt);
    k = 0;
    return;
}

inline void add(int u, int v, int w) {
    a[++k] = {v, pre[u], w};
    pre[u] = k;
    return;
}

inline bool spfa() {
    dis[1] = 0;
    vis[1] = true;
    q.push(1);
    while (!q.empty()) {
        int x = q.front();
        q.pop();
        vis[x] = false;
        for (int i = pre[x]; i; i = a[i].next) {
            int y = a[i].to, z = a[i].w;
            if (dis[y] > dis[x] + z) {
                dis[y] = dis[x] + z;
                cnt[y] = cnt[x] + 1;
                if (cnt[y] >= n) return true;
                if (!vis[y]) {
                    q.push(y);
                    vis[y] = true;
                }
            }
        }
    }
    return false;
}

inline void solve() {
    init();
    cin >> n >> m;
    for (int i = 1, u, v, w; i <= m; i++) {
        cin >> u >> v >> w;
        add(u, v, w);
        if (w >= 0) add(v, u, w);
    }
    cout << (spfa() ? "YES\n" : "NO\n");
    return;
}

signed main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int _ = read();
    while (_--) solve();
    return 0;
}

1.2.4 三角形不等式

在单源最短路径问题中，对于每条边 \((u, v)\in E\)，有 \(D_u + w_{u, v} \geq D_v\)，称为 三角形不等式。

三角形不等式是每个点的单源最短路径长度满足的性质。相反，给出若干条三角形不等式的限制，求能否找到一组满足条件的解，就是经典的 差分约束 问题。

1.3 差分约束问题

问题描述：给定若干形如 \(x_a-x_b\leq c\) 或 \(x_a - x_b \geq c\) 的不等式限制，求任意一组解 \(\{x_i\}\)。

1.3.1 算法介绍

只要 \(x_a, x_b\) 在不等号同一侧时符号不同，那么所有限制均可写为 \(x_i + c \geq x_j\)。

通过单源最短路径求出的 \(dis\) 满足三角形不等式，每条边对应一个不等式。这启发我们将给出的不等式还原成边，在建出的图上跑单源最短路径。

从 \(i\to j\) 连长度为 \(c\) 的边，再从超级源点 \(0\) 向每个点连长度为 \(0\) 的边防止图不连通，或初始令所有 \(dis = 0\) 并将所有点入队，每个点的最短路长度就是一组解。

因为 \(c\) 可能为负值（若 \(c\) 非负，令所有 \(x\) 相等即可），所以使用 Bellman-Ford 或 SPFA 求解最短路。若出现负环则无解，这说明不等式要求一个数加上负数后不小于其本身。

时间复杂度 \(\mathcal{O}(nm)\)。

模板题 代码。

// Problem: P5960 【模板】差分约束
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5960
// Memory Limit: 128 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)

/*+ Nimbunny +*/

#include <bits/stdc++.h>
#define endl '\n'
#define pi pair<int, int>
// #define int long long
// #pragma GCC optimize(2)

using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 5e3 + 10;
int n, m, dis[N], len[N];
bool vis[N];
vector<pi> e[N];

inline int read() {
    int x;
    cin >> x;
    return x;
}

inline void solve() {
    n = read(), m = read();
    for (int i = 1; i <= m; i++) {
        int u = read(), v = read();
        e[v].push_back(make_pair(u, read()));
    }
    queue<int> q;
    for (int i = 1; i <= n; i++) q.push(i), vis[i] = true;
    while (!q.empty()) {
        int t = q.front();
        q.pop(), vis[t] = false;
        for (auto it : e[t]) {
            int to = it.first, d = dis[t] + it.second;
            if (d < dis[to]) {
                dis[to] = d, len[to] = len[t] + 1;
                if (len[to] == n) return cout << "NO\n", void();
                if (!vis[to]) q.push(to), vis[to] = true;
            }
        }
    }
    for (int i = 1; i <= n; i++) cout << dis[i] << " ";
    return;
}

signed main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int _ = 1;
    while (_--) solve();
    return 0;
}

例题：P4926，P5590，P3530。

1.3.2 解的字典序极值

一般而言差分约束系统的解没有 “字典序极值” 这个概念，因为我们只对变量之间的差值进行约束，而变量本身的值随着某个变量取值的固定而固定。

字典序的极值建立于变量有界的基础上。不妨设希望求出当限制 \(x_i\leq 0\) 时，整个差分约束系统的字典序的最大值。注意到 \(x_i \leq 0\) 可以看成三角形不等式 \((x_0 = 0) + 0 \geq x_i\)，所以我们建立虚点 \(0\)，将其初始 \(dis\) 赋为 \(0\)，并向其它所有变量连权值为 \(0\) 的边（等价于初始令所有点入队且 \(dis = 0\)）。

求解差分约束系统时我们使用了三角形不等式，将其转化为最短路问题。这给予它很好的性质：通过 SPFA 求得的解恰为字典序最大解。

对于一条 \(u\to v\) 的边权为 \(w(u, v)\) 的边，它的含义为限制 \(x_u + w(u, v) \geq x_v\)。

考虑 \(0\) 到 \(i\) 的最短路。因为最短路上的所有边均有 \(x_u + w(u, v) = x_v\)，所以如果将 \(x_i\) 增大 \(1\)，那么最短路上至少有一条边的限制无法被满足。这说明每个变量都取到了其上界，自然满足字典序最大。

对于字典序最小解，限制 \(x_i \geq 0\)。所有结点向 \(0\) 连边 \(w(i, 0) = 0\)。字典序最小即字典序最大时的相反数。因此，考虑将所有变量取反，那么限制也要全部取反，体现为将图中所有边（包括所有新建的边 \(i\to 0\)）的 方向（而不是边权）取反：\(-x_u + w(u, v) \geq -x_v \implies x_v + w(u, v) \geq x_u\)。然后求字典序最大解，再取相反数即可。

1.4 全源最短路径问题

问题描述：求任意两点之间的最短路 \(D_{s, t}\)。注意有向图中 \(s, t\) 有序。

1.4.1 Johnson

前置知识：Bellman-Ford，Dijkstra。

Johnson 算法用于解决 带有负权边 的全源最短路径问题。

Johnson 算法的巧妙之处在于为每个点赋予 势能 \(h_i\)。貌似正如物理意义上的势能，从一个点出发到达另一个点，无论走什么路径，势能的总变化量是一定的。这启发我们将边 \((u, v)\) 的新权值 \(w'_{u, v}\) 设置为 \(w_{u, v} + h_u - h_v\)。

考虑路径 \(S\to p_1 \to p_2 \to \cdots \to T\)，原长度为

\[L(S\rightsquigarrow T) = w_{S, p_1} + w_{p_1, p_2} + \cdots + w_{p_l, T}
\]

新长度为

\[L'(S\rightsquigarrow T) = (h_S + w_{S, p_1} - h_{p_1}) + (h_{p_1} + w_{p_1, p_2} - h_{p_2}) + \cdots + (h_{p_l} + w_{p_l, T} - h_T)
\]

则 \(L(S\rightsquigarrow T) = L'(S\rightsquigarrow T) + h_T - h_S\)。

对于固定的 \(S, T\)，原图的路径对应到新图上面，长度增加了 \(h_S - h_T\)。这与路径经过了哪些点无关，只与 \(S, T\) 有关。因此，原图 \(S\rightsquigarrow T\) 的最短路在新图上仍为最短路。

由于负权，我们无法使用 Dijkstra 求解最短路。多次 Bellman-Ford 或 SPFA 的时间复杂度不优秀。尝试应用上述分析，合理地为每个点赋权值，从而消去图上的所有负权边。

为使 \(w'(u, v) \geq 0\)，只需 \(w(u, v) + h_u \geq h_v\)，求解差分约束即可：若初始图中无负环，则 \(h\) 一定存在。令所有 \(h\) 等于 \(0\)，然后使用 Bellman-Ford 进行 \(n - 1\) 轮松弛。松弛在 \(n - 1\) 轮后必然结束，否则原图存在负环。

操作结束后，更新每条边的权值 \(w'(u, v) = w(u, v) + h_u - h_v\)。根据一开始的分析，得到的新图与原图任意两点最短路经过的结点不变，且无负边权，可以使用 \(n\) 轮 Dijkstra 求解。

最后不要忘了将 \(u\rightsquigarrow v\) 的最短路加上 \(h_v - h_u\)。

算法的时间复杂度为 \(\mathcal{O}(nm\log m)\)。

模板题 代码。

// Problem: P5905 【模板】全源最短路（Johnson）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5905
// Memory Limit: 128 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)

/*+ Nimbunny +*/

#include <bits/stdc++.h>
#define int long long
#define pi pair<int, int>

using namespace std;
const int N = 3e5 + 5;
int n, m, h[N], dis[N];
vector<pi> e[N];

inline int read() {
    int x;
    cin >> x;
    return x;
}

signed main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    n = read(), m = read();
    for (int i = 1; i <= m; i++) {
        int u = read(), v = read(), w = read();
        e[u].push_back(make_pair(v, w));
    }
    for (int i = 1; i <= n; i++) {
        bool found = false;
        for (int j = 1; j <= n; j++)
            for (auto it : e[j])
                if (h[j] + it.second < h[it.first])
                    found = 1, h[it.first] = h[j] + it.second;
        if (i == n && found) puts("-1"), exit(0);
    }
    priority_queue<pi, vector<pi>, greater<pi>> q;
    for (int i = 1; i <= n; i++) {
        int ans = 0;
        for (int j = 1; j <= n; j++)
        	dis[j] = (i == j ? 0 : 1e9);
        q.push(make_pair(0, i));
        while (q.size()) {
            auto t = q.top();
            q.pop();
            int id = t.second;
            if (t.first != dis[id]) continue;
            for (auto v : e[id]) {
                int it = v.first, d = t.first + h[id] - h[it] + v.second;
                if (d < dis[it]) q.push({dis[it] = d, it});
            }
        }
        for (int j = 1; j <= n; j++)
            ans += j * (dis[j] + (dis[j] < 1e9 ? h[j] - h[i] : 0));
        cout << ans << endl;
    }
    return 0;
}

1.4.2 Floyd 与传递闭包

Floyd 也可以解决带负权边的图的全源最短路径问题。

设 \(dis_{k, s, t}\) 表示 \(s\rightsquigarrow t\) 只经过编号不大于 \(k\) 的点（两端除外）的最短路。从 \(f_k\) 推到 \(f_{k + 1}\) 时，只需考虑往两点之间的最短路当中插入 \(k + 1\)，即枚举 \(i, j\)，用 \(dis_{k, i, k + 1} + dis_{k, k + 1, j}\) 更新 \(dis_{k + 1, i, j}\)。

省去第一维导致的重复更新不影响答案，因为最短路不经过重复点。简化后的算法描述为：初始化所有 \(dis_{u, u} = 0\)，以及 \((u\to v) \in E\) 的 \(dis_{u, v}\) 为 \(w_{u, v}\)，其它为无穷大。枚举中转点 \(k\)，起点 \(i\)，终点 \(j\)，用 \(dis_{i, k} + dis_{k, j}\) 更新 \(dis_{i, j}\)。注意 中转点必须在最外层枚举。

很明显，按任意顺序枚举中转点，甚至枚举相同的中转点，只要每个点至少一次作为中转点，依然能得到正确的答案。

算法的时间复杂度为 \(\mathcal{O}(n ^ 3)\)。不仅好写，而且在稠密图上运行效率高于 Johnson，因此 Floyd 是数据规模较小时最短路算法的最佳选择。

此外，Floyd 可以求传递闭包。有向图 \(G\) 的 传递闭包 定义为 \(n\) 阶布尔矩阵 \(T\)，满足 \(T_{i, j} = 1\) 当且仅当 \(i\) 可达 \(j\)，否则为 \(0\)。有边的点对之间初始化 \(T_{u, v} = 1\)，转移时内层操作为 \(T_{i, j} \gets T_{i, j} \lor (T_{i, k} \land T_{k, j})\)，其中 \(\lor\) 表示逻辑或，\(\land\) 表示逻辑与。

• bitset 优化求传递闭包的复杂度至 \(\mathcal{O}(\frac {n ^ 3} w)\)。
• 对于稀疏有向图，缩点后拓扑排序可做到 \(\mathcal{O}(\frac {nm} w)\) 求传递闭包。

1.5 扩展问题

默认图（弱）连通且无负环。

1.5.1 最短路树

从 \(s\) 开始求图上每个点的单源最短路径。对于 \(i\neq s\)，\(i\) 的最短路由点 \(j\) 扩展而来，满足 \(dis_j + w(j, i) = dis_i\)，即 \(s\rightsquigarrow i\) 的最短路是 \(s\rightsquigarrow j\) 的最短路加入边 \((j, i)\) 得到。我们希望用一个结构刻画 \(s\) 到每个点的最短路。

在单源最短路径过程中，记录每个点最后一次被更新最短路的对应前驱 \(f_i\)。即若当前松弛边 \((j, i)\) 且 \(dis_j + w(j, i) < dis_i\)，则令 \(f_i\gets j\)。除了源点 \(s\)，从 \(f_i\) 向 \(i\) 连边，则形成的有向图无环。

这样，得到一棵有根叶向树，称为 从 \(s\) 出发的最短路树，每个点的 \(f_i\) 为其父亲。最短路树上从 \(s\) 出发到 \(i\) 的简单路径就是原图 \(s\rightsquigarrow i\) 的最短路。

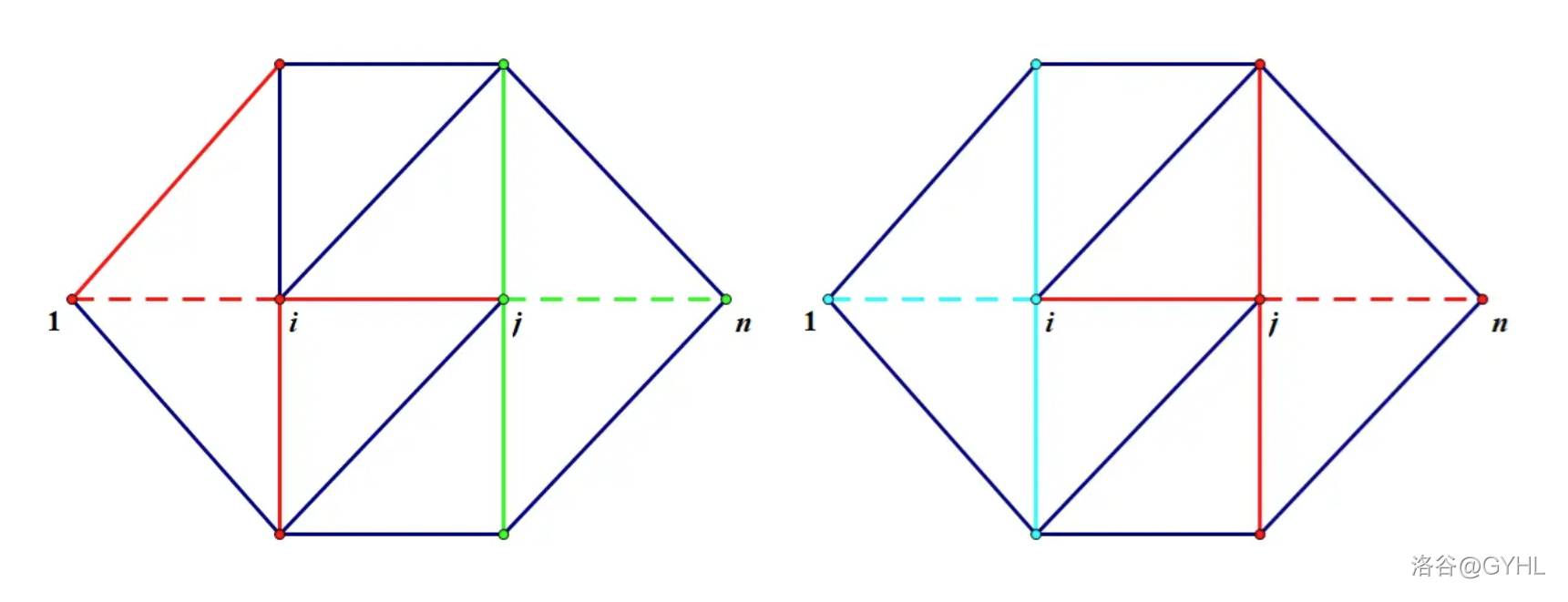
一张图的最短路树不唯一，如下图所示（无向图）。

最短路树以外的所有边不影响 \(s\) 到各个点的最短路，可以忽略。

类似地，将图上所有边翻转方向后求得的以 \(s\) 为根的最短路树，就是原图 到达 \(s\) 的最短路树，它是一棵根向树。无向图不区分边的方向，所以从 \(s\) 出发的最短路树也可以是到达 \(s\) 的最短路树，但有向图并不一定。

最短路树在求解单源最短路径问题的变形时发挥了很大的作用，如接下来介绍的删边最短路。

扩展：在 不含零环的图上 将 \(dis_j + w(j, i) = dis_i\) 的 \(j\to i\) 加入结构，得到一张有向无环图，称为 最短路 DAG。最短路计数相当于 DAG 路径计数，拓扑排序后 DP。最短路 DAG 的任意一棵生成树均为最短路树。最短路树计数相当于 DAG 生成树计数，使用矩阵树定理求解。

例题：P6880。

1.5.2 删边最短路

问题描述：给定一张 无向正权图，对图上的每条边，求删去该边后 \(1\rightsquigarrow n\) 的最短路。

首先求出 \(1\rightsquigarrow n\) 的最短路 \(P = p_0(1)\xrightarrow {e_1} p_1 \xrightarrow {e_2} \cdots \xrightarrow {e_L} p_L(n)\)。设 \(e\) 表示当前考虑的边 \((i, j)\)。

若 \(e\notin P\)，答案是显然的：删去一条边后最短路不可能变短，故 \(1\rightsquigarrow n\) 的最短路仍为 \(w(P)\)。

若 \(e\in P\)，考虑求出 从 \(1\) 出发 和 到达 \(n\) 的最短路树 \(T_1\) 和 \(T_n\)，要求 \(T_1\) 上 \(1\rightsquigarrow n\) 的路径等于 \(T_n\) 上 \(1\rightsquigarrow n\) 的路径等于 \(P\)。枚举每一条边 \((u, v)\)（注意一条边可以从两个方向经过）。若 \(T_1(1\rightsquigarrow u)\) 和 \(T_n(v\rightsquigarrow n)\) 均不包含 \((i, j)\)，那么用 \(w(T_1(1\rightsquigarrow u)) + w(u\to v) + w(T_n(v\rightsquigarrow n))\) 更新最短路。这个做法本质上是 存在最短路只走一条 “非树边”，指：这条非树边之前的路径全部在 \(T_1\) 上，之后的路径全部在 \(T_n\) 上。

证明

不妨设 \(i, j\) 在 \(P\) 上的顺序为 \(i\to j\)。

设 \(A_j\) 和 \(A_i\) 分别表示 \(T_1\) 上 \(j\) 的子树和 \(j\) 的子树以外的部分。设 \(B_i\) 和 \(B_j\) 分别表示 \(T_n\) 上 \(i\) 的子树和 \(i\) 的子树以外的部分。

引理

\(A_j\cap B_i = \varnothing\)。

如上图，绿色部分的 \(A_j\) 和蓝色部分的 \(B_i\) 无交。

证明

假设存在 \(u\in A_j \cap B_i\)。因为 \(e\in P\subseteq T_1\)，所以 \(1\rightsquigarrow u\) 的最短路形如 \(1\rightsquigarrow i\to j\rightsquigarrow u\)（在 \(T_1\) 上）。因为 \(e\in P\subseteq T_n\)，所以 \(u\rightsquigarrow n\) 的最短路形如 \(u\rightsquigarrow i\to j\rightsquigarrow n\)（在 \(T_n\) 上）。

根据最短路的性质，有 \(w(T_1(i\to j\rightsquigarrow u))\leq w(T_n(i\rightsquigarrow u))\) 以及 \(w(T_n(u\rightsquigarrow i\to j)) \leq w(T_1(u\rightsquigarrow j))\)。注意这里将最短路树上的路径进行了翻转，这用到了 原图为无向图 的性质（\(w(T_n(u\rightsquigarrow i)) = w(T_n(i\rightsquigarrow u))\)）。对于有向图，不等式右侧不一定存在。

将左侧路径拆开，右侧路径翻转，得 \(w(i\to j) + w(T_1(j\rightsquigarrow u)) \leq w(T_n(u\rightsquigarrow i))\) 以及 \(w(T_n(u\rightsquigarrow i)) + w(i\to j) \leq w(T_1(j\rightsquigarrow u))\)。

两式相加，得 \(2w(i\to j) \leq 0\)，与正权图矛盾。\(\square\)

简单地说，根据 \(u\in A_j\cap B_i\) 可以推出 \(a + c \leq b\) 和 \(a + b\leq c\)，得 \(2a\leq 0\)。如上图。

考虑删去 \(e = (i, j)\) 后任意一条 \(1\to n\) 的最短路 \(P'\)。因为 \(1\in A_i\)，\(n\in A_j\)，所以存在 \(e' = (u, v)\in P'\) 使得 \(u\in A_i\)，\(v\in A_j\)。不妨设 \(e'\) 是路径上最后一条这样的边。

将 \(P'\) 上 \(1\rightsquigarrow u\) 的部分替换成 \(T_1(1\rightsquigarrow u)\) 一定不劣，因为后者是 \(1\rightsquigarrow u\) 的最短路。又因为 \(u\in A_i\)，所以这部分一定不会包含 \(i\to j\)。

将 \(P'\) 上 \(v\rightsquigarrow n\) 的部分替换成 \(T_n(v\rightsquigarrow n)\) 一定不劣，因为后者是 \(v\rightsquigarrow n\) 的最短路。又因为 \(v\in A_j\)，根据引理，\(v\notin B_i\)，即 \(v\in B_j\)，所以这部分同样不会包含 \(i\to j\)。

这样，对于删去 \(e\) 后的任意最短路，总存在调整它的方案使得恰好只经过 \(e'\) 一条非树边。而枚举每条非树边计算最短路长度并更新的过程考虑到了所有恰好只经过一条非树边的路径，相对应的也就考虑到了所有最短路。算法正确性得证。

尽管如此，对一条边求答案仍需要 \(\mathcal{O}(m)\) 的时间。

枚举 \(e = (u, v)\)，求出 \(T_1\) 上 \(n\) 和 \(u\) 的 LCA，即最短路 \(1\rightsquigarrow n\) 和 \(1\rightsquigarrow u\) 的最后一个公共交点，设为 \(u'\)。类似地，设 \(v' = T_n(lca(v, 1))\)。则 \(w(T_1(1\rightsquigarrow u)) + w(u\to v) + w(T_n(v\rightsquigarrow n))\) 可以用于更新 \(P\) 上 \(u'\rightsquigarrow v'\) 之间所有边的答案。正确性留给读者思考。

线段树维护区间取 \(\min\) 或 multiset 离线扫描线，时间复杂度 \(\mathcal{O}(m\log m)\)。

扩展：一开始我们要求 \(P\in T_1\cap T_n\)，实际上这是不必要的。根据 \(T_1\) 求出 \(P\) 之后，可以将 \(v'\) 的定义改为 \(T_n(v\rightsquigarrow n)\) 和 \(P\) 的第一个交点而不影响答案，因为将 \(P(v'\rightsquigarrow n)\) 接在 \(T_n(v\rightsquigarrow v')\) 之后一定不劣，相当于手动钦定了 \(P\in T_1\cap T_n\)。

扩展：对于存在零权边的非负权图，导出矛盾的 \(2w(i\to j)\leq 0\) 失效了。做出修正：求出 \(u'\) 后，若 \(u'\) 的父边权值为 \(0\)，则不断向上跳父亲。对于 \(v'\) 同理。这样我们的调整法又可以用了，具体证明就略去了。也可以将边权为 \(0\) 的边两侧缩成一个点，不过这样处理起来麻烦一点。

例题：P1186，P2685，P3573，CF1163F。有向图删边最短路 P3238 是假题，不可做。

1.5.3 平面图最小割

前置知识：割的定义。

• 平面图：能画在平面上，满足除顶点处以外无边相交的图称为 平面图。
• 网格图：形成一个网格的平面图称为 网格图。形式化地，对于点数为 \(n\times m\) 的网格图，存在一种为每个点赋互不相同的标号 \((i, j)\)（\(1\leq i\leq n\)，\(1\leq j\leq m\)）的方案，满足两点之间有边当且仅当它们的 \(j\) 相同且 \(i\) 相差 \(1\)，或 \(i\) 相同且 \(j\) 相差 \(1\)。

一般平面图最小割问题都在网格图上，所以我们先介绍网格图最小割，满足 边权非负 且 割的源点和汇点在边界 上。称一个点在边界上，当且仅当它的 \(i\) 等于 \(1\) 或 \(n\)，或 \(j\) 等于 \(1\) 或 \(m\)。

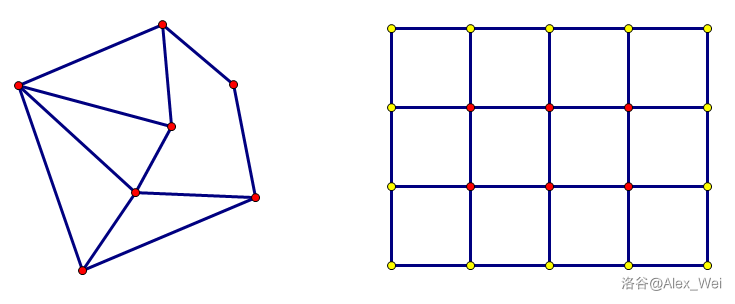
如上图，左边是一张平面图，右边是一张网格图，边界上所有点用黄色标注。

考虑求网格图左上角 \(s\) 到右下角 \(t\) 的最小割，即一种划分点集的方式 \(V = S\sqcup T\)（\(\sqcup\) 表示无交并，即 \(S\cup T = V\)，\(S\cap T = \varnothing\)），满足 \(s\in S\)，\(t\in T\) 且两端分别在 \(S, T\) 的边（称为割边）的权值之和（称为割的权值）最小。

引理

总存在权值最小的割满足 \(S\) 的所有点连通，\(T\) 的所有点连通。

证明

假设 \(S\) 的点不连通，那么存在不包含 \(s\) 的连通块 \(S'\)。将 \(S'\) 并入 \(T\)，原来的非割边不会变成割边，而一些割边变成非割边，所以割的权值不会变大。\(\square\)

考虑 \(S\) 和 \(T\) 的边界。这个边界对应了一条从右上到左下的路径。在两个相邻的面之间移动时，需要花费对应边权的代价，那么路径长度就对应了割的权值。如下图。

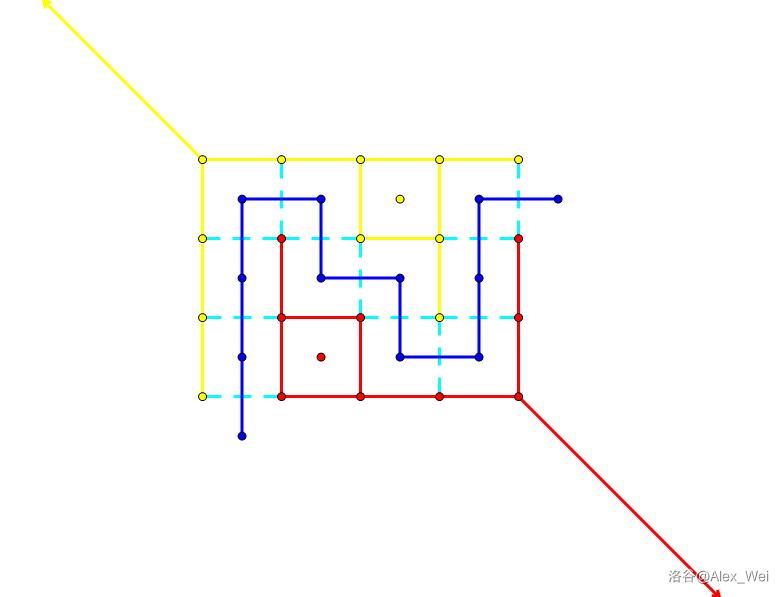
考虑从左上角和右下角向外引出两条权值无穷大的射线，将网格图外的平面分成左下和右上两部分。现在我们要建出网格图的 对偶图：将所有面抽象成点，对于通过一条边相邻的两个面，在它们对应的点之间连权值为这条边的权值的边（这不是对偶图的严谨定义）。

一个满足 \(S\) 连通，\(T\) 连通的割，恰对应了对偶图上从右上无穷面代表的点到左下无穷面代表的点的路径，因此 网格图最小割等于对偶图最短路，如下图。

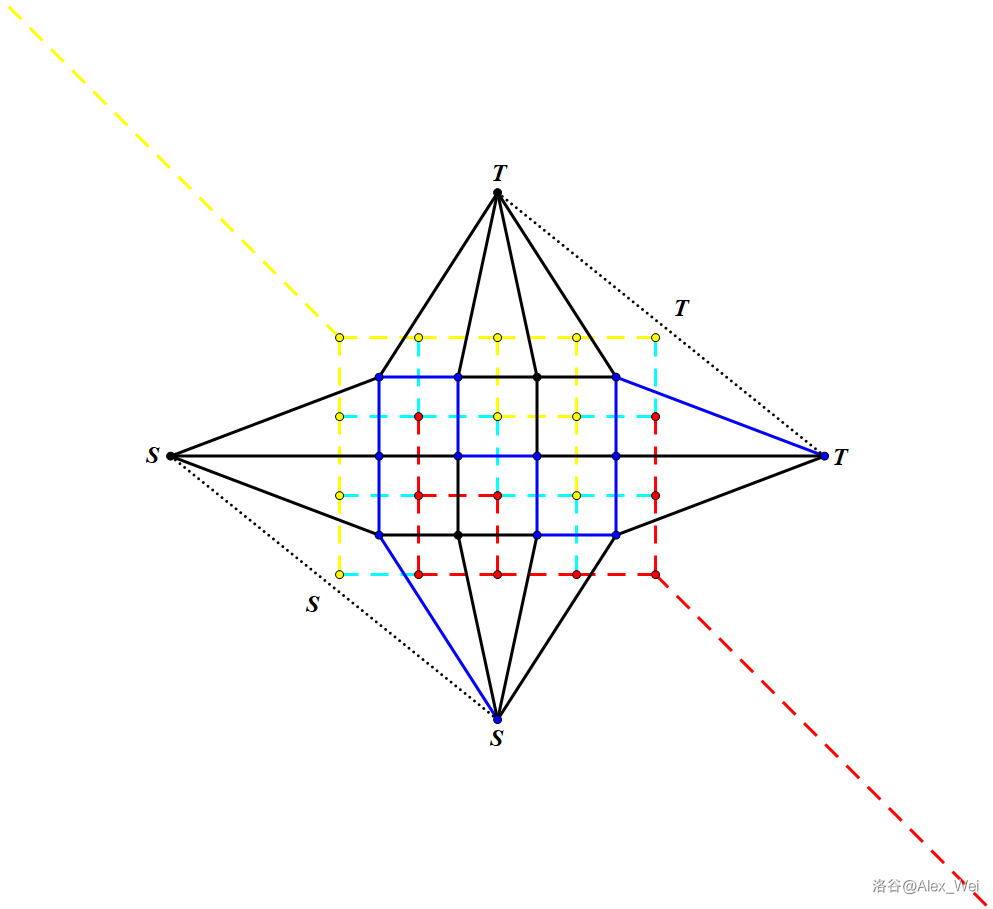
实边表示对偶图的边，虚边表示原图的边。注意左侧和下侧，上侧和右侧分别是同一个点。从右上到左下的最短路即为左上到右下的最小割。上图给出了一条可能的最短路以及它对应的最小割。

扩展：不需要源汇在左上角和右下角。只要源汇在边界上，就可以通过转对偶图的方式求最小割。

扩展：不需要是网格图。平面图也可以转对偶图求最小割，整个过程没有用到网格图的性质，只是便于理解。

例题：P4001，P7916。

*1.5.4 \(k\) 短路

前置知识：可持久化线段树或其它可持久化结构。

问题描述：给定一张 有向非负权 图，求 \(s\rightsquigarrow t\) 的前 \(k\) 短路径长度。对于无向图，将无向边拆成两条有向边即可。

\(k\) 短路严格强于最短路，所以无论如何都需要跑一次最短路算法。

一个解决问题的有效思路是：找一种好的方式刻画研究对象，这里 “好的” 指便于考虑和解题。\(k\) 短路问题的研究对象是 \(s\rightsquigarrow t\) 的路径，所以我们希望找到一种好的刻画路径的方式。我们知道刻画最短路的方式是最短路树，而 \(k\) 短路在一定程度上也是最短路问题，所以：在反图上跑最短路，建出到达 \(t\) 的最短路树 \(T\)（建从 \(s\) 出发的最短路树也可以做），有多棵选任意一棵。

考虑一条 \(s\rightsquigarrow t\) 的路径的形态。因为一条边要么是树边，要么是非树边，所以路径上会有一些非树边和树边形成的连续段。每个树边连续段对应一条 \(T\) 上的路径，满足连续段结束的端点在起始端点到 \(t\) 的路径上。

进一步地，发现一个 有序 的非树边序列 \(P = [e_1, e_2, \cdots, e_p]\) 可以 唯一确定 一条 \(s\rightsquigarrow t\) 的路径。其中，根据上述分析，需要满足对于任意相邻非树边 \(e_i, e_{i + 1}\)，\(u(e_{i + 1})\) 在 \(T\) 上是 \(v(e_i)\) 的祖先，此外 \(u(e_1)\) 是 \(s\) 的祖先。如下图。容易证明 \(P\) 和路径的一一对应关系。

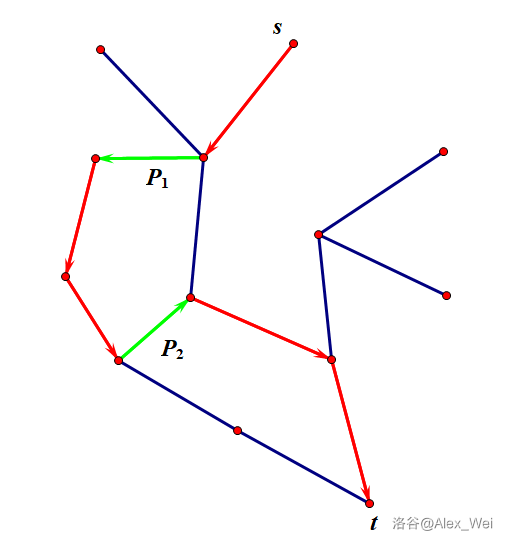
这很优秀，因为直觉告诉我们 \(k\) 短路相较于最短路相差不会太大，而导致它们差异的地方就在于经过了一些不太优的非树边，我们精确刻画了这些非树边的形态，且和原路径一一对应了。那么一个思想是不断添加非树边，通过调整法得到次短路，第三短路，以此类推。

还有一个问题：在研究 \(P\) 的过程中，我们丢掉了树边的权值。这对路径长度的统计是致命的。解决方法：当序列末尾加入非树边 \(e = (u, v, w)\) 时，本来从 \(u\) 沿最短路走到 \(t\) 变成先经过 \(e\)，再从 \(v\) 沿最短路走到 \(t\)，有 \(\delta(e) = (dis_v + w) - dis_u\)，其中 \(dis_i\) 表示 \(i\rightsquigarrow t\) 的最短路长度。进一步地，可以证明 \(P\) 对应路径的长度等于 \(s\rightsquigarrow t\) 的最短路加上所有非树边的 \(\delta\) 之和，即：

\[dis_s + \sum_{e\in P} \delta(e)
\]

注意到 \(dis_s\) 是定值，这样路径长度也只和 \(P\) 有关了。问题转化为求权值前 \(k\) 小的合法的 \(P\)。

这类 “不断扩展结构，取出权值前 \(k\) 小” 的问题非常经典，解法如下：对每个除了权值最小的结构，为其钦定一个权值不比它大的前驱，满足前驱关系不成环。这样，任何结构都可以从唯一的无前驱的权值最小的前驱开始扩展得到，满足每次扩展一个前驱为当前结构的结构，即每次扩展一个后继。用优先队列维护所有被扩展但未被考虑的结构，第 \(i\) 次取出队列中权值最小的结构就是权值第 \(i\) 小的结构，然后将其所有后继加入优先队列。

证明

假设第 \(i\) 次取出队列的结构 \(Z\) 不是权值第 \(i\) 小的结构，且 \(i\) 是所有这样的操作中编号最小的。考虑第 \(i\) 小的结构 \(Y\)，其前驱 \(X\) 一定被考虑过：\(X\) 的排名小于 \(i\)，而根据假设，前 \(i - 1\) 次操作均取出了正确的结构，所以 \(X\) 被正确取出了。所以 \(Y\) 一定在优先队列中且 \(Y\) 小于 \(Z\)。这和当前取出 \(Z\) 矛盾了。\(\square\)

只要每个点的后继数量不大，那么时间复杂度为 \(\mathcal{O}(k(a\log k + b))\)，其中 \(a\) 表示每个点的后继数量，\(b\) 表示查询所有后继的复杂度。

回归原问题，一个设置前驱的方案为：令 \(P\) 的前驱为删去 \(e_{p}\) 得到的序列，但这将导致一个序列有 \(\mathcal{O}(m)\) 个后继：从 \(v(e_{p})\) 在 \(T\) 上任意祖先出发的所有边均可加入 \(P\)。

解决方法也是经典的：前驱不一定要减少元素个数，也可以减小最后一个元素的权值。对此，加入限制：设 \(v(e_{p - 1})\) 在 \(T\) 上的祖先集合为 \(A\)，若 \(e_{p}\) 不是从 \(A\) 出发的 \(\delta\) 最小的边，那么删去 \(e_{p}\)，加入它的从 \(A\) 出发的 \(\delta\) 前驱，否则删去 \(e_{p}\)。即设从 \(A\) 出发的所有边按 \(\delta\) 从小到大排序后分别为 \(c_1, c_2, \cdots, c_d\)，将 \(e_{p}\) 替换为它在该序列的前驱。若前驱不存在则直接删去 \(e_{p}\)。

这样，一个序列至多有两个后继：

• 如果 \(e_{p}\) 不是从 \(A\) 出发的 \(\delta\) 最大的边，那么将其删去，改成后继。
• 加入从 \(v(e_{p})\) 在 \(T\) 上任意祖先出发的 \(\delta\) 最小的边。

容易证明这是我们钦定的前驱关系对应的后继关系。用可持久化权值线段树维护最短路树上从一个点的所有祖先出发的所有边，查后继和权值最小的边均可线段树二分。

综上，时间和空间复杂度是关于 \(n, m, k\) 的线性对数。具体分析可知时间为 \(\mathcal{O}((m + k)\log m + k\log k)\)，空间为 \(\mathcal{O}(m\log m + k)\)。

注意 \(|P| = 0\) 或 \(1\) 时需要特殊讨论，此时 \(e_{p - 1}\) 和 \(e_p\) 可能不存在。不要忘记 \(u(e_1)\) 需要是 \(s\) 的祖先。

扩展：存在负权边会使得一开始求最短路的复杂度变成 \(\mathcal{O}(nm)\)，而求 \(k\) 短路的复杂度不受影响。

扩展：对于 \(k\) 短路，使用可持久化可并堆可以做到更优秀的复杂度。见参考资料。

例题：P2483。

1.5.5 同余最短路

同余最短路算法可以求出在给定范围内有多少重量可由若干物品做完全背包得到，即一段区间内有多少数可由给定正整数进行 系数非负 的线性组合得到。

问题描述：给定 \(n\) 个正整数 \(a_i\)，求有多少个整数 \(y\in [L, R]\) 可以表示为 \(\sum_{c_i} a_ic_i\)，其中 \(a_i\) 较小，\(c_i\) 是非负整数，\(L, R\) 较大。

其核心在于观察到，如果一个数 \(r\) 可以被表出，那么任何 \(r + xa_i\)（\(x \geq 0\)，\(1\leq i\leq n\)）也可以被表出。选出一个 \(a_i\)，求出每个模 \(a_i\) 同余的同余类 \(K_j\) 当中最小的能被表出的数 \(f_j\)，即可快速判断 \(y\) 能否被表出：当且仅当 \(y \geq f_{y\bmod a_i}\)。

一种理解方式：考虑每个数能否被表出，设为 \(g(r)\)。对于某个 \(a_i\)，如果 \(r_1\equiv r_2\pmod {a_i}\) 且 \(r_1 < r_2\)，那么 \(g(r_1) \leq g(r_2)\)。这样，根据定义域值域互换的技巧，设 \(f_j\) 表示使得 \(g(r) = 1\) 且 \(r\bmod {a_i} = j\) 的最小的 \(r\)。

为减小常数，一般选择使得同余类个数最少的 \(a_i\)，即 \(a\) 的最小值，设为 \(a_1\)。得到模 \(a_1\) 余 \(j\) 的数中最小的能被表出的数 \(f_j\) 后，加上 \(a_2 \sim a_n\) 转移到其它同余类 \(f_{(j + a_i) \bmod a_1}\)。

上述过程非常像一个最短路：对于每个点 \(j\)，它向 \((j + a_i) \bmod a_1\) 连长度为 \(a_i\) 的边，求从源点 \(0\) 开始到每个点的最短路。使用 Dijkstra 或 SPFA 求解。

求出 \(f_j\) 后容易求答案。差分转化为求 \([0, R]\) 有多少个数能被表出，即

\[\sum_{i = 0} ^ {a_1 - 1} \max \left(0, \left\lfloor \frac{R - f_i} {a_1} \right\rfloor + 1\right)
\]

用 \([0, R]\) 的答案减去 \([0, L - 1]\) 的答案即可。

时间复杂度为 Dijkstra 的 \(\mathcal{O}(na_1\log a_1)\) 或 SPFA 的 \(\mathcal{O}(n a_1 ^ 2)\)。

存在 \(\mathcal{O}(na_1)\) 的做法，见 同余最短路的转圈技巧（含例题 P2371，P9140）。

例题：ARC084B，P4156（见 “字符串进阶 I”）。

1.6 例题

P1462 通往奥格瑞玛的道路

最小化最大值，考虑二分答案并使用 Dijkstra 检查 \(1\to n\) 的最短路是否不大于 \(b\)。

时间复杂度 \(\mathcal{O}(n\log n \log c)\)。代码。

P4568 [JLOI2011] 飞行路线

注意到 \(k\) 很小，跑最短路时记录当前用了几条免费边即可。相当于在分层图（将原图复制若干次）上跑最短路。

时间复杂度 \(\mathcal{O}(mk\log(mk))\)。代码。

P6880 [JOI 2020 Final] 奥运公交

不翻转的情况是平凡的。考虑翻转，将贡献拆为 \(1\rightsquigarrow n\) 和 \(n\rightsquigarrow 1\)。

对于 \(1\rightsquigarrow n\)，建出 \(1\) 开始的最短路树。

• 若边 \(i\) 不在最短路树上，因为最短路要么经过 \(e_i\)，要么不经过。对于前者，即 \(1\rightsquigarrow v_i\) 的最短路，加上 \(w_i\)，再加上 \(u_i\rightsquigarrow n\) 的最短路。对于后者，最短路即原最短路。两种情况都可以预处理后 \(\mathcal{O}(1)\) 计算。
• 如果边 \(i\) 在最短路树上，可以重新跑最短路，因为总共只有 \(\mathcal{O}(n)\) 条最短路树上的边。稠密图，用 \(\mathcal{O}(n ^ 2)\) Dijkstra 跑最短路。

对于 \(n\rightsquigarrow 1\)，同理。

时间复杂度 \(\mathcal{O}(n(n ^ 2 + m))\)。做到 \(\mathcal{O}(m + n ^ 3)\) 需要一些细节处理。代码。

P4001 [ICPC-Beijing 2006] 狼抓兔子

网格图最小割。建出网格图的对偶图，每条边与其对偶边权值相等。从右上到左下的最短路即为所求。

代码。

CF1765I Infinite Chess

直接 BFS，复杂度高达 \(8\times 10 ^ 8\)，无法接受。

注意到行数很少，这样斜向攻击只会影响到半径为 \(8\) 的列邻域。而对于横向攻击，我们可以把一段每行被攻击状态相同的列缩成一列，相当于离散化。注意国王可以斜向走，所以两侧还要保留 \(8\) 列。

离散化后模拟得到每个格子是否被攻击，跑最短路即可。时间复杂度 \(\mathcal{O}(n\log n)\)。代码。

P4926 [1007] 倍杀测量者

化乘法为加法不难想到取对数。

考虑对没有女装的限制建出差分约束图，若出现负环则一定有人女装。对于固定分数的人 \(i\)，让 \(0, i\) 之间互相连边权分别为 \(\log x_i\) 和 \(-\log x_i\) 的边即可。

答案显然满足可二分性。

时间复杂度 \(\mathcal{O}(ns\log V)\)。代码。

*P5304 [GXOI/GZOI2019] 旅行者

\(\mathcal{O}(m\log m \log k)\) 做法的核心思想是 二进制分组 后跑最短路。两个不同的数的二进制必定至少有一位不同，所以每两个关键点之间的最短路均被统计到。代码。

随机分组也可以，做 \(k\) 次的正确性是 \(1 - \left(\dfrac 3 4 \right) ^ k\)。类似题目如 CF1314D。

\(\mathcal{O}(m\log m)\) 做法的思想很巧妙。预处理每个特殊城市到点 \(i\) 的最短距离 \(f_i\) 和对应城市 \(fr_i\)，以及点 \(i\) 到所有特殊城市的最短距离 \(g_i\) 和对应城市 \(to_i\)。对于每条边 \(u\to v\)，若 \(fr_u \neq to_v\)，则用 \(f_u + w_{u, v} + g_v\) 更新答案。

考虑任意最优路径 \(i\rightsquigarrow j\)，因为 \(fr_i = i\) 且 \(to_j = j\)，所以路径上必然至少有一条边 \(u\to v\) 满足 \(fr_u\neq to_v\)，\(fr_u\neq j\) 且 \(to_v\neq i\)，反证法易证。那么 \(f_u\) 一定等于 \(i\rightsquigarrow u\) 的最短路，\(g_v\) 一定等于 \(v\rightsquigarrow j\) 的最短路，否则将 \(i\) 替换为 \(fr_u\) 或 \(j\) 替换为 \(to_v\) 一定更优。

代码。

*P5590 赛车游戏

好题。

转换思路，与其设置边权使路径长度相等，不如设置路径长度去拟合边权的限制。

设 \(d_i\) 为 \(1\to i\) 的最短路，只需保证对于所有边 \((u,v)\) 有 \(w_{u,v}=d_v-d_u\) 即可使任意一条简单路径长相等。于是 \(1\leq d_v-d_u\leq 9\)，转化为 \(d_u+9\geq d_v\) 与 \(d_v-1\geq d_u\)，差分约束求解即可。注意不在 \(1\to n\) 的任意一条路径上的边没有用，这些边不应计入限制，随便标权值。

时间复杂度 \(\mathcal{O}(nm)\)。代码。

*ABC232G Modulo Shortest Path

将所有点按照 \(b\) 值从小到大排序。对于一个点连出去的所有边，连向一段前缀的点的权值形如 \(a_i + b_j\)，连向一段后缀的点的权值形如 \(a_i + b_j - m\)，容易找到分界点。

考虑朴素 Dijkstra 的过程，发现操作本质上是：区间 \(c_i\) 对 \(v\) 取 \(\min\)，单点修改 \(d_i\)，全局查询 \(\min c_i + d_i\) 以及对应位置。线段树区间维护 \(d_i\) 和 \(c_i + d_i\) 的最小值及其位置即可。

时间复杂度 \(\mathcal{O}(n\log n)\)。代码。

本题的官方解法非常精妙：取模操作可以想象成在环上走。考虑建立虚点 \(x_{0\sim m - 1}\)，从 \(x_i\to x_{(i + 1)\bmod m}\) 连权值为 \(1\) 的边，让它们连成一个环。从 \(i\) 向 \(x_{-a_i\bmod m}\)，从 \(x_{b_i\bmod m}\) 向 \(i\) 连权值为 \(0\) 的边，可准确表示出所有边。环上点数为 \(\mathcal{O}(m)\)，但可以将环上的若干段点缩起来，做到点数 \(\mathcal{O}(n)\)。跑 Dijkstra 即可，时间复杂度 \(\mathcal{O}(n\log n)\)。

P3573 [POI2014] RAJ-Rally

本题可以借助删边最短路的思想，枚举除了最长链以外的所有点，用线段树维护它对最长链上一段区间的贡献。因为保证有向图无环，所以可行。需要添加虚点保证弱连通。

另外一种思路：删去点 \(u\) 后有三种路径：拓扑序全部比 \(u\) 小，拓扑序全部比 \(u\) 大，或拓扑序跨过 \(u\)。前两种好处理，对于第三种，在跨过拓扑序的边上统计答案。按拓扑序扫描，每次加入从拓扑序前驱出发的边的贡献，删去到达当前点的边的贡献，用 multiset 维护。

时间复杂度 \(\mathcal{O}(m\log m)\)。代码。

*P3530 [POI2012] FES-Festival

一道加深对差分约束理解的好题。

首先建出差分约束图。跑一遍负环判无解。

但如何满足不同的 \(t\) 值数量最大呢？差分约束无法解决这样的问题。

首先强连通分量缩点（见第四章强连通分量），不同 SCC 之间独立，因为可以将两个 SCC 之间的距离任意拉远。

考虑 SCC 内部的贡献。不妨设 \(t_u\) 取到了下界，\(t_v\) 取到了上界，根据差分约束的实际意义，需要满足 \(t_u + d_{u, v}\geq t_v\)，其中 \(d_{u, v}\) 表示 \(u\rightsquigarrow v\) 的最短路。令 \(t_v = t_u + d_{u, v}\)，那么 \(t_u\sim t_v\) 是否都能取到呢？因为正权边权值均为 \(1\)，所以最短路路径上所有点必然取遍了 \(t_u\sim t_v\) 这 \(d_{u, v} + 1\) 个值。

考虑最短路的最大长度 \(d_{u, v}\)。首先容易证明 SCC 内部的答案可以取到 \(d_{u, v} + 1\)：根据三角形不等式，令 \(t_i = t_u + d_{u, i}\) 一定合法，且上文说明了 \(t_u\sim t_u + d_{u, v}\) 所有取值均出现过。若答案更大，设 \(t_u'\) 取到下界，\(t_v'\) 取到上界，则 \(d_{u', v'}\) 无论如何都得大于 \(d_{u, v}\)，与 \(d_{u, v}\) 最大矛盾。因此答案为 \(\max d_{u, v} + 1\)。

因为图是稠密图，所以使用 Floyd 求解任意两点之间的最短路。答案即每个 SCC 的答案之和。

时间复杂度 \(\mathcal{O}(n ^ 3)\)。代码。

*P7916 [CSP-S 2021] 交通规划

\(k = 2\) 是经典 “狼抓兔子”，平面图最小割转对偶图最短路。

\(k > 2\) 类似。平面图转对偶图后，最外层会出现 \(k\) 个结点。对于一个点 \(i\)，设其逆时针方向的射线颜色和顺时针方向的射线颜色分别为 \(L_i\) 和 \(R_i\)，取值为 \(0\) 或 \(1\)，表示白或黑。若 \(L_i = R_i\)，那么 \(i\) 相邻的两个射线处于同一连通块是最优的。因为任何将它们分割开的方案，通过调整使得它们在同一连通块后代价总会减少。

显然，\((L_i, R_i)\) 等于 \((0, 1)\) 和 \((1, 0)\) 的结点个数相同。每个 \((0, 1)\) 和 \((1, 0)\) 匹配，路径经过的所有边两端颜色不同。因此这样的匹配方案总能给出一个划分方案及其代价。

关键性质是任意两点的匹配不会相交，即不会出现 \(a < b < c < d\) 且 \(a\) 匹配 \(c\)，\(b\) 匹配 \(d\)。若相交，则调整法可证不交时不劣。

因此，首先求出所有 \((0, 1)\) 和 \((1, 0)\) 点之间两两最短路。求匹配最小代价可以类似括号匹配，破环成链后区间 DP。

时间复杂度 \(\mathcal{O}(knm\log(nm) + k ^ 3)\)。细节较多，代码。

*ARC084B Small Multiple

好题。

所有正整数都可以从 \(1\) 开始经过若干次 \(+1\) 和 \(\times 10\) 得到。从 \(i\) 向 \((i + 1) \bmod K\) 连权值为 \(1\) 的边，向 \(10i \bmod K\) 连权值为 \(0\) 的边，求 \(1\to 0\) 的最短路即可。

注意不可以将 \(0\) 作为源点，因为题目要求正整数倍。

时间复杂度 \(\mathcal{O}(K)\)。代码。

*AGC056C 01 Balanced

将 \(0\) 看成 \(1\)，\(1\) 看成 \(-1\)，问题限制是差分约束的形式。

对于限制 \(L - 1, R\)，互相连长度为 \(0\) 的边。

对于相邻的两个位置 \(i - 1\) 和 \(i\)，要求 \(|v_i - v_{i - 1}| = 1\)。看似没有办法描述，不过当限制变为 \(|v_i - v_{i - 1}|\leq 1\) 时，可以在 \(i\) 和 \(i - 1\) 之间互相连长度为 \(1\) 的边，并最大化 \(v\) 的字典序。回忆差分约束本身自带字典序极值性质。

我们惊讶地发现，在保证字典序最大的前提下，不可能出现 \(v_i = v_{i + 1}\) 的情况。模拟最短路的过程，可以证明 \(v_i\) 的奇偶性是固定的，并且相邻两个 \(v\) 的奇偶性一定不同：\(0\) 边连接的两个点的下标奇偶性相同（题目保证了这一点），\(1\) 边则奇偶性不同。

这题的思想很高妙，虽然解法是差分约束但是形式新颖，需要猜性质（不要被固有思维限制）才能做出本题。

边权只有 \(0/1\)，01 BFS 的时间复杂度为 \(\mathcal{O}(n + m)\)。代码。

若为了避免出现 \(|v_i - v_{i - 1}| = 1\) 的限制而直接求前缀和，我们会建出带有负权边的差分约束网络。用 SPFA 求解会 TLE。

*P7516 [省选联考 2021 A/B 卷] 图函数

设一条边的边权为它的编号。

题面描述花里胡哨，我们先推些性质。

• 将 \(h\) 的值摊到每个点对 \((i, j)\) 上。
• 点对 \((i, j)(i \leq j)\) 最多只会贡献一次，因为计算 \(f(i, G)\) 时，枚举 \(v = j\) 时 \(i\) 已经被删去了，所以只可能在计算 \(f(j, G)\) 且枚举 \(v = i\) 时产生贡献。
• 模拟图函数的计算过程，点对 \((i, j)(i \leq j)\) 产生贡献当且仅当存在 \(i\to j\) 的路径 \(P\) 和 \(j\to i\) 的路径 \(Q\) 使得路径上所有点的编号不小于 \(i\)。
• 设 \(T(i, j)\) 表示所有这样的路径 \(P\) 和 \(Q\) 中，边权最小值的最大值。注意是 \(P\) 和 \(Q\) 的边权最小值而不是 \(P\) 或 \(Q\)。若 \(i = j\) 则 \(T(i, j) = m\)。则 \((i, j)\) 会对所有 \(h(G_t)(0\leq t < T(i, j))\) 产生贡献。

至此，存在 \(n ^ 3\) 的 Floyd 做法。从大到小枚举中转点 \(k\)，枚举 \(i, j\in [1, n]\)，令 \(d_{i, j}\) 和 \(\min(d_{i, k}, d_{k, j})\) 取 \(\max\)，初始值 \(d_{i, i} = m + 1\)，\(d_{i, j}(i\neq j)\) 为 \(i\to j\) 的编号，若不存在则为 \(0\)。则 \(d_{i, j}\) 表示仅考虑编号不小于 \(k\) 的节点时（不包括两端），\(i\to j\) 的边权最小值的最大值。因此，在转移 \(k\) 之前（或之后），先枚举一遍 \(j\in [k, n]\)，则 \(T(k, j) = \min(d_{k, j}, d_{j, k})\)。

这个做法严重卡常，需要加一些优化：若 \(d_{i, k} = 0\) 则不用再枚举 \(j\)，若 \(i \geq k\) 则不用再枚举。代码，可以在 LOJ 和洛谷通过。

考虑对每个 \(i\) 求出所有 \(T(i, j)(i < j)\)。将所有边按权值从大到小加入，并跳过至少一个端点编号小于 \(i\) 的边。在加入权为 \(w\) 的边时，若 \(i\rightsquigarrow j\) 且 \(j\rightsquigarrow i\)，说明 \(T(i, j) = w\)。

\(j\rightsquigarrow i\) 说明 \(i\) 在反图上可达 \(j\)。往当前图加入边 \(u\to v\) 时，若 \(u\) 可达且 \(v\) 不可达，则从 \(v\) 出发开始 bfs，将经过的点标记为可达。否则若 \(v\) 可达，则 \(u\to v\) 对连通性没有帮助，直接忽略。否则 \(u, v\) 均不可达，这条边在 \(u\) 可达时起作用，但当前没有用，所以我们保留它，将其加入 \(u\) 的邻边集合。对于反图同理，加入边 \(v\to u\)。若 \(j\) 在加入边权为 \(w\) 的边时第一次同时在原图和反图上可达，则 \(T(i, j) = w\)。每条边只会被遍历一次，时间复杂度 \(\mathcal{O}(nm)\)。代码，可以在 LOJ 和洛谷通过。

类似 ARC092F，考虑 bitset 优化。

肯定不能先枚举 \(i\) 再枚举 \((u, v)\)，这样已经 \(\mathcal{O}(nm)\) 了。考虑按权值 \(w\) 大到小添加每条边 \(u\to v\)，并 批量处理每个 \(i\)。设 \(a_{i, j}\) 表示当前 \(i\) 是否可达 \(j\)。若某个 \(i\) 需要从 \(v\) 开始 bfs，易知有 \(a_{i, u} = 1\)，\(a_{i, v} = 0\) 且 \(i\leq \min(u, v - 1)\)。因此，还要维护 \(r_{j, i}\) 表示 \(i\) 是否可达 \(j\)，则 \(r_u \land \lnot r_v\) 即可找到所有 \(i\)。

此外，维护图的邻接矩阵 \(e_{i, j}\) 表示当前 \(i\to j\) 是否有边。设 bfs 到 \((i, j)\)，则需要更新 \(i\) 可达 \(to\) 当且仅当 \(a_{i, to} = 0\) 且 \(e_{j, to} = 1\)。\(\lnot a_i\land e_j\) 即可找到所有 \(to\)。反图类似处理。

用 _Find_first 和 _Find_next 找 bitset 中第一个 \(1\) 和下一个 \(1\)，时间复杂度 \(\mathcal{O}(n ^ 3 / w)\)，是在稠密图上表现最优秀的算法。代码。

*CF1163F Indecisive Taxi Fee

修改一条边的权值相当于删去这条边的最短路和强制经过这条边的最短路的较小值。前者是删边最短路，后者也是容易的：

• 对于 \(e\in P\)，\(dis(1, n) - w_e + x\)。
• 对于 \(e\notin P\)，\(\min(dis(1, u_e) + w_e + dis(v_e, n), dis(1, v_e) + w_e + dis(u_e, n))\)。

时间复杂度 \(\mathcal{O}(m\log n + q)\)。代码。

类似题目：P1186 玛丽卡，P2685 桥。

*P7515 [省选联考 2021 A 卷] 矩阵游戏

神题。

\(nm\) 个未知数，\((n - 1)(m - 1)\) 个方程，还有不等式限制，一看就没法高斯消元。

既然如此，本题的突破口一定在 \(n + m - 1\) 个自由元上。首先让自由元的形态比较好考虑：钦定第一行和第一列上所有元素为自由元，固定它们为 \(0\)，根据 \(b\) 的限制推出剩下来整个矩阵 \(a_{i, j}\)。

考虑 \(a_{1, j}\)（\(j\geq 2\)），将其加上 \(1\)，发现会令所有 \(a_{i, j}\) 加上 \((-1) ^ {i - 1}\)。

考虑 \(a_{i, 1}\)（\(i\geq 2\)），将其加上 \(1\)，发现会令所有 \(a_{i, j}\) 加上 \((-1) ^ {j - 1}\)。

观察到 \(a_{i, j}\) 对应的不等式形成了 \(a_{1, j}\) 和 \(a_{i, 1}\) 之间的约束，很好。

但是对于 \(a_{1, 1}\)，它对整个矩阵产生的影响是这样的：

\[\begin{bmatrix}
1 & 0 & 0 & 0 & \cdots \\
0 & -1 & 1 & -1 & \cdots \\
0 & 1 & -1 & 1 & \cdots \\
0 & -1 & 1 & -1 & \cdots \\
\vdots & \vdots & \vdots & \vdots & \ddots
\end{bmatrix}
\]

这样一个约束有三个元素，无法处理。

但是根据之前的经验，将 \(a_{1, 1}\) 加上 \(1\) 可以理解为将所有 \(a_{1, j}\) 加上 \((-1) ^ {j - 1}\)，或将所有 \(a_{i, 1}\) 加上 \((-1) ^ {i - 1}\)。

这样，得到如下思路：设 \(r_i\) 表示将 \(a_{i, j}\) 加上 \((-1) ^ {j - 1} r_i\)，设 \(c_j\) 表示将 \(a_{i, j}\) 加上 \((-1) ^ {i - 1} c_j\)，那么调整后的 \(a'_{i, j} = a_{i, j} + (-1) ^ {j - 1} r_i + (-1) ^ {i - 1} c_j\)。当 \(i, j\) 奇偶性相同时，变量前的符号相同，无法处理。考虑写成 \(a_{i, j} + (-1) ^ {i + j} r_i - (-1) ^ {i + j} c_j\)，这样每个约束的两个变量符号相反，使用差分约束处理。

题目卡常，注意常数。SPFA 用最短路长度判无解会跑得快一些。

时间复杂度 \(\mathcal{O}(nm(n + m))\)。代码。

思考：\(r, c\) 共有 \(n + m\) 个变量，但自由元的数量只有 \(n + m - 1\)。多出来的自由度在哪里呢？注意到将 \(r\) 交替加减 \(x\)，\(c\) 交替加减 \(-x\)，得到的 \(a\) 相同。\(x\) 就是多出的自由度。

P2483 【模板】k 短路 / [SDOI2010] 魔法猪学院

\(k\) 短路模板题。不断求 \(k\) 短路，判断是否有累计权值大于 \(E\)。

代码。

2. 无向图最小生成树

本章讨论的图为 无向连通图。

关于有向图最小生成树（最小树形图），见 “图论 II”。

2.1 相关定义

• 生成树：对于连通图，形态是一棵树的生成子图称为 生成树。

通俗地说，生成树就是连通了图上所有点的树。非连通图不存在生成树。

• 生成森林：由每个连通分量的生成树组成的子图称为 生成森林。
• 非树边：对于某棵生成树，原图的不在生成树上的边称为 非树边。

生成树算法的核心思想：往生成树加入一条边形成环，考察环的性质。

给定一张带权连通图，求其边权和最小的生成树，称为 最小生成树（Minimum Spanning Tree，MST）。对于非连通图，对每个连通分量求最小生成树即得最小生成森林。

注意：连通图有最小生成森林，等于它的最小生成树。非连通图没有最小生成树。对任意图都可以求最小生成森林，但只有连通图才能求最小生成树。

2.2 最小生成树问题

介绍三种求最小生成树的算法。

2.2.1 Kruskal

考虑最终求得的生成树 \(T\)，考察其性质。

考虑一条非树边 \(e = (u, v, w)\)，以及生成树上连接 \(u, v\) 的简单路径。若 \(w\) 小于其中任意一条边的边权，将这条边从 \(T\) 中删去，再加入边 \(e\)，所得仍为生成树且权值变小。

这说明 \(T\) 满足：对于任意非树边 \((u, v, w)\)，树上连接 \(u, v\) 的简单路径上的每条边的权值不大于 \(w\)。这是 最小生成树的基本性质。

这启发我们将边按照边权从小到大排序，依次枚举每一条边，若当前边两端不连通则往生成树中加入该边。用并查集维护连通性，时间复杂度 \(\mathcal{O}(m\log m)\)。

若存在非树边 \(e = (u, v, w)\) 不满足上述性质，则考虑被替换的边 \(e' = (u', v', w')\) 其中 \(w' > w\)。因为考虑到 \(e'\) 时 \(u, v\) 不连通，所以考虑到 \(e\) 时 \(u, v\) 不连通，与 \(e\notin T\) 矛盾。

借助该工具，可以归纳证明加入的每一条边均在原图的最小生成树中。

并查集合并时新建虚点维护合并关系，得到 Kruskal 重构树。它刻画了在仅考虑权值不超过某个阈值的边时整张图的连通情况。见 “树论”。

2.2.2 Prim

维护当前点集 \(V\) 和边集 \(E\)，每次找到 \(\notin E\)，且一端 \(\in V\)，另一端 \(\notin V\) 的权值最小的边 \((u, v)\)，将 \(v\) 加入 \(V\)，\((u, v)\) 加入 \(E\)。初始 \(V\) 可以包含任意一个点，\(E\) 为空。

另一种理解方式：维护每个点的权值 \(c_v\) 表示 \(v\) 的所有邻边 \((v, u)\) 中，使得 \(u\in V\) 的最小权值。每次取出不在 \(V\) 中的权值最小的点加入 \(V\)，将最小生成树的边权加上 \(c_v\)（将对应边加入边集 \(E\)），并用 \(v\) 的邻边更新不在 \(V\) 中的点的权值。

“取出权值最小的点” 的过程类似 Dijkstra 算法借助优先队列实现。算法的时间复杂度为 \(\mathcal{O}(m\log m)\)。

Prim 算法的正确性证明和 Kruskal 差不多。

2.2.3 Boruvka

对于每个点 \(i\)，其权值最小的邻边必然在生成树上（若有多条，则任选一条）。否则将其加入 \(T\)，出现过点 \(i\) 的环，将环上对应的另一条邻边删去，得到权值更小的生成树。

对于每个点，求出边权最小的邻边。将这些边删去后加入最小生成树。除去至多 \(\lfloor\frac n 2\rfloor\) 条重边，每条边使连通分量数减 \(1\)，因此一轮这样的过程使得连通分量数严格减半。这样，对剩余连通分量继续上述操作至多 \(\log_2 n\) 轮，连通分量数为 \(1\)，即得最小生成树。

注意在选择边权最小的边时，不能选择两端已经在同一连通块的边：

• 对每个点，选择一端为该点，另一端和它不在同一连通块的权值最小的边。
• 对每个连通块，选择一端在该连通块，另一端不在该连通块的权值最小的边。

两种选边方式均正确，视情况使用更方便的一种。对于前者，总边数为 \(\mathcal{O}(n\log n)\)；对于后者，总边数为 \(\mathcal{O}(n)\)。

算法的时间复杂度为 \(\mathcal{O}(m\log n)\)。

Boruvka 在解决一类 MST 问题上非常有用：给定 \(n\) 阶完全图（任意两点间恰有一条边的无向图），边权通过某种方式计算。当 \(n\) 过大时，无法使用朴素 MST 算法，此时根据特殊的边权计算方式可以快速求出每个点权值最小的另一端不在该连通块的邻边，从而借助 Boruvka 算法做到复杂度与 \(m\) 无关。如例题 CF888G。

*2.3 拟阵和生成树

注：不保证本小节内容的严谨性。可跳过 2.3.1 和 2.3.2 直接阅读 2.3.3 小节的结论。

线性代数是研究图论问题的常见方法。当生成树和线性代数相结合，又会碰撞出怎样的火花呢？本小节简要介绍了拟阵，这个从线性代数中抽象出的概念，在生成树上的应用。

2.3.1 拟阵的定义与性质

拟阵的定义：记 \(M = (S, \mathcal {I})\) 表示拟阵，其中 \(\mathcal {I} \subseteq 2 ^ S\)，即 \(\mathcal {I}\) 是 \(S\) 的所有子集构成的集合的子集。\(S\) 中的元素称为 边，\(\mathcal {I}\) 中的元素称为 独立集，注意区分拟阵独立集和图独立集。\(M\) 需要满足以下两条公理：

• 遗传性：独立集的所有子集也是独立集。若 \(I\in \mathcal {I}\)，\(J\subseteq I\) 则 \(J\in \mathcal {I}\)。一般认为 \(\varnothing \in \mathcal {I}\)。
• 交换性：对于两个大小不同的独立集，存在仅属于较大的独立集的元素，使得较小的独立集加入该元素后仍为独立集。对于 \(I, J\in \mathcal {I}\)，若 \(|I| < |J|\)，那么存在元素 \(z\in J\backslash I\) 满足 \(I + \{z\}\in \mathcal {I}\)。

拟阵是对线性代数中 “线性无关” 的关系的抽象：对于向量集合 \(S\)，令 \(\mathcal {I}\) 为所有线性无关的向量集。那么遗传性可以理解为：任意线性无关向量集的子集也是线性无关的；交换性可以理解为：对于大小不同的向量集，较大的向量集的秩大于较小的向量集的秩，所以较大的向量集中总存在向量不能被较小的向量集表示。

拟阵和生成树的关系：令 \(S\) 为图的边集，它的子集 \(I\) 是独立集当且仅当 \(I\) 不存在环。证明 \((S, \mathcal {I})\) 是拟阵：

• 遗传性：一个边集无环，则该边集的子集显然无环。
• 交换性：设两个独立集 \(|I| < |J|\)，那么 \(I\) 形成的连通块数量大于 \(J\)。因此，总存在 \(J\) 形成的连通块，使得它在 \(I\) 上不连通。因此存在 \(J\) 的一条边在加入 \(I\) 时不会产生环。

由此构造的拟阵 \(M = (S, \mathcal {I})\) 被称为 图拟阵。

给出拟阵相关的若干重要定义：

• 基：对于独立集 \(I\)，若加入任何 \(S\backslash I\) 的元素都会变成非独立集，则称 \(I\) 是拟阵的一个 基，也称 极大独立集。
• 环：对于非独立集 \(I'\)，若删去其任何元素都会变成独立集，则称 \(I'\) 是拟阵的一个 环，也称 极小非独立集。

定理 1

基的大小相同。

证明

若存在两个大小不同的基 \(|A| < |B|\)，根据交换性，存在 \(z\in B\backslash A\) 使得 \(A + \{z\}\in \mathcal {I}\)，与基的定义矛盾。\(\square\)

定理 2（基交换定理）

设两个不同的基 \(A, B\)，对于任意 \(z\in A\backslash B\)，存在 \(y\in B\backslash A\) 满足 \(A - \{z\} + \{y\}\) 为 \(M\) 的基。

证明

因为 \(|A - \{z\}| < |B|\) 且 \(z\notin B\)，根据交换性，存在 \(y\in B\backslash (A - \{z\}) = B\backslash A\) 使得 \(A - \{z\} + \{y\}\in \mathcal {I}\)。\(\square\)

任意大小相同的不同独立集 \(I, J\) 之间都有交换定理（替换后仍为独立集），证明方法类似。笔者将对应的操作称为 \(I\to J\) 的单步替换。

图拟阵的每个基对应了 \(G\) 的一棵生成树，而基交换定理告诉我们，对于两棵不同的生成树 \(T, T'\)，删去 \(T\backslash T'\) 的任意一条边后，可以加入 \(T'\backslash T\) 的一条边使得它仍是一棵生成树。这给出了任意两个生成树之间的替换方案，其中单步替换为删去并加入一条边，满足替换过程中恒为生成树。

• 秩：基的大小称为拟阵的 秩，对于任意 \(S\) 的子集 \(U\)，定义 秩函数 \(r(U)\) 表示 \(U\) 的极大独立集（基）大小，即 \(\max_{I\in \mathcal {I}\land I\subseteq U} |I|\)。

可知 \(I\) 是 \(U\) 的基当且仅当 \(I\subseteq U\) 且 \(|I| = r(U)\)。容易证明 \(U\) 的基仍满足基交换定理。

秩函数 \(r\) 有如下性质：

• 有界性：\(\forall U\subseteq S, 0\leq r(U)\leq |U|\)。
• 单调性：\(\forall A\subseteq B\subseteq S, r(A)\leq r(B)\)。

\(r\) 的次模性在接下来研究的问题中并不重要，故略去。感兴趣的读者可自行查阅资料（专门学习拟阵时会写新的学习笔记）。

2.3.2 拟阵上的最优化问题

基交换定理很有用，它告诉我们拟阵的两个基可以通过替换元素相互得到。

通过上一小节的铺垫，我们可以解决拟阵上的最优化问题：给出定义在 \(S\) 上的函数 \(w: S\to \mathbb R\)，即 \(S\) 的每个元素 \(x\) 有权值 \(w(x)\)，求所含元素权值和 \(w(I) = \sum_{x\in I} w(x)\) 最大的独立集 \(I\)。

如果 \(I\) 包含权值非正的元素，根据遗传性，将这些元素删去后 \(I\) 仍为独立集，且权值不变小。因此 \(I\) 只包含权值为正的元素。

不妨设 \(S\) 的所有元素的权值均为正数，则 \(I\) 一定是 \(M\) 的一组基。否则，根据交换性，\(I\) 可以再添加元素使得权值增大。

为方便讨论，以下设元素权值均为 正整数。

拟阵的优秀性质启发我们尝试直接贪心：将 \(S\) 的元素按权值不升的顺序排序，得到 \(w(s_1) \geq w(s_2) \geq \cdots \geq w(s_{|S|})\)。依次考虑每个 \(s_i\)，若 \(I + \{s_i\}\in \mathcal {I}\)，则将 \(s_i\) 加入 \(I\)。

证明

设 \(I_i\) 表示考虑 \(s_i\) 之后 \(I\) 的形态，\(I'_i\) 表示最优解包含的下标不大于 \(i\) 的元素。设贪心结果 \(I\) 和最优解 \(I'\) 选择的元素下标分别为 \(\{x_i\}\) 和 \(\{y_i\}\)。

若存在 \(y_i < x_i\)，那么 \(I'_{y_i} \backslash I_{x_i}\) 只包含下标不大于 \(y_i\) 的元素（\(I'_{y_i}\) 只包含下标不大于 \(y_i\) 的元素）。进行 \(I_{x_i} \to I'_{y_i}\) 的单步替换，存在 \(s_z\in I'_{y_i}\backslash I_{x_i}\) 使得 \(I_{x_i} - \{s_{x_i}\} + \{s_z\}\in \mathcal {I}\)。则 \(z \leq y_i < x_i\) 且 \(z\notin I_z\)。而 \((I_z + \{s_z\})\subseteq (I_{x_i} - \{s_{x_i}\} + \{s_z\})\)，根据遗传性，\(I_z + \{s_z\}\in \mathcal {I}\)，这与 “能加入就加入” 的贪心算法矛盾。

故 \(x_i \leq y_i\)，即 \(w(s_{x_i}) \geq w(s_{y_i})\)，所以 \(w(I) \geq w(I')\)，\(I\) 一定是最优解。\(\square\)

扩展：如果要求权值最小，只需将元素按权值不降排序再贪心。

扩展：如果要求权值最大的 基，不要删去任何元素，直接做就行了。因为任意时刻 \(I\) 都是当前考虑到的所有元素的一组基。

证明

设 \(U_i = \{s_1, s_2, \cdots, s_i\}\)。

假设考虑到 \(s_i\) 时，\(I_i\) 不是 \(U_i\) 的基且 \(i\) 最小。因为 \(|I_i|\) 不会变小且 \(r(U_i)\) 至多增加 \(1\)，故只可能是 \(r(U_i) = r(U_{i - 1}) + 1\) 且 \(|I_i| = |I_{i - 1}|\)。

设 \(I'\) 为 \(U_i\) 的基，则 \(|I'| = r(U_i) > r(U_{i - 1}) = |I_{i - 1}|\)。根据交换性，存在 \(s_j\in I'\backslash I_{i - 1}\) 可以加入 \(I_{i - 1}\)。而 \(s_i\) 无法加入 \(I_{i - 1}\)，所以 \(j < i\)。因此 \(I_{i - 1} + \{s_j\}\in \mathcal {I}\) ，\(I_{i - 1}\) 不是 \(U_{i - 1}\) 的基，与 \(i\) 最小的假设矛盾。\(\square\)

从以上两条证明中可以总结出一个小套路：证明拟阵的性质，一般方法是反证 + 交换性和基交换定理。这有助于加深对拟阵的感性认知。

因为一张图的所有生成树也是拟阵，所以拟阵上的最优化问题的解法可以直接解决最小生成树问题。直接套用贪心过程，就得到了 Kruskal 算法。

2.3.3 最小生成树的性质

拟阵是研究最小生成树的强力工具。拟阵的贪心过程可以求得最小权基，但最小权基并不一定唯一。若要刻画所有最小权基的形态，研究它们共同具有的性质，就需要对贪心过程进行更深层次的探索。

一些问题需要将最小生成树的边权不超过某个值的边单独拎出来。请读者思考：在任意最小生成树中，所有权值不大于 \(w\) 的边具有什么样的共同特征？所有权值等于 \(w\) 的边呢？在贪心过程中，如果跳过了一些本可以加入生成树的边，是否仍能求出最小生成树？

如果你觉得这个问题比较困难，可以先思考特殊情况：所有元素的权值互不相同。

结论

若所有元素的权值互不相同，则最小权基唯一。

证明

假设存在两个最小权基 \(I, I'\)。按权值从小到大排序后，设 \(I\) 和 \(I'\) 选择的元素下标分别为 \(\{x_i\}\) 和 \(\{y_i\}\)。

因为 \(I\neq I'\)，所以存在 \(i\) 使得 \(x_i\neq y_i\)。找到最大的 \(i\)，不妨设 \(y_i < x_i\)，那么 \(I'\backslash I\) 包含的元素下标不大于 \(y_i\)。进行 \(I\to I'\) 的单步替换，存在 \(z \leq y_i < x_i\) 使得 \(J = I - \{s_{x_i}\} + \{s_z\}\in \mathcal {I}\)。因为元素权值互不相同，所以 \(w(s_z) < w(s_{x_i})\)，故 \(w(J) < w(I)\)，与 \(I\) 是最小权基矛盾。\(\square\)

借助相同的思想，可以证明如下性质：

结论

对于权值 \(w\)，设权值不大于 \(w\) 的元素集合为 \(U_w\)，则对于任意最小权基 \(I\)，\(I\) 包含的权值不大于 \(w\) 的元素个数为 \(r(U_w)\)。

证明

设两个最小权基 \(I\neq I'\)。对它们不断应用最小权唯一时的替换方法（可能是 \(I\to I'\) 的单步替换，也可能是 \(I'\to I\) 的单步替换，取决于 \(x_i\) 和 \(y_i\) 的大小关系），则 \(w(I), w(I')\) 均不增加。又因为 \(w(I), w(I')\) 是最小权基，所以 \(w(I), w(I')\) 不减少。所以每次替换时删去和加入的元素权值相同。这说明任意两个最小权基在相互替换直到相等的过程中，权值等于某个值的元素数量不变，所以任意最小权基的权值等于某个值的元素个数相等。

再根据贪心过程得到的最小权基包含的权值不大于 \(w\) 的元素个数为 \(r(U_w)\)，得证。\(\square\)

推论

对于每个权值 \(w\)，任意最小权基含有的权值不大于 \(w\) 和等于 \(w\) 的元素个数为定值。

推论

对于每个权值 \(w\)，任意最小生成树含有的权值不大于 \(w\) 和等于 \(w\) 的边的个数为定值。

在图拟阵中，集合 \(U\) 的一组基表示在仅保留 \(U\) 对应的边时，整张图的一棵生成森林。那么上述性质告诉我们：在任意最小生成树中，仅保留权值不大于 \(w\) 的边时，整张图的连通性相同。即若 \(u, v\) 通过权值不大于 \(w\) 的边连通，那么在任意最小生成树中，它们也可以通过权值不大于 \(w\) 的边连通。

可以感受到，在最小生成树中，每个权值的边相对独立。求最小生成树的过程可以看做：从小到大枚举所有权值。将已经加入的边的两端缩成一个点，求当前权值的边的任意一棵生成森林，并将这些边加入最小生成树。所有最小生成树都可以通过该过程生成，且每层 “当前权值的边” 的生成森林的多样性导致了最小生成树的多样性。

重要事实：将最小生成树 \(T\) 的权值不等于 \(w\) 的边的两端缩成一个点，最小生成树的权值等于 \(w\) 的边的形态，就是这张图的任意一棵生成树。注意这不意味着两个最小生成树 \(T\) 和 \(T'\) 关于权值不等于 \(w\) 的边的缩点图相等。反例：\(G = \{(1, 2, 1), (1, 3, 2), (2, 3, 2)\}\)，\(T = \{(1, 2, 1), (1, 3, 2)\}\)，\(T' = \{(1, 2, 1), (2, 3, 2)\}\)，它们关于权值 \(1\) 的缩点图，一张 \(1, 3\) 缩在一起，另一张 \(2, 3\) 缩在一起。

实际上，将权值大于 \(w\) 的边的两端也缩在一起，只是为了把权值为 \(w\) 的边关于权值小于 \(w\) 的边的缩点图的生成森林连起来变成生成树。这样在最小生成树计数时方便些：对最小生成森林计数，需要对每个连通块分别求最小生成树的数量并相乘，较麻烦。处理后只要求缩点图的生成树，若缩点图不连通说明原图不连通，生成树数量为 \(0\)，不必对每个连通块单独求最小生成树的数量。

此外，点对 \((u, v)\) 第一次连通时对应的权值 \(w\)，就是它们之间所有路径的边权最大值的最小值，即 \(u, v\) 之间必须经过权值不小于 \(w\) 的边，且恰存在一条路径使得边权不大于 \(w\)。Kruskal 重构树刻画了像这样的关于边权的连通性，见 “树论”。

2.4 扩展问题

除了以下提到的扩展问题，还有使用 LCT 维护生成树的经典手段：在生成树上加入一条边，先求出这条边两端的路径上的权值最大的边，将最大边从生成树中删去，再加入当前边。

2.4.1 次小生成树

注：可以不看证明只看结论。

问题描述：求次小生成树的权值。次小生成树即权值第二小的生成树。

感性理解，如果次小生成树和最小生成树相差很多边，可以用基交换定理调整成只相差一条边。而只相差一条边是好做的：枚举每条非树边，求出其两端对应路径上权值最大的边，得到替换后生成树的最小权值。所有替换方案的最小权值对应的生成树就是次小生成树。

倍增求路径最大边权，时间复杂度 \(\mathcal{O}(n\log n)\)。

结论

对于任意最小生成树 \(T\)，若存在次小生成树 \(T'\)，则存在次小生成树 \(T'\) 使得 \(T\) 和 \(T'\) 只相差一条边。

证明

设 \(T\) 和 \(T'\) 包含的边的编号为 \(\{x_i\}\) 和 \(\{y_i\}\)，其中边按权值不降排序。存在最大的 \(i\) 使得 \(x_i\neq y_i\)。

如果 \(w(y_i) < w(x_i)\)，进行 \(T\to T'\) 的单步替换，得到权值更小的生成树，矛盾。

否则 \(w(y_i) \geq w(x_i)\)，进行 \(T'\to T\) 的单步替换，得到权值不大于 \(w(T')\)，且与 \(T\) 相差边数减少 \(1\) 的生成树。

因此，如果 \(T'\) 与 \(T\) 相差大于一条边，总可以调整使得权值不增，且恰与 \(T\) 相差一条边。\(\square\)

这个结论对严格次小生成树仍然适用。严格次小生成树即权值严格大于 \(w(T)\) 的权值最小的生成树。

结论

对于任意最小生成树 \(T\)，若存在严格次小生成树 \(T'\)，则存在严格次小生成树 \(T'\) 使得 \(T\) 和 \(T'\) 只相差一条边。

证明

次小生成树的证明不再适用，因为调整过程中可能出现 \(w(T') = w(T)\)。

欲证结论，只需证明对任意非最小生成树 \(T'\)，可以从 \(T'\) 不断调整，每次调整不增加权值，得到与 \(T\) 相差一条边的生成树。结论的证明较复杂，但这是笔者能想到的最简单的证明。如果有更简洁的证明欢迎交流。

引理（强基交换定理）

设两个不同的基 \(A, B\)，对于任意 \(x\in A\backslash B\)，存在 \(y\in B\backslash A\)，使得 \(A - \{x\} + \{y\}\) 和 \(B - \{y\} + \{x\}\) 均为 \(M\) 的基。

证明较复杂，略去。

设 \(T\) 和 \(T'\) 包含的权值为 \(i\) 的边集分别为 \(\{X_i\}\) 和 \(\{Y_i\}\)。不断应用次小生成树的证明，直到某一步 \(y_p\to x_p\) 使得 \(w(T') = w(T)\)。在这一步之前停下。因为最小生成树的每个权值的边数固定，所以：

• 存在 \(j < i\) 满足 \(|Y_j| + 1 = |X_j|\)，\(|Y_i| - 1 = |X_i|\)。
• 对于任意 \(k\neq i, j\)，有 \(|X_k| = |Y_k|\)。
• 对于 \(k > i\)，有 \(X_k = Y_k\)（否则不会选中 \(y_p\)）。

考虑 \(k = i\)：对 \(x\in X_i\backslash Y_i\) 用强基交换定理，存在 \(y\in T'\backslash T\) 使得 \(T - \{x\} + \{y\}\in \mathcal {I}\)。因为 \(X_k = Y_k\)（\(k > i\)），所以 \(w(y)\leq w(x)\)。因为 \(T\) 是最小生成树，所以 \(w(y)\geq w(x)\)。因此 \(w(y) = w(x)\)，即 \(y\in Y_i\backslash X_i\)。根据强基交换定理，令 \(T'\) 变成 \(T' - \{y\} + \{x\}\)。不断进行该操作直到 \(X_i\backslash Y_i\) 为空，此时 \(Y_i\) 等于 \(X_i\) 加上一个元素。

从 \(i - 1\) 到 \(j + 1\) 降序枚举 \(k\)：归纳假设对于所有 \(k' > k\)，恰存在一个 \(k'\) 满足 \(Y_{k'}\) 等于 \(X_{k'}\) 加上一个元素，设为 \(p\)，且对于其它 \(k'\) 有 \(Y_{k'} = X_{k'}\)。类似 \(k = i\) 的情况，对 \(x\in X_{k}\backslash Y_k\) 使用强基交换定理直到 \(X_k \backslash Y_k\) 为空。过程中可能删去了 \(Y_p\) 多出来的元素，此时 \(Y_k\) 等于 \(X_k\) 加上一个元素，新的 \(p\) 变成当前的 \(k\)；也可能没有删掉，此时 \(Y_k = X_k\)。归纳假设仍然成立。

经过上述调整，有：

• 存在 \(j < i\) 使得 \(|Y_j| + 1 = |X_j|\)，\(|Y_i| - 1 = |X_i|\)，且 \(Y_i\) 为 \(X_i\) 加上一个元素（即 \(X_i\subset Y_i\)）。
• 对于 \(k < j\)，有 \(|X_k| = |Y_k|\)。
• 对于 \(i < k < j\) 和 \(k > j\)，有 \(X_k = Y_k\)。

此时 \(T\backslash T'\) 不存在权值大于 \(j\) 的元素。

从 \(j\) 到 \(1\) 降序枚举 \(k\)：归纳假设 \(T\backslash T'\) 不存在权值大于 \(k\) 的元素，且对于 \(k' < k\)，有 \(|X_{k'}| = |Y_{k'}|\)。对 \(y\in Y_k\backslash X_k\) 进行 \(T'\to T\) 的单步替换。假设选择 \(x\in T\backslash T'\)。因为 \(T\backslash T'\) 不存在权值大于 \(k\) 的元素，所以 \(w(x) \leq k\)。而如果 \(w(x) < k\)，则根据遗传性，替换后 \(T'\) 的所有权值不大于 \(w(x)\) 的元素形成独立集，且元素个数为 \(T\) 的权值不大于 \(w(x)\) 的元素的个数加 \(1\)。这和 “\(T\) 的所有权值不大于 \(w(x)\) 的元素为 \(S\)（拟阵的边集）的所有权值不大于 \(w(x)\) 的元素的基” 矛盾。因此 \(w(x) = k\)。不断进行操作直到 \(Y_k\backslash X_k\) 为空，此时 \(X_k = Y_k\)（\(k < j\)）或 \(X_k\) 为 \(Y_k\) 加上一个元素（\(k = j\)）。归纳假设仍然成立。

最终我们得到：

• 存在 \(j < i\) 使得 \(X_j\) 为 \(Y_j\) 加上一个元素，\(Y_i\) 为 \(X_i\) 加上一个元素。

• 对于任意 \(k\neq i, j\)，\(X_k = Y_k\)。

这说明 \(T\) 和 \(T'\) 之间只相差一条边，且 \(w(T) < w(T')\)。而显然地，调整的每一步 \(w(T')\) 不增。\(\square\)

如果从 “最小生成树的权值不大于 \(w\) 的边的连通性相同” 入手，可以在一开始将 \(Y_{1\sim j - 1}\) 全部替换为 \(X_{1\sim j - 1}\)，替换后的 \(T'\) 仍为生成树。因为 \(\bigcup X_{1\sim j - 1}\) 是拟阵的权值不大于 \(j - 1\) 的元素的基，而 \(X_k = Y_k\)，所以 \(\bigcup Y_{1\sim j - 1}\) 也是一组基。基就意味着它们的连通性和拟阵的权值不大于 \(j - 1\) 的所有边的连通性相同。

可以类似推导出任意拟阵存在次小权基和严格次小权基（若存在）与最小权基只有一个元素不同。实际上我们已经证明了这一点：上述两条结论的证明用到的所有关于最小生成树的结论都是由拟阵本身得出的，故适用于所有拟阵。将证明中的 “最小生成树” 改成 “独立集” 即可。

例题：P4180。

2.4.2 最小生成树计数

问题描述：求一张图的最小生成树的数量。

前置知识：生成树计数（矩阵树定理）。

根据 2.3.3 小节提到的性质，从小到大枚举边权 \(w\)，求出将所有权值小于 \(w\) 的边的两端缩起来后，边权为 \(w\) 的边的生成森林个数，然后将属于同一连通块的点缩起来。

求生成森林个数有些麻烦。2.3.3 小节最后提到，可以先求出任意最小生成树，将生成树上权值不等于 \(w\) 的边的两端缩起来，再使用矩阵树定理求出所有权值等于 \(w\) 的边关于缩点图的最小生成树的数量。

注：最小生成树计数和最小生成森林计数的不同点在于，对于非连通图，前者的答案为 \(0\)，后者的答案为每个连通块的最小生成树的数量之积。

复杂度分析：设最小生成树有 \(c_w\) 个权值为 \(w\) 的边，那么考虑边权 \(w\) 时，点的数量为 \(c_w + 1\)。而 \(\sum c_w \leq n\)，所以 \(\sum (c_w + 1) ^ 3 \leq \sum (c_w + 1) n ^ 2 = (\sum c_w + 1) n ^ 2 \leq 2n ^ 3\)。时间复杂度为 \(\mathcal{O}(n ^ 3)\)。

例题：P4208。

*2.4.3 \(k\) 小生成树

和 \(k\) 短路是类似问题，学会其中一个之后容易理解另一个。

问题描述：求无向带权简单图前 \(k\) 小生成树的权值。例题。

首先求出最小生成树。

已知次小生成树可由最小生成树加入一条非树边并删去一条树边得到。枚举非树边 \((u, v)\)，求出 \(u, v\) 在最小生成树的简单路径上权值最大的边，如果加入 \((u, v)\)，则删去这条边。对每条非树边求出加入它对权值的影响是多少，取权值增加量最小的方案。

对最小生成树求出权值增加量最小的非树边，则有两种选择：强制选择这条边，和强制不选择这条边。对于前者，给出了一棵新的生成树；对于后者，没有给出新的生成树，但边的状态改变了。

如果强制不选择这条边，那么接下来就是决策权值增加量次小的边是否强制选择，依次类推。于是最小生成树给出了若干棵新的生成树，其中第 \(i\) 棵生成树钦定了权值增加量前 \(i - 1\) 小的非树边不选择，且第 \(i\) 小的非树边强制选择。将所有生成树加入优先队列。

不断从优先队列取出权值最小的生成树 \(k\) 次做上述扩展，注意已经钦定状态的边不可被改变。一条边有四种状态：树边且可被替换；非树边且可加入生成树；树边且不可被替换；非树边且不可加入生成树。在枚举所有非树边时需要跳过所有不可加入生成树的非树边，求一条非树边能替换掉哪条树边时不能替换不可被替换的树边。

为什么这样做是对的：钦定权值增加量最小的非树边是否选择，本质是将当前生成树可扩展到的生成树集合分裂为了两半，一半含这条非树边，另一半不含这条非树边。每棵可扩展到的生成树恰属于其中一半。对于含非树边的，替换后的生成树一定是这些生成树的权值最小值，因为替换后的生成树是相对于当前生成树而言的次小生成树，即不存在可扩展到的生成树的权值小于替换后的生成树（否则和替换后的生成树为次小生成树矛盾了）。对于不含非树边的，对应集合的最小值依然是当前生成树，但一条非树边的状态从可加入变成了不可加入。

如果将每棵生成树抽象为一个点，用一棵有根树描述整个扩展过程（根节点是最小生成树），那么每个非叶子结点有两个儿子，一个是实点，从当前点向下走到实点表示用一条非树边替换了一条树边得到新的生成树；另一个则是虚点，从当前点向下走到虚点表示当前生成树的一条非树边从可加入变成了不可加入。由于实点一定是当前生成树能扩展到的最小生成树，所以整个过程是不重不漏的。

支持对一个 “点” 求权值增加量最小的非树边：直接求树链最值需要倍增，但我们只需求 \(\mathcal{O}(k)\) 次权值增加量最小的非树边。考虑对每条可被替换的树边求出能替换它的权值最小的非树边，操作方式为按权值从小到大的顺序枚举可以加入的非树边，将对应路径上所有还没被标记的边标记。可以用并查集实现该过程。

优先队列中不需要存储生成树的具体形态，只需记录每棵生成树由哪棵生成树如何替换一条边扩展得到，以及权值。等到真正取出这棵生成树之后再对其 DFS 预处理相关信息（以支持求权值增加量最小的非树边）。

此外，为了避免从优先队列中不断取出虚点导致求了 \(\mathcal{O}(m)\) 次后继状态（相当于去掉了所有虚点，将二叉树变成了多叉树，一次扩展所有儿子），考虑只扩展一次且只维护实点，并在取出实点后加入它的 “兄弟虚点” 的实儿子。

时间复杂度 \(\mathcal{O}(m\log m + mk\alpha(n) + k\log k)\)。代码。

*2.4.4 最小度限制生成树

问题描述：给定 \(k\)，求点 \(1\) 的度数为 \(k\) 的最小生成树。

该问题有 \(\mathcal{O}(m\log V\alpha (m))\) 的 wqs 二分做法，不在本文讨论范围内，感兴趣的同学可自行查阅资料。

先求出不含点 \(1\) 的最小生成森林 \(T\)，则不在森林上的边一定无用。

证明

设 \(e = (u, v, w)\) 为非树边，根据最小生成树的基本性质，存在连接 \(u, v\) 的树边构成的路径 \(P\)，且路径上每条边的权值不大于 \(w\)。

假设 \(e\) 在最小 \(k\) 度生成树上，断开 \(e\)，\(u, v\) 不连通。因此 \(P\) 上存在一条边使得其两侧不连通，加入该树边即可。\(\square\)

设 \(2\sim n\) 每个点的点权为它和 \(1\) 之间的边权，若不存在则为 \(+\infty\)。考虑最终生成树，将 \(1\) 删去后整张图裂成 \(k\) 个连通块，每个连通块会选择与 \(1\) 相连的权值最小的边，即点权最小值。故一棵最小生成树可理解为：从 \(T\) 删去若干条边，使图分裂为 \(k\) 个连通块。在每个连通块中选择权值最小的点与 \(1\) 相连。这样，可以用只含 \(2\sim n\) 的森林描述最小 \(k\) 度生成树。

\(T\) 初始的连通块数量决定了度数的下界，而点权不为无穷大的点的数量决定了度数的上界。为方便讨论，以下设 \(T\) 连通且 \(1\) 和每个点均有边，则最小 \(1\sim n - 1\) 度生成树均存在。

最小生成树可以贪心，那么最小 \(k\) 度生成树是否也可以贪心呢？能否每次贪心地删去一条树边，使得 \(w(T') - w(T)\) 最小？

考虑删去树边 \(e\) 后树的权值如何变化：设删去 \(e\) 前 \(e\) 所在连通块为 \(C\)，最小权点为 \(x\)。删去 \(e\) 后 \(C\) 分裂为两个连通块 \(C_1, C_2\)，不妨设 \(x\) 是 \(C_1\) 的最小权点，同时设 \(C_2\) 的最小权点为 \(y\)，则权值变化量为 \(f(e) = w(T') - w(T) = w(y) - w(e)\)。

结论

对于初始最小生成树 \(T\)，考虑使得 \(f(e)\) 最小的边 \(e\)。对于任意 \(2\leq k < n\)，存在最小 \(k\) 度生成树 \(T_k\) 删去了 \(e\)。

证明

设 \(x, y\) 分别为删去 \(e\) 后两个连通块 \(C_1, C_2\) 的最小权点，其中有一个是 \(T\) 的最小权点，设为 \(x\)，则 \(x\) 在任何连通块内都是最小权点，所以 \(x\) 一定被选中。

根据 \(f(e)\) 的最小性，\(e\) 一定是 \(T\) 的连接 \(x, y\) 的路径 \(P\)（\(P = p_0(x)\to p_1 \to \cdots \to p_c(y)\)）上的最大权边。

假设 \(e\in T_k\) 并从 \(T_k\) 中删去点 \(1\)，设包含 \(e\) 的连通块为 \(C\)。

• 若 \(y\) 被选中：因为 \(x, y\) 均被选中，所以它们在 \(T_k\) 上不连通。设 \(P\) 和 \(C\) 的交集为路径 \(Q\)。因为 \(e\in Q\)，所以 \(Q\) 非空，设为 \(p_l\rightsquigarrow p_r\)（\(0\leq l < r\leq c\)）。

  • 若 \(C\) 被选中的点在 \(e\) 左侧（含有 \(x\) 一侧的子树），则 \(y\notin C\)（因为 \(y\) 也被选中），即 \(r < c\)。加入边 \((p_r, p_{r + 1})\)，删去 \(e\)，考虑权值变化：

    • 因为 \(e\) 是 \(P\) 的最大权边，所以 \(w(e) \geq w(p_r, p_{r + 1})\)。
    • 因为 \(C\) 被选中的点不变，其它连通块没有缩小，所以被选中的点的权值之和不增。

    这说明调整后权值不增。

  • 若 \(C\) 被选中的点在 \(e\) 右侧（含有 \(y\) 一侧的子树），则 \(x\notin C\)，即 \(0 < l\)。加入边 \((p_{l - 1}, p_l)\)，删去 \(e\)，类似可证权值不增。

• 若 \(y\) 未被选中：因为 \(y\) 是 \(e\) 右侧的最小权点，所以 \(y\) 所在连通块一定包含 \(e\) 左侧的点，因此 \(y\in C\)。设任意一条与 \(x\) 所在连通块 \(C_x\) 相连的被删去的边为 \(e'\)（因为 \(k\geq 2\)，所以 \(e'\) 存在），它连接的另一个连通块 \(C'\) 的最小权点为 \(y'\)。在原树 \(T\) 中删去 \(e\) 后，另一个连通块 \(C''\) 包含 \(C'\)，所以 \(C''\) 的最小点权不大于 \(w(y')\)，因此 \(f(e') \leq w(y') - w(e')\)。

  加入边 \(e'\)，对权值的影响为 \(w(e') - w(y')\)。然后删去 \(e\)。因为 \(C\) 的最小权点在 \(y\) 左边，所以 \(C\) 分裂出的两个连通块 \(C_1, C_2\)，一个的最小权点为 \(C\) 最小权点，另一个包含 \(y\)，最小点权不大于 \(w(y)\)，对权值的影响不大于 \(w(y) - w(e) = f(e)\)。而 \(f(e) \leq f(e') \leq w(y') - w(e')\)，因此权值不增。

综上，总可以调整使得 \(T_k\) 权值不增且 \(e\notin T_k\)。\(\square\)

因此，在求最小 \(2\leq k < n\) 度生成树之前，可直接将 \(f(e)\) 最小的 \(e\) 删去。注意到删去后两个子树的贡献独立，结合上述结论，我们猜测每个点的贡献都是独立的。

设 \(f_k(T)\)（\(1\leq k\leq |T|\)）表示当初始树为 \(T\) 时（不含点 \(1\)），它的最小 \(k\) 度生成树的权值。设 \(T_k\) 表示对应连通块形态（不含点 \(1\)）。即从 \(T\) 删去 \(k - 1\) 条边，使其裂成 \(k\) 个连通块，所有边权加上每个连通块最小点权的最小值，以及取到最小值时的形态。

结论

对于 \(2\leq k \leq |T|\) 和任意 \(T_{k - 1}\)，存在 \(T_k\) 为 \(T_{k - 1}\) 删去一条边，且 \(f_{k}(T)\) 关于 \(k\) 在 \([1, |T|]\) 上下凸。

证明

当 \(|T| = 1\) 或 \(2\) 时显然成立。

若 \(|T| > 2\)，根据上述结论，设使得删去后新的权值最小的边为 \(e\)（不一定是权值最小的边），可钦定 \(T_{2\sim |T|}\) 一定删去 \(e\)。

设删去 \(e\) 后得到的两棵树为 \(T'\) 和 \(T''\)，归纳假设 \(T'\) 和 \(T''\) 满足结论。

因为 \(T\) 和 \(T''\) 的贡献独立，所以 \(f_k(T)\) 等于 \(f_{k_1}(T') + f_{k_2}(T'')\) 的最小值，其中 \(1\leq k_1 \leq |T'|\)，\(1\leq k_2\leq |T''|\)，且 \(k_1 + k_2 = k\)。这是下凸函数的 \(\min +\) 卷积，根据经典理论（闵可夫斯基和），\(f_k\) 也是下凸的。而 \(f_{k_1}(T')\) 和 \(f_{k_2}(T'')\) 的每个差分值都对应 “删去一条边产生的贡献”，所以 \(f_k(T)\) 的每个差分值都对应 “从 \(T'\) 或 \(T''\) 中删去一条边产生的贡献”。

另一种理解方式：结论实际上说明了在 \(T_1\to T_2\to \cdots \to T_{|T|}\) 的过程中，每次删去一条使得新的权值最小的边，且权值变化量（每条边的代价）随着删边而不降（下凸即二阶导非负，\(f_{k + 1}(T) - f_{k}(T)\geq f_k(T) - f_{k - 1}(T)\)）。现在 \(T\) 分裂成 \(T'\) 和 \(T''\)，因为 \(T'\) 和 \(T''\) 独立，所以删去使得新的权值最小的边相当于初始令 \(k_1, k_2 = 1\)，每次选择 \(f_{k_1 + 1}(T') - f_{k_1}(T')\) 和 \(f_{k_2 + 1}(T'') - f_{k_2} (T'')\) 较大的那个差分值，令其为 \(f_{k + 1}(T) - f_k(T)\)，然后将 \(k\) 和被选中的 \(k_i\) 加上 \(1\)。

此时只需证明 \(f_2(T) - f_1(T) = f(e)\leq f_3(T) - f_2(T)\)。

可以证明在子图上删去一条边的代价不小于在原图上删去这条边的代价：设在原图删去 \(e'\) 之后，不含 \(x\) 的连通块为 \(C\)，新增点权为 \(C\) 的最小点权 \(w(C)\)。在子图删去 \(e'\) 之后，一定有一侧连通块 \(C'\) 包含于 \(C\)。新增点权为两侧连通块最小点权的较大值，不小于 \(C'\) 的最小点权 \(w(C')\)。而 \(C'\subseteq C\)，所以 \(w(C) \leq w(C')\)。

结合 \(f(e)\) 的最小性，得证。\(\square\)

上述结论告诉我们，随着 \(k\) 增大，已经删去的边不会再出现，已经加入的点不会再消失。

至此，存在 \(n ^ 2\) DP 做法：对每个连通块以最小权点为根 DFS，求出每个子树的最小点权，可知删去每条边的权值变化量。取代价最小的边删去即可。

若删去 \(e\) 后新增点 \(y\)，则称 \(e\) 被 \(y\) 删去。根据结论，每条边被固定的点删去。考虑求出 \(e\) 被哪个点删去。

设删去 \(e\) 之前所在连通块的最小权点为 \(x\)，则 \(e\) 在 \(x, y\) 的路径上，且 \(e\) 是路径边权最大值（对边权相同的边任意钦定大小关系，不影响答案）。设 \(C\) 为包含 \(e\) 的权值不大于 \(w(e)\) 的边形成的连通块，考察 \(C\) 的状态。

注意到对于 \(x', y'\) 至少一个不属于 \(C\) 的操作，\(C\) 中不可能有边被删掉，因为 \(x', y'\) 之间的路径如果经过 \(C\)，那么一定经过权值大于 \(w(e)\) 的边（由 \(C\) 的定义可知）。这说明当 \(C\) 的第一条边被删去时，一定有 \(x', y'\in C\) 且 \(x' = x\)。

设 \(C_x\) 为 \(e\) 的 \(x\) 一侧与 \(C\) 的交，另一侧为 \(C_y\)。设 \(y_{\min}\) 为 \(C_y\) 的最小权点。设 \(x', y'\) 删去的边为 \(e'\)。

• 如果 \(y'\in C_y\)，则 \(x', y'\) 路径上的最大权边为 \(e\)，得 \(e' = e\)，推出 \(y' = y_{\min}\)。
• 如果 \(y'\in C_x\)，则 \(w(e') < w(e)\)（\(e\) 是 \(C\) 的最大边权），根据 \(w(y') - w(e')\) 的最小性得 \(w(y') < w(y_{\min})\)。新的 \(x\) 有可能变为 \(y'\)，但无论何种情况点权均不大于 \(y_{\min}\)。

因此 \(y = y_{\min}\)，即 \(e\) 一定被 \(y_{\min}\) 删去。

在 Kruskal 的过程中维护连通块的最小点权。用 \(e\) 合并两个连通块时，可求出删去 \(e\) 产生的贡献 \(c(e)\) 等于最小点权的较大值减去 \(w(e)\)。将 \(e\) 按 \(c(e)\) 从小到大排序得 \(e_{1\sim n - 1}\)，则 \(f_{k + 1}(T) = f_{k}(T) + c(e_k)\)。

最后处理遗留的细节：之前钦定了 \(T\) 连通且 \(1\) 与 \(2\sim n\) 每个点相连。对于 \(T\) 不连通的情况是一样的，因为 \(T\) 的每个连通块独立，连通块数决定了最小的 \(k\)，对小于 \(k_{\min}\) 的 \(k\) 无解。如果权值为正无穷，说明 \(k\) 超过上界（上界为初始连通块数，加上 \(c\) 值不为正无穷的边数），同样无解。

算法在 \(\mathcal{O}(m\log m)\) 的时间复杂度内，对每个 \(1\leq k \leq n - 1\) 判定最小 \(k\) 度生成树是否存在，若存在则可以求出其权值。

模板题 的 代码。

2.5 例题

P1967 [NOIP2013 提高组] 货车运输

求出最大生成树，那么使得 \(u, v\) 第一次连通的边就是 \(u, v\) 之间所有路径边权最小值的最大值。它等于 \(u, v\) 在最大生成树上的简单路径边权最小值。倍增即可。

设 \(n, m\) 同级，时间复杂度 \(\mathcal{O}((n + q)\log n)\)。代码。

P4180 [BJWC2010] 严格次小生成树

因为总可以调整使得严格次小生成树和最小生成树之间只差一条边，所以先求出任意最小生成树，然后枚举非树边，加入该边之后替换掉环上比该非树边权值小的权值最大的边，为原树一条路径上权值最大或严格第二大的边。

倍增即可，时间复杂度 \(\mathcal{O}(m\log n)\)。代码。

P4208 [JSOI2008] 最小生成树计数

最小生成树计数的板子题。因为相同权值的边不超过 \(10\) 条，如果你不会 Matrix-Tree 定理，也可以直接枚举边集检查是否为最小生成树。

模数不为质数，需要使用辗转相除式的行列式求值。

时间复杂度 \(\mathcal{O}(n ^ 3)\)。代码。

*CF888G Xor-MST

根据异或不难想到对 \(a_i\) 建出 01 Trie。

对于 01 Trie 上某个状态 \(p\) 的子树包含的所有结点 \(V_p\)，它们之间已经连通：\(V_p\) 跨过该状态向其它状态 \(q\) 所表示的结点 \(V_q\) 连边的代价大于在 \(V_p\) 内部连边的代价。因为跨过连边时，代价在 \(p\) 对应位或其高位有值，但内部连边时 \(p\) 对应位及其高位没有值。整个过程类似 Kruskal 算法。

考虑计算答案。若 \(p\) 的左右儿子内均有结点，那么需要在 \(V_{ls_p}\) 和 \(V_{rs_p}\) 之间连一条边使得 \(V_p\) 连通。枚举 \(V_{ls_p}\) 中所有权值 \(v\) 并求出 \(rs_p\) 的子树中与 \(v\) 异或和最小的权值 \(u\)，那么 \(u\oplus v\) 的最小值即为连边代价。

因为一个结点最多被枚举 \(\log V\) 次，所以即使不启发式合并，时间复杂度也可以接受，为 \(\mathcal{O}(n\log ^ 2 V)\)。若启发式合并，则复杂度为 \(\mathcal{O}(n\log n\log V)\)。代码。

*CF1305G Kuroni and Antihype

这题就很厉害了。

先假设存在一个邀请方案，分析它的一般性质。

将邀请的操作视为有根树森林，每个点由它的父亲邀请而来，则总贡献为每个点的权值乘以它的儿子数量。对于除了根以外的节点，它的儿子个数为它的度数 \(-1\)。那么我们有没有什么办法让根节点也满足这样的性质呢？很简单，用一个权值为 \(0\) 的虚点连向所有根，这样总贡献严格符合每个点的权值乘以度数 \(-1\)，且森林变成了一棵树。

将总贡献加上每个点的权值，这是一个定值，则我们希望最大化每个点的权值乘以度数。度数启发我们将每个点的贡献摊到与它相邻的边上，每条边的贡献即它的两端的权值之和。对原图求最大生成树（注意包含点 \(0\)，\(a_0 = 0\)），其权值减去每个点的权值之和即为答案。

考虑 Kurskal，从小到大枚举边权 \(i\) 及其子集 \(j\)，将所有权值为 \(j\) 的点和权值为 \(i - j\) 的点连成一个连通块。时间复杂度 \(\mathcal{O}(3 ^ k)\)，其中 \(k = \lceil\log_2 n\rceil\)。代码。

考虑 Boruvka，我们需要找到一个连通块向外的最小边权。考虑高维前缀和，对每个 mask 维护权值是它的子集的最大点权以及对应点编号，但这样在查询一个点权值补集的信息时，点权最大的点可能和该点在同一连通块。因此，对每个 mask，我们还要维护权值是它子集且不与权值最大点在同一连通块的次大点。写起来细节较多，但时间复杂度更优，为 \(\mathcal{O}(2 ^ k\log ^ 2n)\)。代码。

CHANGE LOG

• 2025.7.14 修改部分错误。

---

参考资料

定义

• 图论相关概念 —— OI Wiki。
• 图论概念梳理 —— OI 中转站。

第一章

• Dijkstra 算法描述及正确性证明 —— ciwei。
• Floyd 算法正确性 —— dypdypdyp123。
• 【图论】传递闭包的概念 —— zkq_1986。
• 删边最短路问题 —— dengyaotriangle。
• 堆的可持久化 —— 俞鼎力。
• 可持久化线段树求 k 短路 —— ix35。

第二章

• 最小生成树 —— OI Wiki。
• 怎么理解拟阵（matroid） —— SleepyBag。
• 拟阵及应用 —— 好地方 bug。
• 2018 集训队论文《浅谈拟阵的一些拓展及其应用》—— 杨乾澜。