标准差为什么除以n-1

参考：https://blog.csdn.net/qian2213762498/article/details/80558018

如果要测量中国人的平均身高，假设为μ，通常会随机取假设10000人，求得均值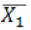

但是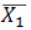，不是最准的。那么，继续抽10000人，得到。

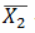如此类推，一直抽。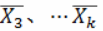

当足够幸运，出现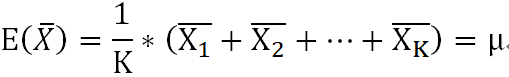，平均的平均，更接近真值。

那么称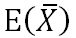为μ的无偏估计。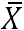的含义是指一个集合，理解为矩阵也行。

---

假设样本方差：

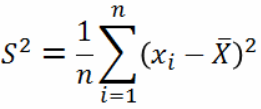，假设第k次取样，那么有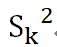和

根据无偏估计的定义，那么样本方差的无偏估计为：

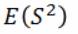，同样S² 也是代指一个集合了。以下都要以集合的思想理解，而不是单一次样本，

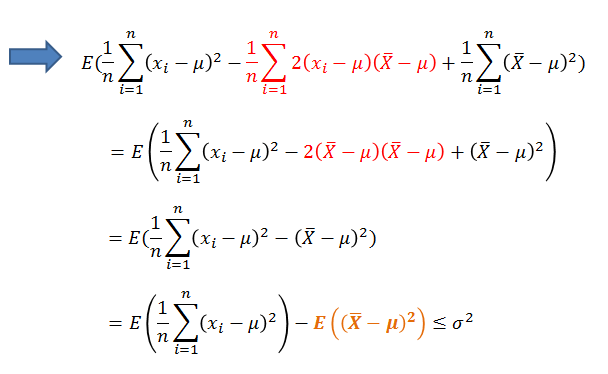
μ是已知的情况下：方差的定义：σ²  = ，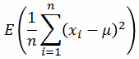

结果就是：E(S²) < σ²

 证明2：

*测绘中，常使用[ ]符号代表∑

假设观测值为l₁,l₂,l₃....l_n

算术平均值为 L = ( l₁ + l₂ + l₃ +...) / n  = [l] / n

假设未知量的真值为x，那么，真误差 Δ_i = l_i - x

Δ₁ + Δ₂ + Δ₃ + ....Δ_n = ( l₁ + l₂ + l₃ +...) - nx

也就是

[ΔΔ] =  [l] - nx

等价于

[ΔΔ] / n =  [l] /n - x

真误差 Δ_i = l_i - x

由均值算得，改正数v_i = L - l_i  （这里是证明的关键）

两式子相加：

v_i+  Δ_i = L - x

令 δ = L - x (1)

Δ_i  = -v_i + δ

那么将上式平方，然后求和

[ΔΔ] = [vv] - 2 δ [v] + nδ²

又按照正态分布，n接近无限，[v]=0;  注意，不是[vv]等于0，vv是恒为正，而v有正有负；

[ΔΔ] = [vv] +  nδ² （2）

根据（1）式子

δ = L - x  = [l] / n - x = [l-x] / n  =  [Δ] / n

δ² =  [Δ]² / n² = [  (Δ₁² +  Δ₂² + Δ₃² +..Δ_n²)  + 2Δ₁Δ₂ + 2Δ₂Δ₃ + .... + ]  / n²

δ² = [ΔΔ]  / n² +   (2Δ₁Δ₂ + 2Δ₂Δ₃ + .... + )  / n²

又因为  (2Δ₁Δ₂ + 2Δ₁Δ₃ + 2Δ₂Δ₃  .... + )  / n²   = 0 因为Δ_iΔ_j都是有正有负的。

δ² = [ΔΔ]  / n² 

将（2）代入得

[ΔΔ] = [vv] -  n（[ΔΔ]  / n² ）

[ΔΔ] = [vv]  +  [ΔΔ]  / n

所以：

[ΔΔ] -  [ΔΔ]  / n = [vv]

[ΔΔ] (n-1) / n = [vv]

[ΔΔ] /  n  =  [vv]  / (n-1)

(证毕)

又有

L = ( l₁ + l₂ + l₃ +...) / n  = [l] / n

那么根据误差传播，L的方差

m_L² =  1 / n² * m₁ ²  +  1 / n² * m₂²  + 1 / n² * m₃² +... 1 / n² * m_n² 

而因为l₁ 、 l₂、 l₃ 为等精度独立观测，因此：m₁ = m₂ = m₃ = m，m为单次观测值中误差

均值的精度： m_L²  = m² / n

而 m² = [ΔΔ] /  n 

因此：[ΔΔ] /  n  =  [vv]  / (n-1) = m²  说明了在n很大的情况下，  [vv]  / (n-1) 能算得理论上的单次观测精度，从而也能算出均值L的精度。

注：上面是理论情况，是n很大的情况下，通常来说n都是比较少的，既然理论已经有了，就按照理论上的算，所以 [vv]  / (n-1) 也只能说是“后验精度”了。