幂率定律及绘制Power-law函数
来自:Eastmount
在我们日常生活中Power Law(幂次分布,Power-law Distributions)是常见的一个数学模型,如二八原则。这个世界上是20%的人掌握80%的人的金钱去经营,20%的人口拥有80%的财富,20%的上市公司创造80%的价值,80%的收入来自20%的商品等。
下图表示人类的财富幂律分布图,极少数人拥有微弱优势的人却拥有天文级别的财富。

为什么会有这样的差别呢?
这是因为时间的乘积效应,智力上的微弱优势,乘以时间,就会得到价值(财富)几何级的增长。
经济学财富分布满足Pareto Power law
tail分布,语言中有词频的幂律分布,城市规模和数量满足幂律分布,音乐中有f分之1噪音(幂律分布)。通常人们理解幂律分布就是所谓的马太效应,二八原则,即少数人聚集了大量的财富,而大多数人的财富数量都很小,因为胜者通吃的原则。
f(x)表示某一数量指标x的发生次数,即幂率分布公式。
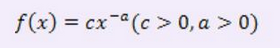

再如钱学森通信反应间隔分布:

幂率定律及绘制Power-law函数的更多相关文章
- 帕金森定律(Parkinson's Law)
帕金森定律(Parkinson's Law)是官僚主义或官僚主义现象的一种别称, 是由英国历史学家.政治学家西里尔·诺斯古德·帕金森(Cyril Northcote Parkinson)通过长期调查研 ...
- Newman的 power law 参数估计的程序matlab(转载)
转自:http://blog.sciencenet.cn/blog-4716-46173.html 对于幂率分布的估计问题是个很复杂的问题(..., the empirical detection a ...
- 封装 用canvas绘制直线的函数--面向对象
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- 康威定律(Conway's law)
系统是设计该系统的组织结构的映射. Conway's law 最初是Conway在1967年发表的论文<How Do Committees Invent?>,然后 Fred Brooks ...
- power law 幂定律
y=cx∧a 卖品销量排名与销量
- 幂次法则power law
幂次法则分布和高斯分布是两种广泛存在的数学分布.可以预测和统计相关数据. pig中用其处理数据倾斜,实现负载均衡. 个体的规模和其名次之间存在着幂次方的反比关系,R(x)=ax(-b次方) 其中,x为 ...
- 齐夫定律, Zipf's law,Zipfian distribution
齐夫定律(英语:Zipf's law,IPA英语发音:/ˈzɪf/)是由哈佛大学的语言学家乔治·金斯利·齐夫(George Kingsley Zipf)于1949年发表的实验定律. 它可以表述为: 在 ...
- gl 绘制多边形的函数解析 分类: OpenGL(转)
http://blog.csdn.net/zhongjling/article/details/7528091 1,所谓正反面 glFrontFace(GL_CCW); // 设置CCW方向为“正面 ...
- matlab绘制心形函数
matlab 7.0 绘制二维.三维心形函数 又到周六,下周就要迎来春节小长假了,想想都有些激动.在外漂了一整年,总于可以回家和父母团聚了,还有吃好吃的...,哎呀~想想都流口水呢.不过先 ...
随机推荐
- oracle goldengate 远程捕获和投递
很早之前,OGG只支持部署在数据库主机上,这叫本地化部署.而现在OGG支持远端部署,即OGG软件不安装在数据库主机上,而是安装在单独的机器上,负责数据抽取和投递. 这样做的好处: l 易于管理 - 在 ...
- 使用Wisdom RESTClient如何在Linux和Mac上获取测试报告和API文档?
使用Wisdom RESTClient自动化测试REST API,生成REST API文档, 需要先执行命令java -jar restclient-1.2.jar启动Wisdom RESTClien ...
- JDBC和servlet设计思路、DAO模式思路、MVC思路粗略总结
#JDBC和Servlet联合起来使用的项目思路: 说明:建库,最好一开始设置utf8字符集 step1: 在数据库中建表 如 create table t_user{ ...... } step ...
- Google's Machine Learning Crash Course #04# First Steps with TensorFlow
1.使用 TensorFlow 的建议 Which API(s) should you use? You should use the highest level of abstraction tha ...
- AirTest源码分析之运行器
from: https://blog.csdn.net/u012897401/article/details/82900562 使用:根据airtest文档说明,可以通过命令行来启动air脚本,需要传 ...
- c语言cgi笔记
直接输出接收的数据 #include <stdio.h>#include <stdlib.h>main(){int i,n;printf ("Content-type ...
- Excel vba map/dictionary
今天在调整一生成java代码的工具时,要用到在不同语言间互转数据类型的逻辑,原来的代码中根据excel记录的行号来计算,再到另外一个collection中获取,个人想着这也太土鳖了,于是搜了下,在vb ...
- 02: git分支管理
目录:GIT其他篇 01: git & github 02: git分支管理 目录: 1.1 Git常用命令 1.2 主要分支(保护分支) 1.3 特性分支:feature (开发分支合并到d ...
- GDI的 点 线 面 双缓冲 位图的绘制
1.输出文本 // 输出文本 ,,)); //设置字体颜色,但最后都要返回原来的字体格式 COLORREF clrBackColor = SetBkColor(hDC, RGB(,,)); //设置背 ...
- opencv学习之路(5)、鼠标和滑动条操作
一.鼠标事件 #include<opencv2/opencv.hpp> #include<iostream> using namespace cv; using namespa ...
