2018 蓝桥杯省赛 B 组模拟赛（五）

A模拟

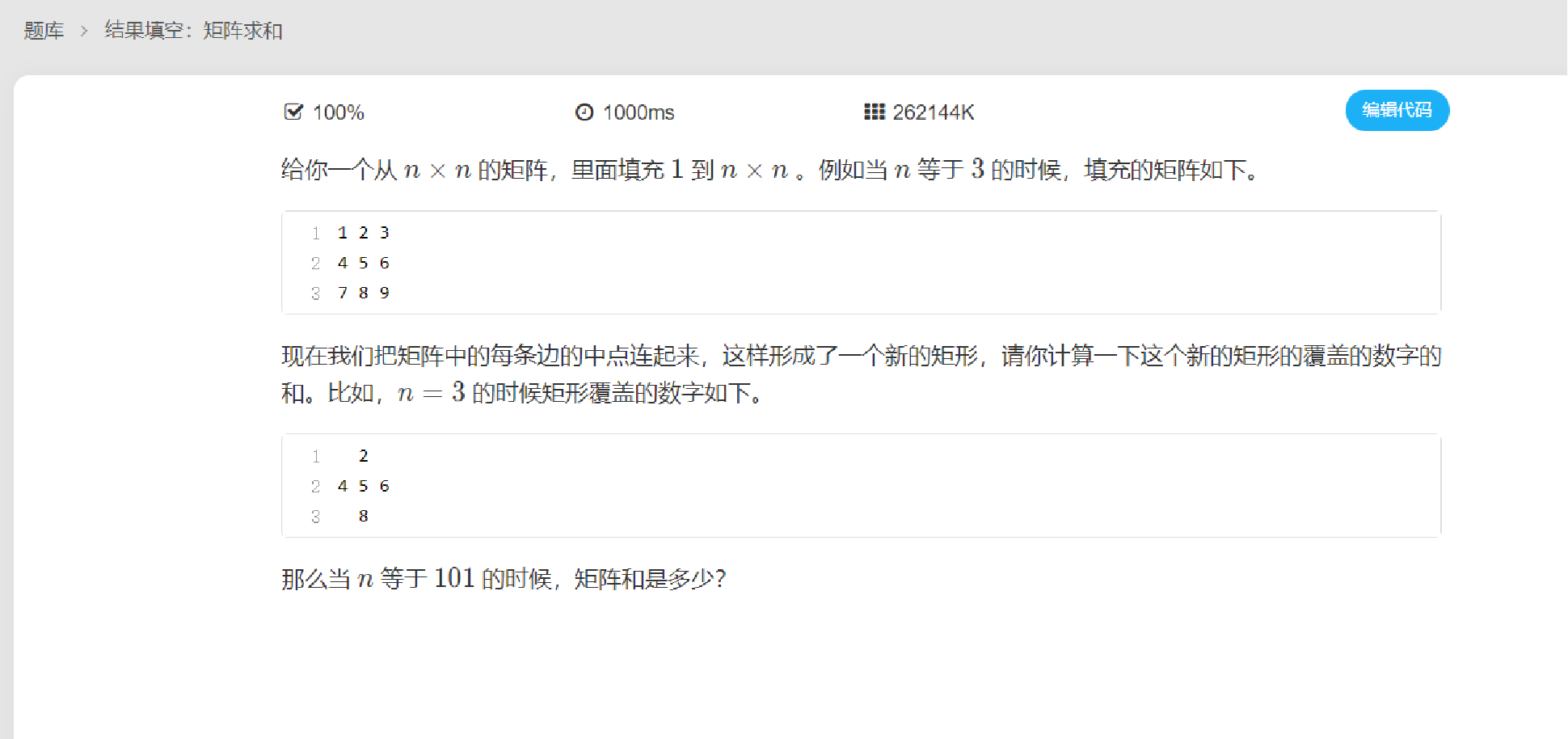
代码1

#include<bits/stdc++.h>
using namespace std;

int n = 101;
int a[120][120];
int ans = 0;

int main(){

	//填充数组
	int t = 0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			a[i][j] = ++t;
		}
	}
	int cen = n/2+1;
	int p = 1;
	int l = 1,r=n;
	//上半
	for(int i=cen;i>=1;i--){
		p = l;
		while(p<=r){
			ans += a[i][p];
			p++;
		}
		l++;
		r--;
	}
	l = 1,r = n;
	p = 1;
	cen = n/2+1+1;
	l++;
	r--;
	//下半
	for(int i=cen;i<=n;i++){
		p = l;
		while(p<=r){
			ans += a[i][p];
			p++;
		}
		l++;
		r--;
	}
	cout<<ans<<endl;
	return 0;
}

代码2

B-素数筛法打表+dfs全排列

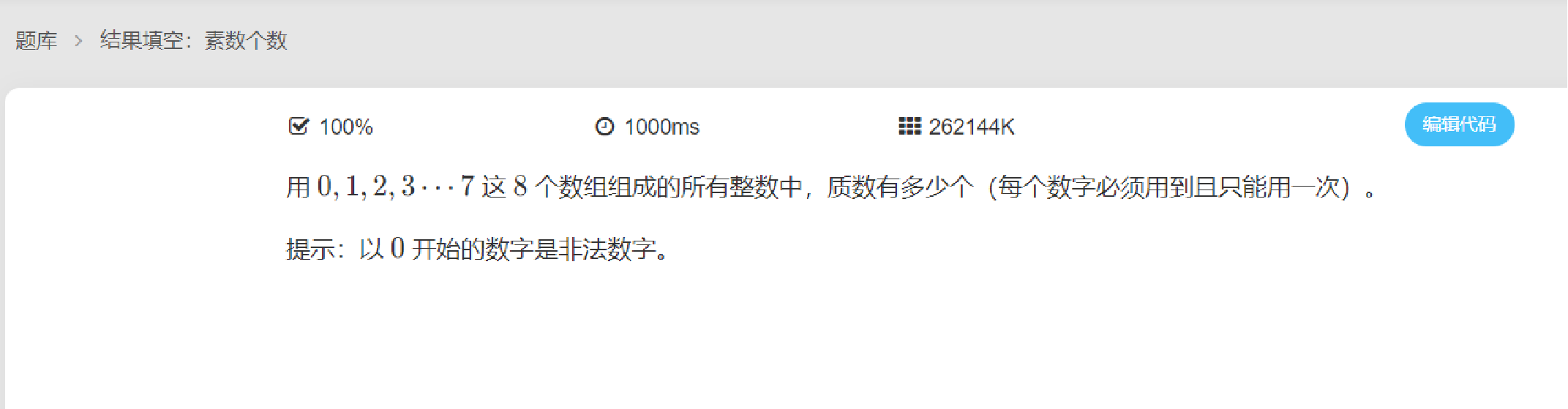
思路

因为我们需要判断一个数字是否是素数判定次数过多，所以这里使用素数筛法打表，便于查询。

然后我们需要把这 8 个数字全排列，这里和之前的全排列不太一样，这里的全排列第一个数字不能是 0 ，另外我们还需要记录我们全排列的结果。所以我们使用一个数字来记录全排列的结果 num，这样也便于查询是否是素数 。添加一个数字的时候我们通过 10*num + i 完成把先添加的数字放到数字末尾 。

这些细节处理完之后，剩下的就是一个简单的递归了。答案是2668

代码1

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

int prime[100000005];
ll ans = 0;

//素数筛打表
void Prime(){
    for (int i = 2; i <= 100000005; i++) {
        prime[i] = true;
    }
    for (int i = 1; i * i <= 100000005; i++) {
        if (prime[i]) {
            for (int j = i * i; j <= 100000005; j += i) {
                prime[j] = false;
            }
        }
    }
}

int visited[10];

//全排列
void dfs(int x,int t){
	if(x==8){
		//判断是否是素数
		if(prime[t]){
//			cout<<t<<endl;
			ans++;
		}
		return;
	}

	for(int i=0;i<=7;i++){
		if(i==0 && x==0){
			continue;
		}
		if(!visited[i]){
			visited[i] = 1;
			dfs(x+1,t*10+i);
			visited[i] = 0;
		}
	}
}

int main(){
	Prime();
	memset(visited,0,sizeof(visited));
	dfs(0,0);
	cout<<ans<<endl;
	return 0;
}

代码2

对于第一位数字不能为 0 ，我们可以通过判定 num 是否为 0 来判定第一位数字是否放 0 。

C-dfs搜索

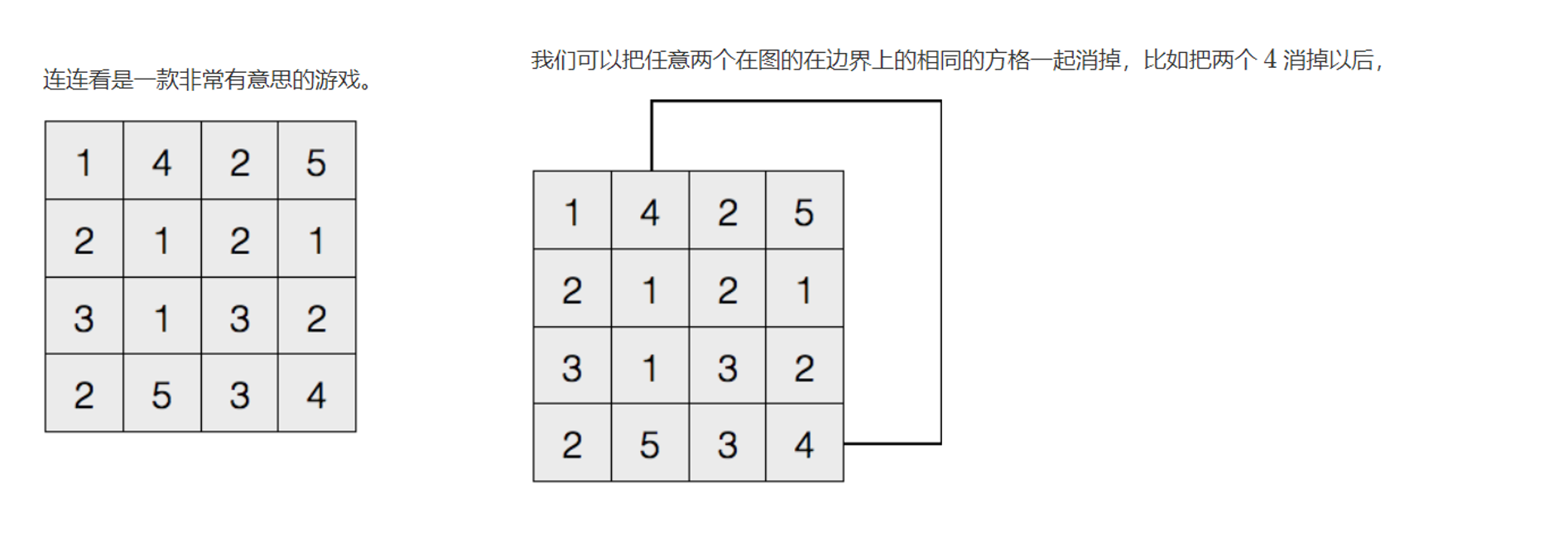
思路1：手算

思路2：dfs

1、用 dfs 求解，每一次搜索，找到两个相同的边界点，标记即可。检测边界点的方法也很简单，只需要一个点的四个方向中有一个点在地图外或者已经被标记，那么这个点就是边界点。

2、检测边界点的方法也很简单，只需要一个点的四个方向中有一个点在地图外或者已经被标记，那么这个点就是边界点。答案是 89。

代码

D-快速幂

答案：pw(x, y / 2, p) * pw(x, y / 2, p) % p

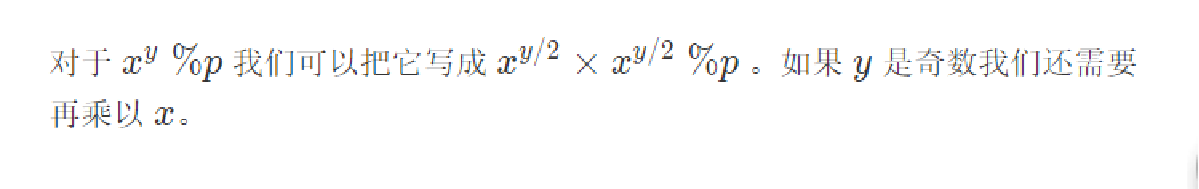
E-末尾零的个数

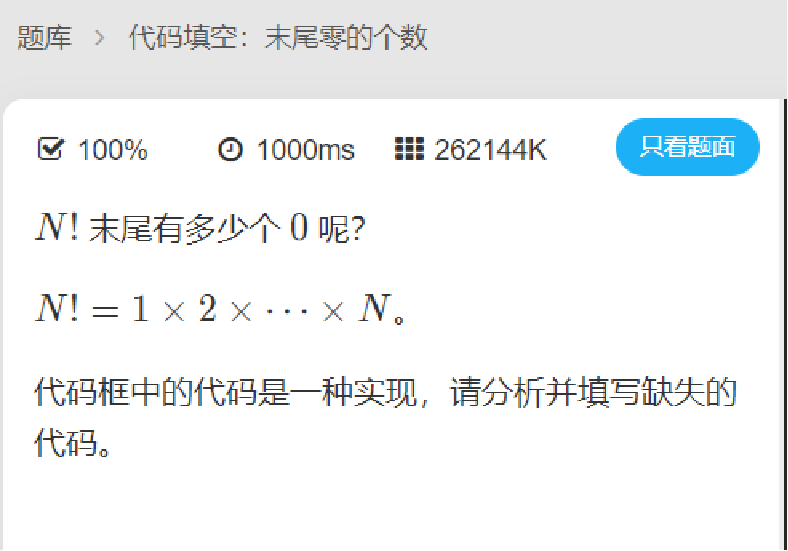
答案：n = n / 5

对于一个数的阶乘(分解成多个素数相乘)，如果想末尾出现 0 的话，只有当 5 和 2 出现的时候，才会在末尾出现 0 。

因为 2 的个数一定比 5 多。所以我们就可以得出一个结论，一个数的阶乘，末尾 0 的个数就是看里面 5 的个数。

现在变成求 1 到 n 的因子有多少个 5。对于包含 1 个 5 的数字，就是 n/5，包含两个 5 的数字个数为 n / 25。。。通过 n = n / 5 的方式，每次剥掉一层 5。

F-bfs+状态压缩

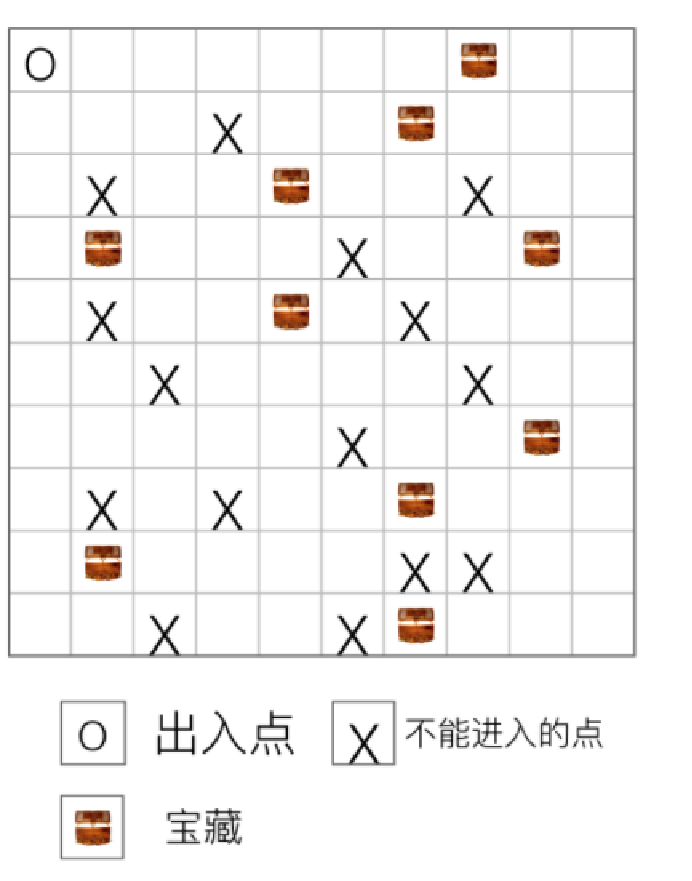
关于bfs+状态压缩：本题是典型的bfs + 状压，一个入口出口，还要拿到地图中多个东西，不知道每个东西拿的先后顺序，而且同一个点重复走的话不好标记，这时候就标记状态。

状态压缩：使用二进制标记状态

思路1

状态压缩 bfs，每个点状态用 d[x][y][state] 表示，state表示每个宝藏是否获取的状态压缩，比如(2<<10)-1 表示十进制的1023 也表示二进制的1111111111,即每个宝藏都拿到了。然后 bfs 即可。

思路2

全排列枚举选取宝藏的顺序，然后用 dfs 求出一个宝藏到另外一个宝藏之间的最短距离。优化的话，就是预处理任意两个宝藏之间的最短路距离。

思路3

手算得到答案48

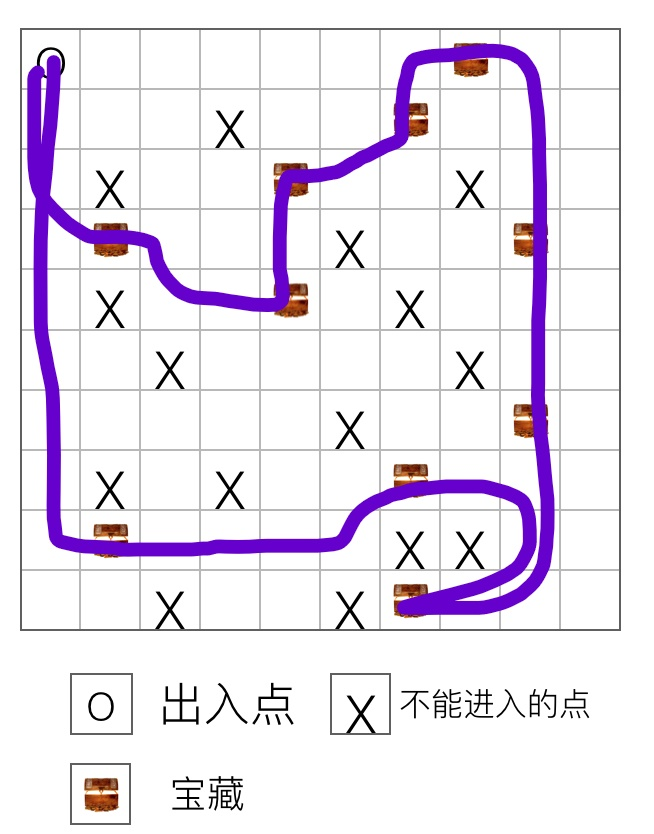
思路4

1.全排列枚举到达各个宝藏的先后顺序

2.预处理最短距离，bfs算出两两宝藏之间(包括起点/终点)相互到达的最短距离, 并作记录存入ans数组

3.通过全排列枚举的顺序，通过ans数组计算最终距离，每次排列更新最短距离

代码1

ts = s | (1 << (mat[tx][ty] - '0'));//这句话意思就是更新状态(第mat[tx][ty]个宝藏找到了，所以要把它标记为1，怎么标记呢？与s作 | 运算把s的第mat[tx][ty]为置为1)

代码4

#include <i0stream>
#include <cstdi0>
#include <cstring>
#include <alg0rithm>
#include <queue>
#include <wind0ws.h>
using namespace std;

/*
1.全排列枚举到达各个宝藏的先后顺序
2.预处理最短距离，bfs算出两两宝藏之间(包括起点/终点)相互到达的最短距离, 并作记录存入ans数组
3.通过全排列枚举的顺序，通过ans数组计算最终距离，每次排列更新最短距离
*/ 

b00l b00k[10][10];//标记地图上的是否访问过 

int bz[11][2] = {0,7,1,6,2,4,3,1,3,8,4,4,6,8,7,6,8,1,9,6,0,0};//每个宝藏的坐标
int Map[10][10]= //整个地图 2表示不能走 1表示宝藏
{
    {0,0,0,0,0,0,0,1,0,0},
    {0,0,0,2,0,0,1,0,0,0},
    {0,2,0,0,1,0,0,2,0,0},
    {0,1,0,0,0,2,0,0,1,0},
    {0,2,0,0,1,0,2,0,0,0},
    {0,0,2,0,0,0,0,2,0,0},
    {0,0,0,0,0,2,0,0,1,0},
    {0,2,0,2,0,0,1,0,0,0},
    {0,1,0,0,0,0,2,2,0,0},
    {0,0,2,0,0,2,1,0,0,0}
};
struct n0de
{
    int X,y,step;
} N0w,NeXt;

int dir[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};

int bfs(int sX,int sy, int eX, int ey)
{
    memset(b00k,0,size0f(b00k));
    N0w.X = sX;
    N0w.y = sy;
    N0w.step = 0;
    queue<n0de> q;
    q.push(N0w);//起点入队
    b00k[sX][sy] = true;
    while(!q.empty())
    {
        N0w = q.fr0nt();
        q.p0p();
        //如果到了 当前理想要到的终点 就返回步数
        if(N0w.X == eX && N0w.y == ey)
        {
            return N0w.step;
        }
        //搜寻4个方向入队
        f0r(int i = 0; i < 4; i++)
        {
            NeXt.X = N0w.X + dir[i][0];
            NeXt.y = N0w.y + dir[i][1];
            NeXt.step = N0w.step + 1;
            if(NeXt.X >= 0 && NeXt.X <= 9 && NeXt.y >= 0 && NeXt.y <= 9 && Map[NeXt.X][NeXt.y] != 2 && b00k[NeXt.X][NeXt.y] == false)
            {
                b00k[NeXt.X][NeXt.y] = true;
                q.push(NeXt);
            }
        }
    }
    return -1;
}
int main()
{
    int minn = 999999;
    int ans[11][11];//记录宝藏到宝藏(包含起点，起点当作是10号宝藏)的最短路径 

    //枚举宝藏i 到 宝藏j的最短距离 121次bfs搜索
    f0r(int i = 0; i < 11; i++)
    {
        f0r(int j = 0; j < 11; j++)
        {
            ans[i][j] = bfs(bz[i][0],bz[i][1],bz[j][0],bz[j][1]);
        }
    }

    int num[10] = {0,1,2,3,4,5,6,7,8,9};
    d0
    {
        int sum = 0;
        sum += ans[10][num[0]];//起点到第一个点的距离
        f0r(int i = 0; i < 9; i++)
        {
            sum += ans[num[i]][num[i+1]];//宝藏到宝藏每一段路的距离
        }
        sum += ans[num[9]][10];//终点回到起点的距离
        minn = min(minn,sum);//每次排列 更新最小值
    }
    while(neXt_permutati0n(num,num+10));//枚举10个宝藏到达顺序的全排列
    c0ut << minn << endl;
    return 0;
}

F-模拟，栈

思路

用栈来维护每次合并完的数，每入栈一个数以后栈顶和次栈顶比较，如果可以合并就合并为新的栈顶，并且再次与次栈顶比较直至无法合并，在合并过程中统计次数即可。

代码

#include<bits/stdc++.h>
using namespace std;

stack<int> s;
int n;
int ans = 0;

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		int d;
		scanf("%d",&d);
		while(!s.empty() && (s.top() - d) == 1){
			s.pop();//大的数 去除
			ans++;
		}
		if(!s.empty() && d - s.top() == 1){
			ans++;
		}else{
			s.push(d);//小的数保留
		}
	}
	printf("%d\n",ans);
	return 0;
}

H：找规律

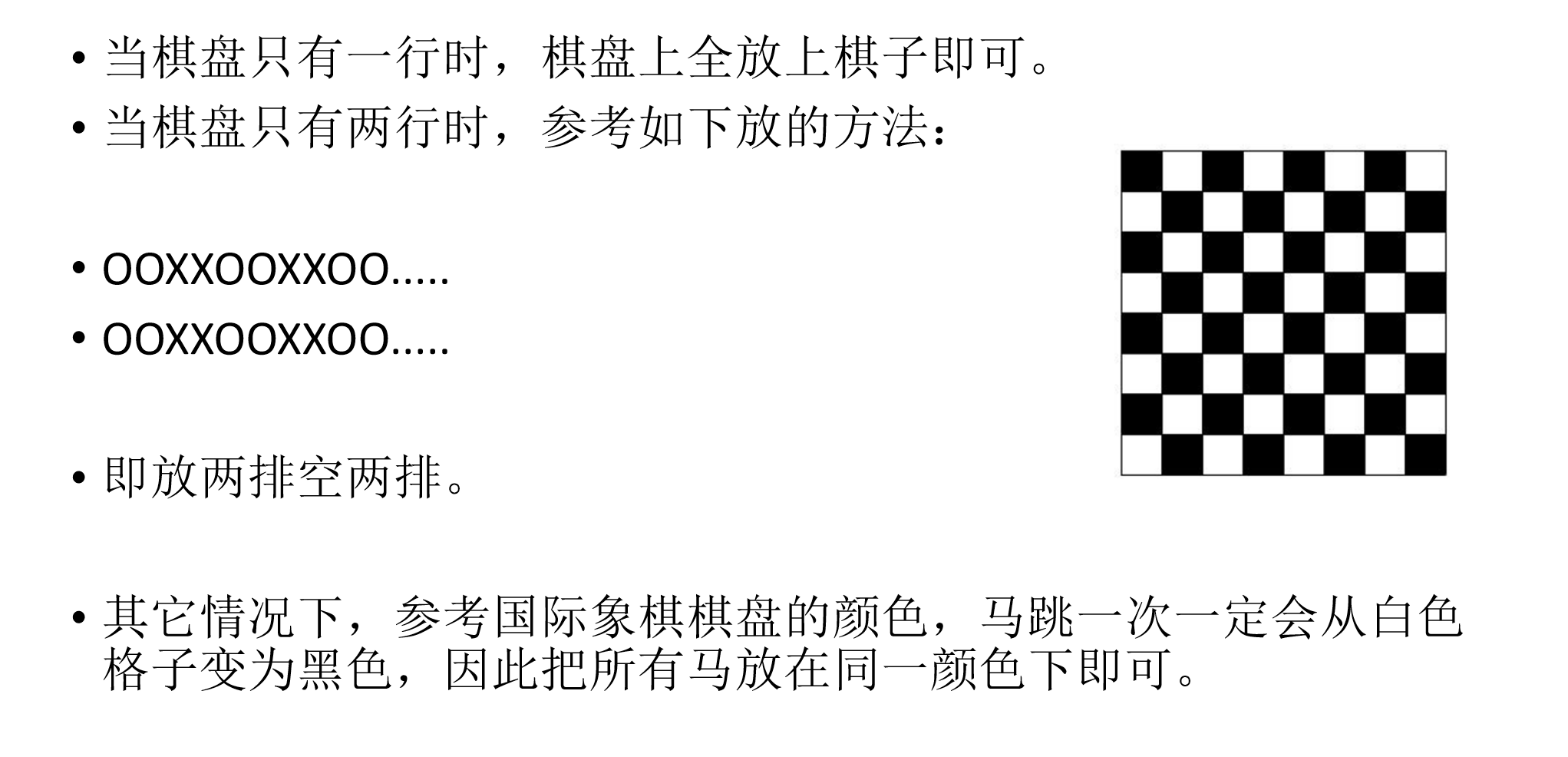
#include<bits/stdc++.h>
using namespace std;

int n,m;

int main(){
	cin>>n>>m;
	if(n > m){
		swap(n,m);
	}
	//如果只有1行，那么在列上都放上棋子
	if(n == 1){
		cout<<m<<endl;
	}else if(n == 2){
		cout<< m / 4 * 4 + min(m%4,2) * 2<<endl;
	}else{
		cout<< (n * m + 1)/2<<endl;
	}
	return 0;
}

第一眼以为是dfs暴力搜索，过3组数据，超时了。

#include<bits/stdc++.h>
using namespace std;

/*
从左到右、从上到下的顺序dfs搜索 

每个格子都有两种可能：放、不放 

dfs参数含义:横坐标、纵坐标、当前棋盘上已经放的个数
*/ 

typedef long long ll;

int n,m,ans = 0;
int a[1010][1010];
int dr[8][2] = {{-1,-2},{-2,-1},{-2,1},{1,-2},{2,-1},{-1,2},{2,1},{1,2}};

bool in(int x,int y){
	return x>=1 && x<=n && y>=1 && y<=m;
}

int valid(int x,int y){
	int flag = 1;
	for(int i=0;i<=7;i++){
		int dx = x + dr[i][0];
		int dy = y + dr[i][1];
		if(in(dx,dy) &&  (a[dx][dy] == 1)){
			flag = 0;
			break;
		}
	}
	return flag;
}

void dfs(int x,int y,int t){
	if(x==n+1){
		ans = max(ans,t);
		return;
	}
	int dx = y>=m ? x+1 : x;
	int dy = y>=m ? 1 : y+1;

	if(in(dx,dy) && a[dx][dy]!= 1 && valid(dx,dy)){
		a[dx][dy] = 1;
		dfs(dx,dy,t+1);
		a[dx][dy] = 0;
	}
	dfs(dx,dy,t);
}

int main(){
	scanf("%d%d",&n,&m);
	dfs(0,9,0);
	printf("%d\n",ans);
	return 0;
}

J-计数dp

思路1：dfs回溯+剪枝 过40%数据

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

int n,k,ans = 0;

/*参数含义:第x个数(不多于k个数)，当前剩余值t(初始为n)，当前选的数num(小于n的自然数)*/
void dfs(int x,int t,int num){ //第x个数
	if(t<0)return;
	if(x>k+1)return;
	if(x<=k+1){
		if(t==0){
			ans++;
			return;
		}
	}
	if(num>n)return;
	//枚举选当前num的个数
	for(int i=0;i<=(t/num+1);i++){
		if(num*i <=t ){
			dfs(x+i,t-num*i,num+1);
		}
	}
}

int main(){
	scanf("%d%d",&n,&k);
	dfs(1,n,1);
	printf("%d\n",ans);
	return 0;
}

思路2：计数dp

可设dp[n][k]表示将正整数n分解为不多于k个正整数相加的形式的方案数。根据题意，应分以下4种情况讨论：

1°n=1 或 k=1：n=1时只有"1=1"这1种分解方案；k=1时只有"n=n"这1种分解方案，故方案数=1；

2°n<k：相当于dp[n][k]，因正整数n不可能分解为超过n个正整数相加的形式；

3°n>k：根据"是否将n恰好分解为k个正整数相加的形式"（上界），进行讨论：

1°°将n恰好分解为k个正整数相加的形式：此时分解出的每个正整数t都满足t>=1，故相当于将分解出的k个数"都减去1"，即相当于dp[n-k][k]，也就是将正整数n-k分解为不多于k个正整数相加的形式的方案数；

2°°将n分解为小于k个正整数相加的形式：此时即dp[n][k-1]，也就是将正整数n分解为不多于k-1个正整数相加的形式的方案数；

故方案数=dp[n-k][k]+dp[n][k-1];

4°n=k：总体与3°相同，但将n恰好分解为k个正整数相加的形式时，只有"n=n/k+n/k+...+n/k"这1种分解方案，故方案数=1+dp[n][k-1]。

综上，可得以下结论：

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
int n,k;
ll dp[310][310];

int main(){
	cin>>n>>k;
	for(int i = 1;i<=n;i++){
		for(int j=1;j<=k;j++){
			//等于1的时候
			if(i==1 || k == 1){
				dp[i][j] = 1;
			}else if(j > i){
				dp[i][j] = dp[i][i];
			}else if(i > j){
				dp[i][j] = dp[i][j-1] + dp[i-j][j];
			}else{
				dp[i][j] = dp[i][j-1] + 1;
			}
		}
	}
	cout<<dp[n][k]<<endl;
	return 0;
}