【上下界网络流】bzoj2502: 清理雪道

模型：无源汇有上下界可行流

LJN：模板题吧

Description

       滑雪场坐落在FJ省西北部的若干座山上。

从空中鸟瞰，滑雪场可以看作一个有向无环图，每条弧代表一个斜坡（即雪道），弧的方向代表斜坡下降的方向。

你的团队负责每周定时清理雪道。你们拥有一架直升飞机，每次飞行可以从总部带一个人降落到滑雪场的某个地点，然后再飞回总部。从降落的地点出发，这个人可以顺着斜坡向下滑行，并清理他所经过的雪道。

由于每次飞行的耗费是固定的，为了最小化耗费，你想知道如何用最少的飞行次数才能完成清理雪道的任务。

Input

输入文件的第一行包含一个整数n (2 <= n <= 100) – 代表滑雪场的地点的数量。接下来的n行，描述1~n号地点出发的斜坡，第i行的第一个数为m_i (0 <= m_i < n) ，后面共有m_i个整数，由空格隔开，每个整数a_ij互不相同，代表从地点i下降到地点a_ij的斜坡。每个地点至少有一个斜坡与之相连。

Output

       输出文件的第一行是一个整数k – 直升飞机的最少飞行次数。

---

题目分析

题目的限制相当于这样额外连边：对于$(u,v)$若$u$在原图上可到达$v$，那么存在一条$(v,u)$的费用为1的边。现在求使每条边至少经过一次的（流量守恒的）可行流。

这个模型就是最小费用无源汇有上下界可行流（循环流）。参考：有上下界的网络流学习笔记。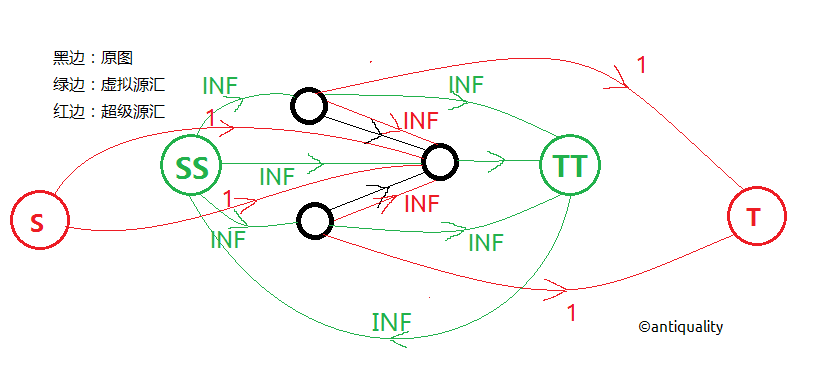

这里提供一幅简单的图供以理解。

先在原图中跑一趟最大流，将边(TT,SS)的流量作为初始答案。再在此增广的基础上，删去S,T和边(TT,SS)，并以TT为超级源、SS为超级汇跑一趟最大流。答案即是初始答案减去第二次的最大流。第二次在割去(TT,SS)之后之所以还有流量，是因为TT沿着反向弧向SS方向更新了最大流量。

可以这么说：因为整张图满足流量平衡，所以TT点流入的流量=流出的流量。而TT沿着反向弧向SS方向更新的最大流量，就是SS到TT减少最多的流量。因此两者相减就是全图的最小流。

或许这个操作叫做无源汇最小流？

 #include<bits/stdc++.h>
 const int maxn = ;
 const int maxm = ;
 const int INF = 2e9;

 struct Edge
 {
     int u,v,f,c;
     Edge(int a=, int b=, int c=, int d=):u(a),v(b),f(c),c(d) {}
 }edges[maxm];
 int n,S,T,SS,TT,ans;
 int edgeTot,head[maxn],nxt[maxm],lv[maxn];

 int read()
 {
     char ch = getchar();
     int num = , fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = -;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     return num*fl;
 }
 void addedge(int u, int v, int c)
 {
     edges[edgeTot] = Edge(u, v, , c), nxt[edgeTot] = head[u], head[u] = edgeTot++;
     edges[edgeTot] = Edge(v, u, , ), nxt[edgeTot] = head[v], head[v] = edgeTot++;
 }
 bool buildLevel()
 {
     std::queue<int> q;
     memset(lv, , sizeof lv);
     q.push(S), lv[S] = ;
     for (int tmp; q.size();)
     {
         tmp = q.front(), q.pop();
         for (int i=head[tmp]; i!=-; i=nxt[i])
         {
             int v = edges[i].v;
             if (!lv[v]&&edges[i].f < edges[i].c){
                 lv[v] = lv[tmp]+, q.push(v);
                 if (v==T) return true;
             }
         }
     }
     return false;
 }
 int fndPath(int x, int lim)
 {
     if (x==T) return lim;
     for (int i=head[x]; i!=-; i=nxt[i])
     {
         int v = edges[i].v, val;
         if (lv[x]+==lv[v]&&edges[i].f < edges[i].c){
             if ((val = fndPath(v, std::min(lim, edges[i].c-edges[i].f)))){
                 edges[i].f += val, edges[i^].f -= val;
                 return val;
             }else lv[v] = -;
         }
     }
     return ;
 }
 int dinic()
 {
     int ret = , val;
     while (buildLevel())
         while ((val = fndPath(S, INF))) ret += val;
     return ret;
 }
 int main()
 {
     memset(head, -, sizeof head);
     n = read(), S = n+, T = n+, SS = n+, TT = n+;
     for (int i=; i<=n; i++)
     {
         addedge(SS, i, INF), addedge(i, TT, INF);
         for (int k=read(); k; --k)
         {
             int x = read();
             addedge(S, x, ), addedge(i, T, );
             addedge(i, x, INF);
         }
     }
     addedge(TT, SS, INF);
     dinic();
     ans = -edges[edgeTot-].f;
     for (int i=head[S]; i!=-; i=nxt[i]) edges[i].c = edges[i^].c = edges[i].f = edges[i^].f = ;
     for (int i=head[T]; i!=-; i=nxt[i]) edges[i].c = edges[i^].c = edges[i].f = edges[i^].f = ;
     edges[edgeTot-].f = edges[edgeTot-].f = edges[edgeTot-].c = edges[edgeTot-].c = ;
     S = TT, T = SS;
     ans -= dinic();
     printf("%d\n",ans);
     return ;
 } 

END