[BZOJ3625][CF438E]小朋友和二叉树

题面

Description

我们的小朋友很喜欢计算机科学，而且尤其喜欢二叉树。

考虑一个含有\(n\)个互异正整数的序列\(c_1,c_2,\ldots,c_n\)。如果一棵带点权的有根二叉树满足其所有顶点的权值都在集合\({c_1,c_2,\ldots,c_n}\)中，我们的小朋友就会将其称作神犇的。并且他认为，一棵带点权的树的权值，是其所有顶点权值的总和。

给出一个整数\(m\)，你能对于任意的\(s(1≤s≤m)\)计算出权值为\(s\)的神犇二叉树的个数吗？请参照样例以更好的理解什么样的两棵二叉树会被视为不同的。

我们只需要知道答案关于\(998244353\)(\(7×17×223+1\),一个质数)取模后的值。

Input

第一行有\(2\)个整数\(n,m(1≤n≤10^5,1≤m≤10^5)\)。

第二行有\(n\)个用空格隔开的互异的整数\(c_1,c_2,\ldots,c_n(1≤c_i≤10^5)\)。

Output

输出\(m\)行，每行有一个整数。第\(i\)行应当含有权值恰为\(i\)的神犇二叉树的总数。请输出答案关于\(998244353\)(\(=7×17×223+1\),一个质数)取模后的结果。

Sample Input #1

2 3

1 2

Sample Output #1

1

3

9

Sample Input #2

3 10

9 4 3

Sample Output #2

0

0

1

1

0

2

4

2

6

15

Sample Input #3

5 10

13 10 6 4 15

Sample Output #3

0

0

0

1

0

1

0

2

0

5

HINT

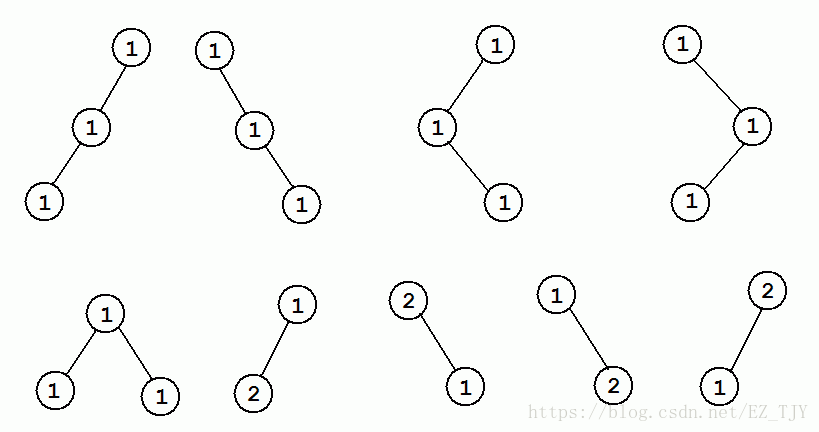
对于第一个样例，有9个权值恰好为3的神犇二叉树：

分析

设$$v_i=\sum_{k=0}^n[c_k=i]$$

也即\(k\)在\(c\)中的出现次数（在此处只能为\(1\)或\(0\)）。

设\(V(x)\)为\(v\)的生成函数：$$V(x)=\sum_{k=0}^\infty v_k x^k$$

设权值为\(i\)的神犇二叉树的个数为\(f_i\)，则我们枚举根的权值和左子树的大小，可以得到一个递归式：$$f_i=\sum_{k=0}^i v_k\sum_{j=0}^{i-k}f_j f_{i-k-j}=\sum_{x+y+z=i}v_x f_y f_z$$

当\(i=0\)时，$$f_0=1$$

那么我们发现这是一个三重卷积。我们知道数列的卷积相当于生成函数的乘法，那么我们设\(f\)的生成函数\(F(x)\)为：$$F(x)=\sum_{k=0}^\infty f_k x^k$$

则我们可以得到一个关于\(F(x)\)的一元二次方程（记得要加上\(f_0=1\)时的情况）：$$F(x)=V(x)F(x)^2+1$$

也即：$$V(x)F(x)^2-F(x)+1=0$$

那么我们使用二次方程求根公式得到：$$F(x)=\frac{1\pm\sqrt{1-4V(x)}}{2 V(x)}$$

那么到底哪个才是真的\(F(x)\)呢？

• 若\(F(x)=\displaystyle\frac{1+\sqrt{1-4V(x)}}{2V(x)}\)：

若\(x\)趋向于零，则\(F(x)\)就会趋向于\(f_0\)的值。那么我们求\(F(x)\)在\(x\to0\)下的极限：$$\lim_{x\to0}\frac{1+\sqrt{1-4V(x)}}{2V(x)}$$

因为\(v_0=0\)，所以当\(x\to0\)时\(V(x)\to0\)。则有上式相当于：$$\lim_{x\to0}\frac{1+\sqrt{1-4x}}{2x}$$

显然，由于当\(x\to0\)时有\(2x\to0\)且\(1+\sqrt{1-4x}\to2\)，则有：$$\lim_{x\to0}\frac{1+\sqrt{1-4x}}{2x}=\infty$$

舍去。

• 若\(F(x)=\displaystyle\frac{1-\sqrt{1-4V(x)}}{2V(x)}\)：

同理，有：$$\lim_{x\to0}\frac{1-\sqrt{1-4V(x)}}{2V(x)}=\lim_{x\to0}\frac{1-\sqrt{1-4x}}{2x}$$

我们发现当\(x\to0\)时\(1-\sqrt{1-4x}\to0\)且\(2x\to0\)，则我们应用洛必达法则。分子求导可得：$$\frac{d(1-\sqrt{1-4x})}{d x}=\frac{d(1-\sqrt{1-4x})}{d(1-4x)}\frac{d(1-4x)}{d x}=-\frac{1}{2\sqrt{1-4x}}\times(-4)=\frac{2}{\sqrt{1-4x}}$$

分母求导可得：$$\frac{d(2x)}{d x}=2$$

则有：$$\lim_{x\to0}\frac{1-\sqrt{1-4x}}{2x}=\frac{\lim\limits_{x\to0}\frac{2}{\sqrt{1-4x}}}{\lim\limits_{x\to0}2}=\frac{2}{2}=1$$

符合\(f_0=1\)。

综上，有$$F(x)=\frac{1-\sqrt{1-4V(x)}}{2V(x)}$$

为了方便计算，我们构造一个平方差，上下同乘\(1+\sqrt{1-4V(x)}\)：$$F(x)=\frac{\left[1-\sqrt{1-4V(x)}\right]\left[1+\sqrt{1-4V(x)}\right]}{2V(x)\left[1+\sqrt{1-4V(x)}\right]}=\frac{2}{1+\sqrt{1-4V(x)}}$$

那么我们多项式求逆+多项式求倒解决这道题。

详见https://blog.csdn.net/ez_tjy/article/details/80213166

代码

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long ll;
const ll p=998244353,g=3;
int nn,n,m,r[262145];
ll inv[262146],c[262145],gn[2][262145],ans;
inline ll pow(ll a,int b){
	ll ans=1;
	while(b){
		if(b&1)ans=ans*a%p;
		a=a*a%p;
		b>>=1;
	}
	return ans;
}
inline ll add(ll a,ll b){return a+b>p?a+b-p:a+b;}
inline ll cut(ll a,ll b){return a-b<0?a-b+p:a-b;}
void init(){
	for(n=1;n<=m;n<<=1);
	nn=n;
	gn[0][0]=gn[1][0]=1;
	gn[0][1]=pow(g,(p-1)/(n<<1));
	gn[1][1]=pow(gn[0][1],p-2);
	for(int i=2;i<(n<<1);i++){gn[0][i]=gn[0][i-1]*gn[0][1]%p;gn[1][i]=gn[1][i-1]*gn[1][1]%p;}
	inv[1]=1;
	for(int i=2;i<=(n<<1);i++)inv[i]=inv[p%i]*(p-p/i)%p;
}
void NTT(ll c[],int n,int tp=1){
	for(int i=0;i<n;i++){
		r[i]=(r[i>>1]>>1)|((i&1)*(n>>1));
		if(i<r[i])swap(c[i],c[r[i]]);
	}
	for(int i=1;i<n;i<<=1){
		for(int j=0;j<n;j+=(i<<1)){
			for(int k=0;k<i;k++){
				ll x=c[j+k],y=gn[tp!=1][nn/i*k]*c[j+k+i]%p;
				c[j+k]=add(x,y);
				c[j+k+i]=cut(x,y);
			}
		}
	}
}
void INTT(ll c[],int n){
	NTT(c,n,-1);
	for(int i=0;i<n;i++)c[i]=c[i]*inv[n]%p;
}
void inverse(ll c[],int n=n){
	static ll t[262145],tma[262145];
	t[0]=pow(c[0],p-2);
	for(int k=2;k<=n;k<<=1){
		for(int i=0;i<(k<<1);i++)tma[i]=(i<k?c[i]:0);
		for(int i=(k>>1);i<(k<<1);i++)t[i]=0;
		NTT(tma,k<<1);
		NTT(t,k<<1);
		for(int i=0;i<(k<<1);i++)t[i]=cut(add(t[i],t[i]),t[i]*t[i]%p*tma[i]%p);
		INTT(t,k<<1);
	}
	memcpy(c,t,sizeof(ll)*n);
}
void sqrt(ll c[],int n=n){
	static ll t[262145],tma[262145],tmb[262145];
	t[0]=1;
	for(int k=2;k<=n;k<<=1){
		for(int i=0;i<k;i++)tma[i]=add(t[i],t[i]);
		inverse(tma,k);
		for(int i=0;i<(k<<1);i++)tmb[i]=(i<k?c[i]:0);
		NTT(tma,k<<1);
		NTT(tmb,k<<1);
		for(int i=0;i<(k<<1);i++){
			ll tmp=tma[i];
			tma[i]=t[i];
			t[i]=tmp*tmb[i]%p;
		}
		INTT(t,k<<1);
		for(int i=0;i<(k<<1);i++)t[i]=(i<k?add(t[i],tma[i]*inv[2]%p):0);
	}
	memcpy(c,t,sizeof(ll)*n);
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		int x;
		scanf("%d",&x);
		c[x]=p-4;
	}
	c[0]=1;
	init();
	sqrt(c);
	c[0]=2;
	inverse(c);
	for(int i=1;i<=m;i++)printf("%lld\n",add(c[i],c[i]));
}