Bots(逆元，递推）

H. Bots

time limit per test

1.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Sasha and Ira are two best friends. But they aren’t just friends, they are software engineers and experts in artificial intelligence. They are developing an algorithm for two bots playing a two-player game. The game is cooperative and turn based. In each turn, one of the players makes a move (it doesn’t matter which player, it's possible that players turns do not alternate).

Algorithm for bots that Sasha and Ira are developing works by keeping track of the state the game is in. Each time either bot makes a move, the state changes. And, since the game is very dynamic, it will never go back to the state it was already in at any point in the past.

Sasha and Ira are perfectionists and want their algorithm to have an optimal winning strategy. They have noticed that in the optimal winning strategy, both bots make exactly N moves each. But, in order to find the optimal strategy, their algorithm needs to analyze all possible states of the game (they haven’t learned about alpha-beta pruning yet) and pick the best sequence of moves.

They are worried about the efficiency of their algorithm and are wondering what is the total number of states of the game that need to be analyzed?

Input

The first and only line contains integer N.

• 1 ≤ N ≤ 10⁶

Output

Output should contain a single integer – number of possible states modulo 10⁹ + 7.

Sample test(s)

Input

2

Output

19

Note

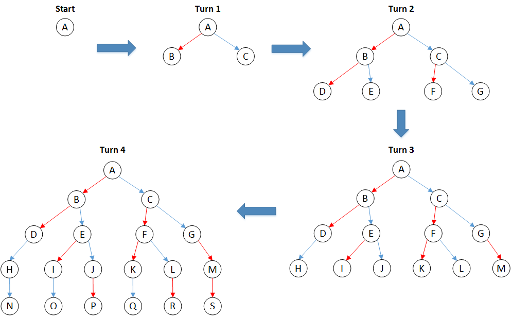
Start: Game is in state A.

• Turn 1: Either bot can make a move (first bot is red and second bot is blue), so there are two possible states after the first turn – B and C.
• Turn 2: In both states B and C, either bot can again make a turn, so the list of possible states is expanded to include D, E, F and G.
• Turn 3: Red bot already did N=2 moves when in state D, so it cannot make any more moves there. It can make moves when in state E, F and G, so states I, K and M are added to the list. Similarly, blue bot cannot make a move when in state G, but can when in D, E and F, so states H, J and L are added.
• Turn 4: Red bot already did N=2 moves when in states H, I and K, so it can only make moves when in J, L and M, so states P, R and S are added. Blue bot cannot make a move when in states J, L and M, but only when in H, I and K, so states N, O and Q are added.

Overall, there are 19 possible states of the game their algorithm needs to analyze.

#include<bits/stdc++.h>
using namespace std;
const int M = 2e6 + 10 ;
const int mod = 1e9 + 7 ;
int F[M] , Finv[M] , inv[M] ;
int n ;

void table () {
        inv[1] = 1 ;
        for (int i = 2 ; i < M ; i ++) inv[i] = (mod-mod/i) *1ll* inv[mod%i] % mod ;
        Finv[0] = F[0] = 1 ;
        for (int i = 1 ; i < M ; i ++) {
                F[i] = 1ll*F[i-1]*i%mod ;
                Finv[i] = 1ll*Finv[i-1]*inv[i]%mod ;
        }
}

int comb (int n , int m) {
        if (m < 0 || m > n) return 0 ;
        return F[n] * 1ll * Finv[n-m] % mod * Finv[m] % mod ;
}

int main () {
        table () ;
        //printf ("comb(3,3)=%d\n" , comb(3,3)) ;
        //printf ("F[3] = %d , Finv[0] = %d , Finv[3] = %d\n" , F[3] , Finv[0] , Finv[3] ) ;
        //printf ("Finv[2] = %d , inv[3] = %d\n" , Finv[2] , inv[3]) ;
        scanf ("%d" , &n) ;
        int num = 1 ;
        int sum = 1 ;
        for (int i = 1 ; i <= 2*n-1 ; i ++) {
                num = (comb(i,n) + ((num-comb(i,n))*1ll*2%mod + mod)% mod ) % mod ;
                sum = (sum+num) % mod ;
                //printf ("num = %d , comb(%d,%d)=%d\n" , num , i , n , comb(i,n)) ;
        }
        printf ("%d\n" , (1ll*sum*2+1)%mod) ;
        return 0 ;
}

首先把产生的树对半开，那么你很容易就可以发现层与层之间是存在递推关系的。

画过图你就会发现，当你从第x从画到第x+1层时，有先点扩展出了两个子节点，有些点只扩展出了一个节点。

进一步观察，你很容易想到，有些点之所以至扩展出一个节点，是因为对于这个支路它的其中一种颜色已经用完了。

而且你可以知道第x层的点数 的物理意义为，走x步的所有方案数。(一直x层共有k个点）

其中只会延伸出一个节点的点数为C（x，n） 。

所以x+1层的点数为 C(x,n) + (k-C（x，n)) * 2 ;

另外，linyujun发现了一个通式：

答案为C（2*（n+1) , n+1) - 1 ; (用眼睛看出来的，6666）