【BZOJ-4316】小C的独立集仙人掌DP + 最大独立集

4316: 小C的独立集

Time Limit: 10 Sec Memory Limit: 128 MB
Submit: 57 Solved: 41
[Submit][Status][Discuss]

Description

图论小王子小C经常虐菜，特别是在图论方面，经常把小D虐得很惨很惨。

这不，小C让小D去求一个无向图的最大独立集，通俗地讲就是：在无向图中选出若干个点，这些点互相没有边连接，并使取出的点尽量多。

小D虽然图论很弱，但是也知道无向图最大独立集是npc，但是小C很仁慈的给了一个很有特点的图：图中任何一条边属于且仅属于一个简单环，图中没有重边和自环。小C说这样就会比较水了。

小D觉得这个题目很有趣，就交给你了，相信你一定可以解出来的。

Input

第一行，两个数n， m，表示图的点数和边数。

第二~m+1行，每行两个数x，y，表示x与y之间有一条无向边。

Output

输出这个图的最大独立集。

Sample Input

5 6
1 2
2 3
3 1
3 4
4 5
3 5

Sample Output

HINT

100% n <=50000, m<=60000

Source

Solution

作为切SDOI2010Area的铺垫

仙人掌DP求最大独立集

最大独立集：感性的描述就是，一个图中，相邻点不能同时选，选出来最(多/点权总和最大)的点集

对于一般图,往往采用转化成补图求最大团

但基于树和仙人掌可以利用DP求解 (树形DP求最大独立集,详见 CodeVS1380没有上司的舞会)

至于仙人掌,就是树+基环,且强连通(描述简陋,垃圾),详见下:

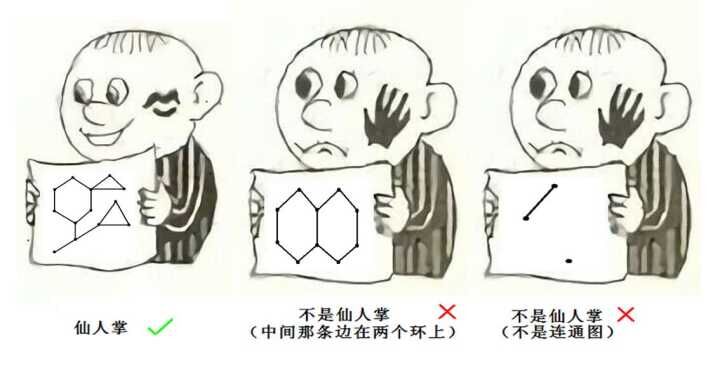
仙人掌DP的话,与树形DP同理,对于树边,可以直接进行树形DP,对于环,考虑单独处理,即单独DP,DP方式和树形DP一样

dp[x][0/1]表示 (选/不选)X节点的最优答案

转移显而易见,至于对环的考虑方法,可以采用Tarjan求强连通分量的思路,利用low和dfn进行判断更多详见某论文

Code

#include<iostream>

#include<cstring>

#include<cstdio>

#include<algorithm>

#include<cmath>

using namespace std;

int read()

{

    int x=,f=; char ch=getchar();

    while (ch<'' || ch>'') {if (ch=='-') f=-; ch=getchar();}

    while (ch>='' && ch<='') {x=x*+ch-''; ch=getchar();}

    return x*f;

}

#define maxn 100010

struct EdgeNode{int next,to;}edge[maxn<<];

int head[maxn],cnt;

void add(int u,int v) {cnt++; edge[cnt].next=head[u]; head[u]=cnt; edge[cnt].to=v;}

void insert(int u,int v) {add(u,v); add(v,u);}

int n,m,ans,tot;

int dp1[maxn][],dp2[maxn][],ring[maxn],fa[maxn],dfn[maxn],low[maxn],t,deep[maxn];

void CactusDP(int st,int tt)

{

    ring[]=st; ring[]=tt; int zz=;

    while (ring[zz]!=st) {ring[zz+]=fa[ring[zz]]; zz++;}

    dp2[][]=dp2[][]=;

    for (int i=; i<=zz; i++)

        dp2[i][]=dp2[i-][]+dp1[ring[i]][],

        dp2[i][]=max(dp2[i-][],dp2[i-][])+dp1[ring[i]][];

    int tmp=dp2[zz][];

    dp2[][]=-0x7fffffff;

    for (int i=; i<=zz; i++)

        dp2[i][]=dp2[i-][]+dp1[ring[i]][],

        dp2[i][]=max(dp2[i-][],dp2[i-][])+dp1[ring[i]][];

    dp1[st][]=tmp; dp1[st][]=dp2[zz][];

}

void TreeDP(int now)

{

    dfn[now]=low[now]=++t;

    dp1[now][]=; dp1[now][]=;

    for (int i=head[now]; i; i=edge[i].next)

        if (edge[i].to!=fa[now])

            {

                if (deep[edge[i].to]) {low[now]=min(dfn[edge[i].to],low[now]); continue;}

                fa[edge[i].to]=now;

                deep[edge[i].to]=deep[now]+;

                TreeDP(edge[i].to);

                if (low[edge[i].to]>dfn[now])

                    dp1[now][]+=dp1[edge[i].to][],dp1[now][]+=max(dp1[edge[i].to][],dp1[edge[i].to][]);

                low[now]=min(low[now],low[edge[i].to]);

            }

    for (int i=head[now]; i; i=edge[i].next)

        if (edge[i].to!=fa[now] && low[edge[i].to]==dfn[now] && deep[edge[i].to]!=deep[now]+)

            CactusDP(now,edge[i].to);

}

int main()

{

    n=read(),m=read();

    for (int u,v,i=; i<=m; i++) u=read(),v=read(),insert(u,v);

    for (int i=; i<=n; i++)

        if (!dfn[i]) {deep[i]=; fa[i]=i; TreeDP(i); ans+=max(dp1[i][],dp1[i][]);}//为了防止出现仙人掌森林的情况QAQ

    printf("%d\n",ans);

    return ;

}