python实现汉诺塔问题

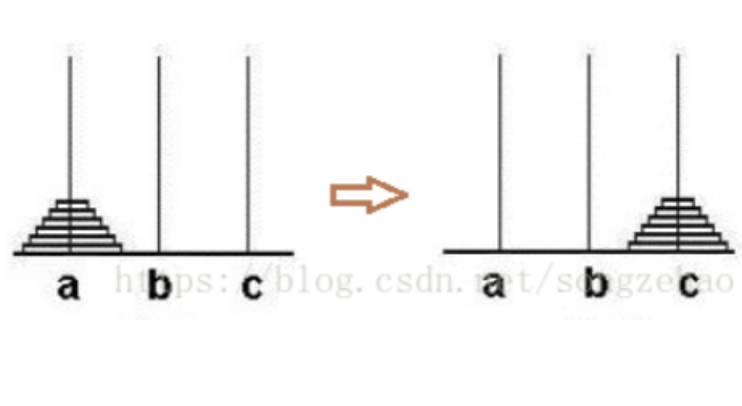
汉诺塔问题可以简单描述成为将a柱子上的圆盘按一定规则借助b柱子完美地复制到c柱子上。现假设有a，b，c三根柱子，a柱子上的圆盘从上到下依次标号为1，2，3，……，n，且为递增状态。规则：每次移动一个盘子，且只能让小的放在大的上面。目标：移动到c柱子上，与原来a上的状态相同。

算法步骤：（1）将a上的除最下面一个盘子以外的n-1的圆盘借助c柱子移动到b柱子上。
　　　　　（2）将a上剩下的圆盘（即最下面的圆盘）移动到c柱子上。
　　　　　（3）将b上的刚才一过来的n-1个圆盘再借助a柱子移动到c上去。
　　　　　（4）任务完成。

import turtle

class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return len(self.items) == 0
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
if not self.isEmpty():
return self.items[len(self.items) - 1]
def size(self):
return len(self.items)

def drawpole_3():#画出汉诺塔的poles
t = turtle.Turtle()
t.hideturtle()
def drawpole_1(k):
t.up()
t.pensize(10)
t.speed(100)
t.goto(400*(k-1), 100)
t.down()
t.goto(400*(k-1), -100)
t.goto(400*(k-1)-20, -100)
t.goto(400*(k-1)+20, -100)
drawpole_1(0)#画出汉诺塔的poles[0]
drawpole_1(1)#画出汉诺塔的poles[1]
drawpole_1(2)#画出汉诺塔的poles[2]

def creat_plates(n):#制造n个盘子
plates=[turtle.Turtle() for i in range(n)]
for i in range(n):
plates[i].up()
plates[i].hideturtle()
plates[i].shape("square")
plates[i].shapesize(1,8-i)
plates[i].goto(-400,-90+20*i)
plates[i].showturtle()
return plates

def pole_stack():#制造poles的栈
poles=[Stack() for i in range(3)]
return poles

def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
mov=poles[fp].peek()
plates[mov].goto((fp-1)*400,150)
plates[mov].goto((tp-1)*400,150)
l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
plates[mov].goto((tp-1)*400,-90+20*l)

def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
if height >= 1:
moveTower(plates,poles,height-1,fromPole,withPole,toPole)
moveDisk(plates,poles,fromPole,toPole)
poles[toPole].push(poles[fromPole].pop())
moveTower(plates,poles,height-1,withPole,toPole,fromPole)

myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
poles[0].push(i)
moveTower(plates,poles,n,0,2,1)
myscreen.exitonclick()