C++ 二分法求解方程的解

二分法是一种求解方程近似根的方法。对于一个函数 f(x)f(x)，使用二分法求 f(x)f(x) 近似解的时候，我们先设定一个迭代区间（在这个题目上，我们之后给出了的两个初值决定的区间 [-20,20][−20,20]），区间两端自变量 xx 的值对应的 f(x)f(x) 值是异号的，之后我们会计算出两端 xx 的中点位置 x'x′ 所对应的 f(x')f(x′) ，然后更新我们的迭代区间，确保对应的迭代区间的两端 xx 的值对应的 f(x)f(x) 值还会是异号的。

重复这个过程直到我们某一次中点值 x'x′ 对应的 f(x') < \epsilonf(x′)<ϵ （题目中可以直接用EPSILON）就可以将这个 x'x′ 作为近似解返回给 main 函数了。

例如：

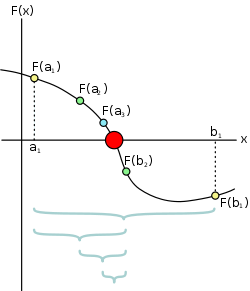
上面所示的一个迭代过程的第一次的迭代区间是 [a_1, b_1][a1​,b1​]，取中点 b_2b2​，然后第二次的迭代区间是 [a_1, b_2][a1​,b2​]，再取中点 a_2a2​，然后第三次的迭代区间是 [a_2, b_2][a2​,b2​]，然后取 a_3a3​，然后第四次的迭代区间是 [a_3, b_2][a3​,b2​]，再取红色中点 cc，我们得到发现 f(c)f(c) 的值已经小于 \epsilonϵ，输出 cc 作为近似解。

在这里，我们将用它实现对形如 px + q = 0px+q=0 的一元一次方程的求解。

在这里，你完成的程序将被输入两个正整数 pp 和 qq（你可以认为测评机给出的 0 < |p| \leq 10000<∣p∣≤1000且 0 < |q| \leq 10000<∣q∣≤1000），程序需要用二分法求出 px + q = 0px+q=0 的近似解。

输入格式

测评机会反复运行你的程序。每次程序运行时，输入为一行，包括一组被空格分隔开的符合描述的正整数 pp 和 qq。你可以认为输入数据构成的方程 px + q = 0px+q=0 都是有解且解在 [-20, 20][−20,20] 的区间内。

输出格式

输出为一行，包括一个数字。为方程 px + q = 0px+q=0 的近似解。请使用四舍五入的方式保留小数点后 44 位小数。

#include <cstdio>
#include <cmath>
#include<iostream>
#define EPSILON 1e-7
using namespace std;

double bisection(int p, int q, double(*func)(int, int, double));
double f(int p, int q, double x);
int main() {
	int p;
	int q;
	//scanf_s("%d %d", &p, &q);
	//printf_s("%.4lf\n", bisection(p, q, f));
	cin >> p >> q;
	cout << bisection(p, q, f) << endl;
	return 0;
}

double bisection(int p, int q, double(*func)(int, int, double)) {
	double m = -20.0;
	double n = 20.0;
	double  h = (m + n) / 2.0;
	double u = 0.0;
	while( abs((*func)(p, q, h))>EPSILON)
	{
		double z = (*func)(p, q, m);
		double y = (*func)(p, q, n);
	    u = (*func)(p, q, h);
		cout << u << endl;
		if (z > 0 && u > 0 || z < 0 && u < 0)
		{
			m = (m + n) / 2;
			n = n;
		}
		else
		{
			n = double(m + n) / 2;
			m = m;
		}

		h = (double)(m + n) / 2;	   

	}

	return h;

}

double f(int p, int q, double x) {
	return p * x + q;
}