python实现一般最小二乘系统辨识方法

问题：

对于一个未知参数的系统，往往需要用到系统辨识的方法，例如对于一个单输入单输出系统：

　　　　　　　　Z(k)+a₁*Z(k-1)+a₂*Z(k-2)=b₁*U(k-1)+b₂*U(k-2)+V(k)

　　　　　　　　其中：V(k)=c₁*v(k)+c₂*v(k-1)+c₃*v(k-3)

输入信号采用四阶幅值为1的M序列，高斯噪声v(k)均值为0，方差为0.1。

假设真值为a1=1.6，a2=0.7,b1=1.0,b2=0.4,c1=1.0,c2=1.6,c3=0.7。需要对以上参数进行辨识。

方法：

一般最小二乘法是系统辨识中最简单的辨识方法之一，其MATLAB实现方法十分简单，我发现网上一大把，所以我决定“翻译”一个python版的一般最小二乘辨识方法供读者参考。

本文用到的库：

import numpy as np
import matplotlib.pyplot as plt
from operator import xor
from numpy.linalg import inv

M序列的产生：

在python中，M序列的产生方法与matlab类似，先产生随机数，然后采用四阶移位寄存器滤波变换，得到我们想要的M序列。

#M序列产生
L=16
#设置M序列周期
#定义初始值
y=np.zeros(L)
u=np.zeros(L)
y1=1
y2=1
y3=1
y4=0
for i in range(0,L):
    x1=xor(y3,y4)
    x2=y1
    x3=y2
    x4=y3
    y[i]=y4
    if  y[i]>0.5:
        u[i]=-1
    else:
        u[i]=1
    y1=x1
    y2=x2
    y3=x3
    y4=x4
plt.figure(num=2)
x=np.linspace(0,15,16)
plt.bar(x,u,width=0.1)
plt.title('输入信号M序列')

高斯分布噪声：

这里采用的是random库中的函数，可以看到，我们设置的均值为0，方差为0.1。

 #产生一组16个N(0,1)的高斯分布的随机噪声
 mu=0
 sigma=0.1
 samplenum=16
 n=np.random.normal(mu,sigma,samplenum)
 plt.figure(num=1)
 plt.plot(n)
 plt.title("高斯分布随机噪声")

最小二乘辨识程序：

#最小二乘辨识过程
z=np.zeros(16)

for k in range(2,15):
    z[k]=-1.6*z[k-1]-0.7*z[k-2]+1.0*u[k-1]+0.4*u[k-2]+1.0*n[k]+1.6*n[k-1]+0.7*n[k-2] 

plt.figure(num=3)
plt.bar(x,z,width=0.1)
plt.title('输出观测值')    

H=np.array([[-z[1],-z[0],u[1],u[0]],[-z[2],-z[1],u[2],u[1]],[-z[3],-z[2],u[3],u[2]],[-z[4],-z[3],u[4],u[3]],[-z[5],-z[4],u[5],u[4]],[-z[6],-z[5],u[6],u[5]],[-z[7],-z[6],u[7],u[6]],[-z[8],-z[7],u[8],u[7]],[-z[9],-z[8],u[9],u[8]],[-z[10],-z[9],u[10],u[9]],[-z[11],-z[10],u[11],u[10]],[-z[12],-z[11],u[12],u[11]],[-z[13],-z[12],u[13],u[12]],[-z[14],-z[13],u[14],u[13]]])
Z=np.array([z[2],z[3],z[4],z[5],z[6],z[7],z[8],z[9],z[10],z[11],z[12],z[13],z[14],z[15]]) 

In_1=np.transpose(H)
In_2=np.dot(In_1,H)
In_3=inv(In_2)
In_4=np.dot(In_3,In_1)
c=np.dot(In_4,Z)

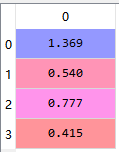
分离参数：

#分离参数并显示
a1=c[0]
a2=c[1]
b1=c[2]
b2=c[3]
print("a1的值是：",a1)
print("a2的值是：",a2)
print("b1的值是：",b1)
print("b2的值是：",b2)

注意：

由于在python中plt的库是不支持中文的，所以要加上这些代码，保证输出的图片标题的中文显示正常。

#显示中文字体
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

结果：

在网上找了半天python画针状图的资料，发现没有。。所以强行用瘦了的柱状图表示针状图了。

总结：

可以看出Python写的系统辨识误差还是有一些的，不过也是受到一般最小二乘参数辨识方法的限制，如果采用递推最小二乘，增广最小二乘等方法可能会进一步提高准确性。笔者尝试过递推最小二乘，但是与MATLAB相比，其代码量大大增加，因此在系统辨识方法上，不建议都用Python来写，MATLAB是个不错的选择。当然，喜欢写python的话，这都不是问题。

代码全文：

 # -*- coding: utf-8 -*-
 """
 Created on Wed Sep 20 16:11:27 2017
 @author: Hangingter
 """
 #一般最小二乘辨识

 #导入相应科学计算的包
 import numpy as np
 import matplotlib.pyplot as plt
 from operator import xor
 from numpy.linalg import inv

 #显示中文字体
 plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
 plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
 #产生一组16个N(0,1)的高斯分布的随机噪声
 mu=0
 sigma=0.1
 samplenum=16
 n=np.random.normal(mu,sigma,samplenum)
 plt.figure(num=1)
 plt.plot(n)
 plt.title("高斯分布随机噪声")
 #M序列产生
 L=16
 #设置M序列周期
 #定义初始值
 y=np.zeros(L)
 u=np.zeros(L)
 y1=1
 y2=1
 y3=1
 y4=0
 for i in range(0,L):
     x1=xor(y3,y4)
     x2=y1
     x3=y2
     x4=y3
     y[i]=y4
     if  y[i]>0.5:
         u[i]=-1
     else:
         u[i]=1
     y1=x1
     y2=x2
     y3=x3
     y4=x4
 plt.figure(num=2)
 x=np.linspace(0,15,16)
 plt.bar(x,u,width=0.1)
 plt.title('输入信号M序列')
 #最小二乘辨识过程
 z=np.zeros(16)

 for k in range(2,15):
     z[k]=-1.6*z[k-1]-0.7*z[k-2]+1.0*u[k-1]+0.4*u[k-2]+1.0*n[k]+1.6*n[k-1]+0.7*n[k-2] 

 plt.figure(num=3)
 plt.bar(x,z,width=0.1)
 plt.title('输出观测值')    

 H=np.array([[-z[1],-z[0],u[1],u[0]],[-z[2],-z[1],u[2],u[1]],[-z[3],-z[2],u[3],u[2]],[-z[4],-z[3],u[4],u[3]],[-z[5],-z[4],u[5],u[4]],[-z[6],-z[5],u[6],u[5]],[-z[7],-z[6],u[7],u[6]],[-z[8],-z[7],u[8],u[7]],[-z[9],-z[8],u[9],u[8]],[-z[10],-z[9],u[10],u[9]],[-z[11],-z[10],u[11],u[10]],[-z[12],-z[11],u[12],u[11]],[-z[13],-z[12],u[13],u[12]],[-z[14],-z[13],u[14],u[13]]])
 Z=np.array([z[2],z[3],z[4],z[5],z[6],z[7],z[8],z[9],z[10],z[11],z[12],z[13],z[14],z[15]]) 

 In_1=np.transpose(H)
 In_2=np.dot(In_1,H)
 In_3=inv(In_2)
 In_4=np.dot(In_3,In_1)
 c=np.dot(In_4,Z)

 #分离参数并显示
 a1=c[0]
 a2=c[1]
 b1=c[2]
 b2=c[3]
 print("a1的值是：",a1)
 print("a2的值是：",a2)
 print("b1的值是：",b1)
 print("b2的值是：",b2)

参考：

MATLAB版的系统辨识一般最小二乘方法：

http://blog.csdn.net/sinat_20265495/article/details/51426537