【bzoj3173-最长上升子序列-一题两解】

这道题不就是简单的DP吗，BZOJ在水我！不，你是错的。

·本题特点：

      不断向不同位置插入数字（按数字1,2,3,4,5,6……）,需要求出每一次插入后的最长上升子序列。

·分析

      首先我们要着眼于“数字从小到大不断插入”这个行为的特点。如图：

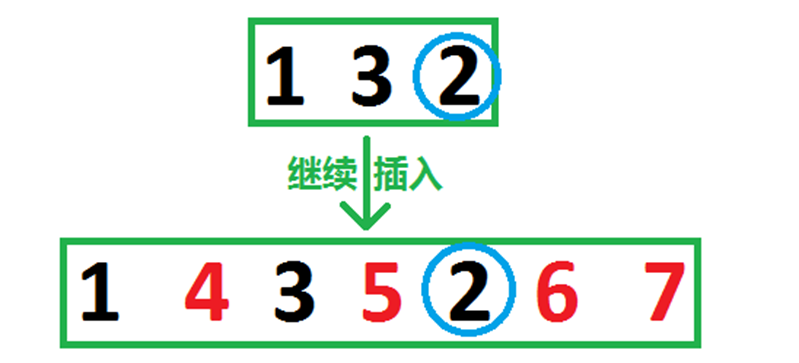
我们设f[i]表示当前插入的数是i的时候（这道题特殊，i同样表示插入了i个数），那么我们发现，如果能够快速确定最终序列长什么样子，那么就可以按照读入（插入）顺序进行一次平凡的DP。

·一切都精确地指向这个序列最终的样子是什么这一问题。也就是说呀：我们需要一种高超的技术来维护区间插入操作。然后有人将两种方法分别称为“无脑”和“奇妙”。

[1]“无脑”数据结构——Treap

      做了这题不经意间Treap就可以入门。Treap的特点是维护权值和优先级两个因素，这样的目的同时满足BST（可爱排序二叉树）和HEAP（堆）的性质，这样使得它可以维护序列的某种关键字下的排序(BST)和树的平衡(HEAP)。插入操作是Treap的基本玩法，但是插入要设法满足BST和HEAP的性质，也就是维护平衡和保证有序。维护平衡就是防止树的不当插入导致树退化成低级结构（最极端的是一条链，此时任何操作都是O(n)而不是O(logn)），维护平衡的方法就是旋转。旋转的特点是改变某些节点的父子关系以保证堆的性质，同时不会破坏维护的序列的排序（排序实际上就是树的中序遍历啦），对于一般的Treap，除了上述特点外，还会附带一个Maintain（大米饼常用Keep）函数来在旋转后维护节点信息（比如u的子树儿子节点个数等）。上述内容为Treap入门，然后使劲看代码搞懂Treap问题不大。

      对于此题，我们的美妙Treap的排序权值是当前的插入位置，与其对应地，我们用SIZE[u]标记每一个子树的节点（表示一段区间内已插入的数的个数）。最后一旦我们拿到了最终序列，就自由了，你可以尽情的用任意优化方式进行一个nlongn的DP就可以啦（例如树状数组,zkw线段树,辅助数组二分法等）。

      在数组版和指针版挣扎了一会，最终还是走上数组版Treap的道路。

大米饼习惯：ch[u][]表示左右儿子节点。一些基本操作在代码里很清晰。

 #include<stdio.h>
 #include<algorithm>
 #define go(i,a,b) for(int i=a;i<=b;i++)
 using namespace std;const int N=;
 int n,v,ch[N][],sz,P[N],siz[N],a[N],f[N],c[N],t,Re;
 void Keep(int u){siz[u]=siz[ch[u][]]+siz[ch[u][]]+;}
 void ADD(int x,int d){while(x<=n)c[x]=max(c[x],d),x+=x&-x;}
 void Get(int x){Re=;while(x)Re=max(Re,c[x]),x-=x&-x;return;}
 void Dfs(int u){if(!u)return;Dfs(ch[u][]);a[++t]=u;Dfs(ch[u][]);}
 void Rotate(int &u,int d){ch[u][d]=ch[v=ch[u][d]][d^];ch[v][d^]=u;u=v;}
 void Insert(int &u,int pos)
 {
     if(!u){siz[u=++sz]=;P[u]=rand();return;}
     int d=siz[ch[u][]]<pos;siz[u]++;
     Insert(ch[u][d],d?pos--siz[ch[u][]]:pos);
     if(P[u]<P[ch[u][d]])Rotate(u,d),Keep(ch[u][d^]),Keep(u);
 }
 int main()
 {
     scanf("%d",&n);int _=;
     go(i,,n)scanf("%d",&v),Insert(_,v);Dfs(_);
     go(i,,n)Get(a[i]),ADD(a[i],f[a[i]]=Re+);
     go(i,,n)f[i]=max(f[i],f[i-]),printf("%d\n",f[i]);
     return ;
 }//Paul_Guderian

    跑出来800ms。然后就发现了接下来的方法，400ms。

    [2]倒序构造法：对于构造最终序列，可以使用倒序的方法来反向模拟数的插入过程。可以理解我们现将所有数放进来，然后一个个拔出去。我们用一个数组表示：如果这个数还没有被拔出去，那么数组这一位为1，否则为0。如图：假设现在应该拔出a[i](即输入的：数字i插入到i位置上)

那么它在哪里？我们就在这个数组中查找第一个前缀和等于i的位置，那里就是它的真实位置（注意这里的i可以理解为第i个插入的），所以这一步我们使用二分法加一个维护前缀的东西就可以完成（偷懒就用个STL bound挺好的）。我们又一次的到了最终序列，然后就随意DP+优化就完成了。

     在代码中，大米饼出于省空间和统一化等原因，直接用树状数组维护了前缀,自认为很方便呀！

     （里面夹杂了一些读入优化输出优化）

 #include<stdio.h>
 #include<cstring>
 #include<algorithm>
 #define go(i,a,b) for(int i=a;i<=b;i++)
 #define ro(i,a,b) for(int i=a;i>=b;i--)
 using namespace std;const int N=;
 int a[N],c[N],f[N],n,l,r,M,t;
 inline void Add(int x,int d){while(x<=n)c[x]+=d,x+=x&-x;}
 inline void Up(int x,int d){while(x<=n)c[x]=max(c[x],d),x+=x&-x;}
 inline int Sum(int x){int res=;while(x)res+=c[x],x-=x&-x;return res;}
 inline int Max(int x){int M=;while(x)M=max(M,c[x]),x-=x&-x;return M;}
 inline void Nick(int x){if(x<)putchar('-'),x=-x;if(x>)Nick(x/);putchar(x%+'');}
 inline int Judy(int &x)
 {
     x=;int w=;char c=;
     while(c<''||c>''){if(c=='-')w=-;c=getchar();}
     while(c>=''&&c<='')x=x*+c-'',c=getchar();x*=w;return ;
 }
 int main()
 {
     Judy(n);go(i,,n)Judy(a[i]),Add(i,);
     ro(i,n,){l=,r=n;while(l<r)M=l+r>>,Sum(M)<a[i]+?l=M+:r=M;Add(a[i]=r,-);}
     go(i,,n)Up(a[i],f[i]=Max(a[i])+),f[i]=max(f[i],f[i-]),Nick(f[i]),puts("");
     return ;
 }//Paul_Guderian

最后一个时间效率比较：

 

 

那天我见到他们在聚会上，
他们说那真是段糟糕的日子，
那不是他们想要的生活，
也许幸福是再次寻找在路上……——————汪峰《请把我在路上叫醒》