C语言实现粒子群算法（PSO）二

上一回说了基本粒子群算法的实现，并且给出了C语言代码。这一篇主要讲解影响粒子群算法的一个重要参数---w。我们已经说过粒子群算法的核心的两个公式为：

Vid(k+1)=w*Vid(k)+c1*r1*(Pid(k)-Xid(k))+c2*r2*(Pgd(k)-Xid(k))
Xid(k+1) = Xid(k) + Vid(k+1)

标红的w即是本次我们要讨论的参数。之前w是不变的(默认取1)，而现在w是变化的，w称之为惯性权重，体现的是粒子继承先前速度的能力。

经验表明：一个较大的惯性权重有利于全局搜索，而一个较小的惯性权重则更有利于局部搜索。为了更好地平衡算法的全局搜索能力与局部搜索能力，Shi.Y提出了线性递减惯性权重(LDIW)
 即：w(k)
= w_end + (w_start- w_end)*(Tmax-k)/Tmax。其中w_start 为初始惯性权重，w_end
为迭代至最大次数时的惯性权重;k为当前迭代次数，
Tmax为最大迭代次数。一般来说，w_start=0.9,w_end=0.4时，算法的性能最好。这样随着迭代的进行，惯性权重从0.9递减到0.4,迭代初期较大的惯性权重使算法保持了较强的全局搜索能力。而迭代后期较小的惯性权重有利于算法进行更精确的局部搜索。线性惯性权重，只是一种经验做法，常用的惯性权重还包括
以下几种。
 (3) w(k) = w_start - (w_start-w_end)*(k/Tmax)^2
 (4) w(k) = w_start + (w_start-w_end)*(2*k/Tmax - (k/Tmax)^2)
 (5) w(k) = w_end*(w_start/w_end)^(1/(1+c*k/Tmax)) ,c为常数，比如取10等。
 本例的目的就是比较这5种不同的w取值，对于PSO寻优的影响。比较的方法为每种w取值，重复实验若干次(比如100次),比较平均最优解的大小，陷入次优解的次数，以及接近最优解的次数。 这样对于5种方法的优劣可以有一个直观的比较。

代码如下：

/*
 * 使用C语言实现粒子群算法(PSO) 改进版本
 * 参考自《MATLAB智能算法30个案例分析》
 * update: 16/12/3
 * 主要改进的方面体现在w的选择上面
* 本例的寻优非线性函数为
 * f(x,y) = sin(sqrt(x^2+y^2))/(sqrt(x^2+y^2)) + exp((cos(2*PI*x)+cos(2*PI*y))/2) - 2.71289
 * 该函数有很多局部极大值点，而极限位置为(0,0),在(0,0)附近取得极大值
 */
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#define c1 1.49445 //加速度因子一般是根据大量实验所得
#define c2 1.49445
#define maxgen 300  // 迭代次数
#define repeat 100 // 重复实验次数
#define sizepop 20 // 种群规模
#define popmax 2 // 个体最大取值
#define popmin -2 // 个体最小取值
#define Vmax 0.5 // 速度最大值
#define Vmin -0.5 //速度最小值
#define dim 2 // 粒子的维数
#define w_start 0.9
#define w_end 0.4
#define PI 3.1415926 //圆周率

double pop[sizepop][dim]; // 定义种群数组
double V[sizepop][dim]; // 定义种群速度数组
double fitness[sizepop]; // 定义种群的适应度数组
double result[maxgen];  //定义存放每次迭代种群最优值的数组
double pbest[sizepop][dim];  // 个体极值的位置
double gbest[dim]; //群体极值的位置
double fitnesspbest[sizepop]; //个体极值适应度的值
double fitnessgbest; // 群体极值适应度值
double genbest[maxgen][dim]; //每一代最优值取值粒子

//适应度函数
double func(double * arr)
{
    double x = *arr; //x 的值
    double y = *(arr+); //y的值
    double fitness = sin(sqrt(x*x+y*y))/(sqrt(x*x+y*y)) + exp((cos(*PI*x)+cos(*PI*y))/) - 2.71289;
    return fitness;

}
// 种群初始化
void pop_init(void)
{
    for(int i=;i<sizepop;i++)
    {
        for(int j=;j<dim;j++)
        {
            pop[i][j] = (((double)rand())/RAND_MAX-0.5)*; //-2到2之间的随机数
            V[i][j] = ((double)rand())/RAND_MAX-0.5; //-0.5到0.5之间
        }
        fitness[i] = func(pop[i]); //计算适应度函数值
    }
}
// max()函数定义
double * max(double * fit,int size)
{
    int index = ; // 初始化序号
    double max = *fit; // 初始化最大值为数组第一个元素
    static double best_fit_index[];
    for(int i=;i<size;i++)
    {
        if(*(fit+i) > max)
            max = *(fit+i);
            index = i;
    }
    best_fit_index[] = index;
    best_fit_index[] = max;
    return best_fit_index;

}
// 迭代寻优，传入的参数为一个整数，取值为1到5,分别代表5种不同的计算w的方法
void PSO_func(int n)
{
    pop_init();
    double * best_fit_index; // 用于存放群体极值和其位置(序号)
    best_fit_index = max(fitness,sizepop); //求群体极值
    int index = (int)(*best_fit_index);
    // 群体极值位置
    for(int i=;i<dim;i++)
    {
        gbest[i] = pop[index][i];
    }
    // 个体极值位置
    for(int i=;i<sizepop;i++)
    {
        for(int j=;j<dim;j++)
        {
            pbest[i][j] = pop[i][j];
        }
    }
    // 个体极值适应度值
    for(int i=;i<sizepop;i++)
    {
        fitnesspbest[i] = fitness[i];
    }
    //群体极值适应度值
    double bestfitness = *(best_fit_index+);
    fitnessgbest = bestfitness;

    //迭代寻优
    for(int i=;i<maxgen;i++)
    {
        for(int j=;j<sizepop;j++)
        {
            //速度更新及粒子更新
            for(int k=;k<dim;k++)
            {
                // 速度更新
                double rand1 = (double)rand()/RAND_MAX; //0到1之间的随机数
                double rand2 = (double)rand()/RAND_MAX;
                double w;
                double Tmax = (double)maxgen;
                switch(n)
                {
                    case :
                        w = ;
                    case :
                        w = w_end + (w_start - w_end)*(Tmax-i)/Tmax;
                    case :
                        w = w_start -(w_start-w_end)*(i/Tmax)*(i/Tmax);
                    case :
                        w = w_start + (w_start-w_end)*(*i/Tmax-(i/Tmax)*(i/Tmax));
                    case :
                        w = w_end*(pow((w_start/w_end),(/(+*i/Tmax))));
                    default:
                        w = ;
                }
                V[j][k] = w*V[j][k] + c1*rand1*(pbest[j][k]-pop[j][k]) + c2*rand2*(gbest[k]-pop[j][k]);
                if(V[j][k] > Vmax)
                    V[j][k] = Vmax;
                if(V[j][k] < Vmin)
                    V[j][k] = Vmin;
                // 粒子更新
                pop[j][k] = pop[j][k] + V[j][k];
                if(pop[j][k] > popmax)
                    pop[j][k] = popmax;
                if(pop[j][k] < popmin)
                    pop[j][k] = popmin;
            }
            fitness[j] = func(pop[j]); //新粒子的适应度值
        }
        for(int j=;j<sizepop;j++)
        {
            // 个体极值更新
            if(fitness[j] > fitnesspbest[j])
            {
                for(int k=;k<dim;k++)
                {
                    pbest[j][k] = pop[j][k];
                }
                fitnesspbest[j] = fitness[j];
            }
            // 群体极值更新
            if(fitness[j] > fitnessgbest)
            {
                for(int k=;k<dim;k++)
                    gbest[k] = pop[j][k];
                fitnessgbest = fitness[j];
            }
        }
        for(int k=;k<dim;k++)
        {
            genbest[i][k] = gbest[k]; // 每一代最优值取值粒子位置记录
        }
        result[i] = fitnessgbest; // 每代的最优值记录到数组
    }
}

// 主函数
int main(void)
{
    clock_t start,finish; //程序开始和结束时间
    start = clock(); //开始计时
    srand((unsigned)time(NULL)); // 初始化随机数种子
    for(int i=;i<=;i++)
    {
        int near_best = ; // 接近最优解的次数
        double best_sum = ; // 重复最优值求和
        double best = ; // 重复实验得到的最优解
        for(int j=;j<repeat;j++)
        {
            PSO_func(i); // 第i种w参数取值
            double * best_fit_index = max(result,maxgen);
            double best_result = *(best_fit_index+); //最优解
            if(best_result > 0.95)
                near_best++;
            if(best_result>best)
                best = best_result;
            best_sum += best_result;
        }
        double average_best = best_sum/repeat; //重复实验平均最优值
        printf("w参数的第%d种方法:\n",i);
        printf("重复实验%d次，每次实验迭代%d次,接近最优解的实验次数为%d次，求得最优值为:%lf,平均最优值为:%lf\n",repeat,maxgen,near_best,best,average_best);
    }
    finish = clock(); //结束时间
    double duration = (double)(finish - start)/CLOCKS_PER_SEC; // 程序运行时间
    printf("程序运行耗时:%lf\n",duration);
    return ;
}

程序运行结果如下：

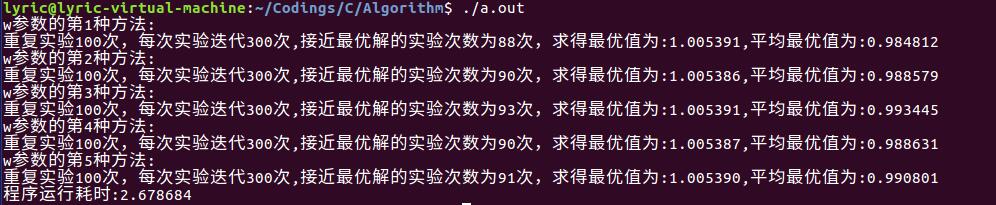
从实验的结果来看，第3种w的取法，无论是接近最优解的的次数，最优值大小，还是平均最优值，都是5种里面最好的。其原因解释如下：通过w的表达式可以看出，前期w变化较慢，取值较大，维持了算法的全局搜索能力；后期w变化变化较快，极大地提高了算法的局部搜索能力寻优能力，从而取得了很好的求解效果。

从总体上来看，在大部分的情况下，无论w是5种里面哪种取法，得到的结果都很好地接近实际的最优解，这说明了粒子群算法的搜索寻优能力还是很强的。