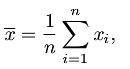R提高篇(五): 描述性统计分析

数据作为信息的载体，要分析数据中包含的主要信息,即要分析数据的主要特征（即数据的数字特征), 对于数据的数字特征, 包含数据的集中位置、分散程度和数据分布，常用统计项目如下：

• 集中趋势统计量:  均值（Mean)、中位数(Median)、众数(Mode)、百分位数
• 离散趋势统计量：标准差（sd)、方差（var)、极差（range)、变异系数(CV)、标准误、样本校正平方和（CSS）、样本未校正平方和（USS）
• 分布情况统计量：偏度、峰度
• 示例函数

集中趋势

---

• 均值(mean)：描述数据取值的平均位置，指一组数据的平均数，R 函数语法： mean(x, trim = 0, na.rm = FALSE, ...)，计算公式为：
  • • 
• 中位数(Median): 定义为数据排序位于中间位置的值, R函数语法：median(x, na.rm = FALSE)，计算公式：
  • • 
• 众数(Mode)： 就是一组数据中占比例最多的那个数， R中未提供直接调用的函数，R算法： names(table(x))[which.max(table(x))]
• 百分位数(percentile): 是中位数的推广.将数据按从小到大的排列后,对于0≤p<1,它的p分位点定义, R函数语法：quantile(x, probs = seq(0, 1, 0.25), na.rm = FALSE,names = TRUE, type = 7, ...)，计算公式为：
  • • 
    • 要计算的点到起始点的距离/终点到起始点的距离=要计算的比例
    • 实际计算中：0.75分位数与0.25分位数(第75百分位数与第25百分位数)比较重要,它们分别称为上、下四分位数,并分别记为Q3=m0.75,Q1=m0.25
• 如果一只脚放在摄氏1度的水里，另一只脚放在摄氏79度的水里，平均水温40度，你感觉舒服？ 说明只了解数据的集中趋势是不够的，还需要看数据的离散程序

离散趋势

---

• 方差（Variance): 是描述数据取值分散性的一个度量.样本方差(sample variance)是样本相对于均值的偏差平方和的平均,记为s2，R函数语法：var(x, y = NULL, na.rm = FALSE, use)，计算公式为：
  • • 
    • 其中x是样本的均值
• 标准差（Standard Deviation）: 也称均方差（mean square error），是方差的算术平方根，R函数语法：sd(x, na.rm = FALSE)，计算公式为：
  • • 
• 极差（Range): 描述样本分散性的数字特征.当数据越分散,其极差越大,R函数语法： range(..., na.rm = FALSE)，计算公式为：
  • • 
• 变异系数(CV): 又称离散系数，是刻划数据相对分散性的一种度量，它是一个无量钢的量，用百分数表示，R无对应函数，计算公式为：
  • • 
• 样本校正平方和（CSS）：无R函数，计算公式：
  • • 
• 样本未校正平方和（USS): 无R函数，计算公式：
  • • 
• 四分位差（quartile deviation）：也称为内距或四分间距（inter-quartile range），它是上四分位数（QL）与下四分位数（QU）之差，通常用Qd表示。计算公式为：
• 
• 标准误：均值标准误差就是样本均值的标准差，是描述样本均值和总体均值平均偏差程度的统计量，计算公式为：
  • • 

 分布情况统计

---

• 偏度系数：是刻划数据的对称性指标.关于均值对称的数据其偏度系数为0,右侧更分散的数据偏度系数为正,左侧更分散的数据偏度系数为负，偏度系统计算公式：
• 
• 峰度系数：当数据的总体分布为正态分布时,峰度系数近似为0;当分布较正态分布的尾部更分散时,峰度系数为正;否则为负.当峰度系数为正时,两侧极端数据较多;当峰度系数为负时,两侧极端数据较少。峰度系数计算公式：
• 

示例函数

---

• 计算各种描述性统计量函数脚本如下：

  setwd("E:\\R")
  myDescriptStat <- function(x){
    n <- length(x)                    #样本数据个数
    m <- mean(x)                      #均值
    me <- median(x)                   #中位数
    mo <- names(table(x))[which.max(table(x))]  #众数
    sd <- sd(x)                       #标准差
    v <- var(x)                       #方差
    r <- max(x) - min(x)              #极差
    cv <- 100 * sd/m                  #变异系数
    css <- sum(x - m)^2               #样本校正平方和
    uss <- sum(x^2)                   #样本未校正平方和
    R1 <- quantile(x,0.75) - quantile(x,0.25)     #四分位差
    sm <- sd/sqrt(n)                              #标准误
    g1 <- n/((n-1)*(n-2)*sd^3)*sum((x-m)^3)/sd^3  #偏度系数
    g2 <- ((n*(n+1))/((n-1)*(n-2)*(n-3))*sum((x-m)^4)/sd^4 -(3*(n-1)^2)/((n-2)*(n-3))) #峰度系数
    data.frame(N=n,Mean=m,Median=me,Mode=mo,
               Std_dev=sd,Variance=v,Range=r,
               CV=cv,CSS=css,USS=uss,
               R1=R1,SM=sm,Skewness=g1,Kurtosis=g2,
               row.names=1)
  }

• 示例结果如下：

  > setwd("E:\\R")
  > source("myDescriptStat.R")
  > w<-c(75.0,64.0,47.4,66.9,62.2,62.2,58.7,63.5,66.6,64.0,57.0,69.0,56.9,50.0,72.0)  #学生体重
  > myDescriptStat(w)
     N  Mean Median Mode  Std_dev Variance Range       CV          CSS      USS  R1       SM
  1 15 62.36   63.5 62.2 7.514823 56.47257  27.6 12.05071 2.019484e-28 59122.16 8.9 1.940319
        Skewness   Kurtosis
  1 -0.001013136 0.09653947

• 绘学生的体重的直方图和核密度估计图,并与正态分布的概率密度函数作对照图，代码及示例：

  hist(w,freq=FALSE)
  lines(density(w),col="blue")
  x<-44:76
  lines(x,dnorm(x,mean(w),sd(w)),col="red")

• 示例图形：
• 
• 结论：可以通过密度估计曲线与正态分布的概率密度曲线之间差别的大小来判断数据是否来自正态总体.从上图看,基本上可以认为学生的体重来自正态总体