培训补坑（day7:线段树的区间修改与运用）（day6是测试，测试题解以后补坑QAQ）

补坑咯~

今天围绕的是一个神奇的数据结构：线段树。（感觉叫做区间树也挺科学的。）

线段树，顾名思义就是用来查找一段区间内的最大值，最小值，区间和等等元素。

那么这个线段树有什么优势呢？

比如我们要多次查询1-n中的最大值，那么我们如果使用暴力来查找，那么我们每次查找的复杂度就是O(n)

但是如果我们把一个个区间变成树上的一个个点，并且我们严格保证树的深度，那么我们每次查找的复杂度就是O(logn)

这样就能让查询变得更快。

我们先简单讲一下线段树的存储（图中的标号就是线段树数组标号）

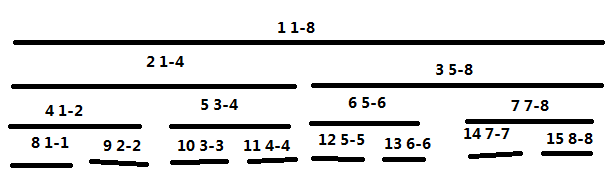
这就是线段树的存储方式。

然后我们来学习一下线段树的几个基本操作。

1：单点修改：

我们只要从1号节点往下查，如果在左边就把区间的右端点缩小，否则就把左端点增大，这个操作较为简单，不讲。

2、区间查询：

首先我们先把要查询的区间分为几段，分别刚好对应线段树上的端点，比如说2-5，我们会找到线段树中的9，5，12号节点。

然后我们在回溯的过程中合并答案就好了。

3、区间修改：

这是我们这节课的终点，但其实原理是一样的。

不过判断和区间查询略有区别。

因为区间查询的区间必须和线段树中的节点一一对应，而如果当前的区间在修改区间之内就可以进行修改。

那么区间修改有什么优化的技巧呢？

就是这个——延迟标记！

因为我们知道线段树不一定每次都查询到最底层，所以有时候如果我们把区间修改到树底，那么显然我们的时间复杂度会很高。

但是如果我们存一个延迟标记，在有需要的时候再进行传递，那么就能大大优化复杂度。

下面请看具体代码实现

void pushdown(int k,int l,int r){
    mark[ls]+=mark[k];mark[rs]+=mark[k];
    int qaq=r-l+;
    sum[ls]+=(qaq-(qaq>>))*mark[k];sum[rs]+=(qaq>>)*mark[k];mark[k]=;
}
void update(int l,int r,int a,int b,int k,int add){
    if(a<=l&&r<=b){
        mark[k]+=add;
        sum[k]+=1ll*(r-l+)*add;
        return;
    }if(mark[k]&&l!=r)pushdown(k,l,r);
    if(a<=mid)update(l,mid,a,b,ls,add);
    if(b>mid)update(mid+,r,a,b,rs,add);
    sum[k]=sum[ls]+sum[rs];
}
long long query(int l,int r,int a,int b,int k){
    if(l==a&&r==b)return sum[k];pushdown(k,l,r);
    if(b<=mid)return query(l,mid,a,b,ls);
    if(a>mid)return query(mid+,r,a,b,rs);
    return query(l,mid,a,mid,ls)+query(mid+,r,mid+,b,rs);
}

注：本模板求的是区间和。