【BZOJ4774】修路 [斯坦纳树]

修路

Time Limit: 20 Sec  Memory Limit: 256 MB

Description

　　

Input

　　

Output

　　仅一行一个整数表示答案。

Sample Input

　　5 5 2
　　1 3 4
　　3 5 2
　　2 3 1
　　3 4 4
　　2 4 3

Sample Output

　　9

HINT

　　

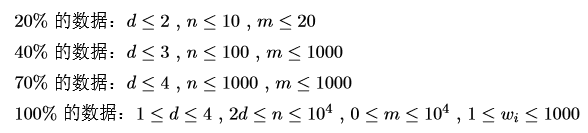
Main idea

　　给定若干对点，选择若干边，询问满足每对点都连通的最小代价。

Solution

　　发现 d 非常小，所以我们显然可以使用斯坦纳树来求解。

　　斯坦纳树是用来解决这种问题的：给定若干关键点，求使得关键点连通的最小代价。

　　我们可以令 f[i][opt] 表示以 i 为根时，关键点连通态为opt的最小代价。（以二进制表示是否连通）

　　然后我们就可以用两种方法来更新 f[i][opt]：

　　1. 设定集合x,y，x∪y=opt且x∩y=∅，那么我们显然就可以将用x,y合并来更新opt，
　　2. 若 f[j][opt] 中opt = f[i][opt]中opt，那么我们就可以以连边方式合并两个集合，这种合并方式显然可以用最短路实现，使得答案更优。

　　然后我们就可以求出所有状态的f[i][opt]，接下来再利用DP，求解。

　　定义Ans[opt]表示连通态为opt时最小代价，如果对应点同时连通或不连通则可以更新，枚举所有情况就可以求出答案了。

Code

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;

 const int ONE = ;
 const int MOD = 1e9+;

 int n,m,d;
 int x,y,z;
 int a[ONE];
 int next[ONE],first[ONE],go[ONE],w[ONE],tot;
 int All,f[ONE/][],INF;
 int q[],vis[ONE],tou,wei;
 int Ans[];

 int get()
 {
         int res=,Q=;    char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 void Add(int u,int v,int z)
 {
         next[++tot]=first[u];    first[u]=tot;    go[tot]=v;    w[tot]=z;
         next[++tot]=first[v];    first[v]=tot;    go[tot]=u;    w[tot]=z;
 }

 namespace Steiner
 {
         void pre()
         {
             memset(f,,sizeof(f));    INF=f[][];
             int num = ;
             for(int i=;i<=d;i++) f[i][<<num] = ,    num++;
             for(int i=n-d+;i<=n;i++) f[i][<<num] = , num++;
             All = (<<num) - ;
         }

         void Spfa(int opt)
         {
             while(tou<wei)
             {
                 int u=q[++tou];
                 for(int e=first[u];e;e=next[e])
                 {
                     int v=go[e];
                     if(f[v][opt] > f[u][opt] + w[e])
                     {
                         f[v][opt] = f[u][opt] + w[e];
                         if(!vis[v])
                         {
                             vis[v] = ;
                             q[++wei] = v;
                         }
                     }
                 }
                 vis[u] = ;
             }
         }

         void Deal()
         {
             for(int opt=;opt<=All;opt++)
             {
                 for(int i=;i<=n;i++)
                 {
                     for(int sub=opt;sub;sub=(sub-) & opt)
                         f[i][opt] = min(f[i][opt],f[i][sub]+f[i][opt^sub]);
                     if(f[i][opt] != INF)
                     {
                         q[++wei] = i;
                         vis[i] = ;
                     }
                 }
                 Spfa(opt);
             }
         }
 }

 bool Check(int opt)
 {
         for(int i=,j=(d<<)-; i<d; i++,j--)
         if( ((opt & (<<i))== ) !=  ((opt & (<<j))==) )
             return ;
         return ;
 }

 int main()
 {
         n=get();    m=get();    d=get();
         for(int i=;i<=m;i++)
         {
             x=get();    y=get();    z=get();
             Add(x,y,z);
         }

         Steiner::pre();
         Steiner::Deal();

         memset(Ans,,sizeof(Ans));
         for(int opt=;opt<=All;opt++)
         if(Check(opt))
         {
             for(int i=;i<=n;i++)
             Ans[opt] = min(Ans[opt], f[i][opt]);
         }

         for(int opt=;opt<=All;opt++)
         for(int sub=opt;sub;sub=(sub-) & opt)
             Ans[opt] = min(Ans[opt], Ans[sub]+Ans[opt^sub]);

         if(Ans[All] == INF) printf("-1");
         else printf("%d",Ans[All]);
 }