机器学习：评价分类结果（Precision - Recall 的平衡、P - R 曲线）

一、Precision - Recall 的平衡

　1）基础理论

• 调整阈值的大小，可以调节精准率和召回率的比重；

1. 阈值：threshold，分类边界值，score > threshold 时分类为 1，score < threshold 时分类为 0；
2. 阈值增大，精准率提高，召回率降低；阈值减小，精准率降低，召回率提高；

• 精准率和召回率是相互牵制，互相矛盾的两个变量，不能同时增高；

• 逻辑回归的决策边界不一定非是 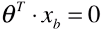，也可以是任意的值，可根据业务而定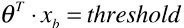：，大于 threshold 时分类为 1，小于 threshold 时分类为 0；
• 推广到其它算法，先计算出一个分数值 score ，再与 threshold 比较做分类判定；

　2）举例说明精准率和召回率相互制约的关系（一）

• 计算结果 score > 0 时，分类结果为 ★；score < 0 时，分类结果为 ●；
• ★ 类型为所关注的事件；

• 情景1：threshold = 0

• 

1. 精准率：4 / 5 = 0.80；
2. 召回率：4 / 6 = 0.67；

• 情景2：threshold  > 0；

• 

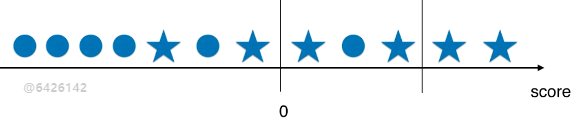
1. 精准率：2 / 2 = 1.00；
2. 召回率：2 / 6 = 0.33；

• 情景3：threshold < 0；

• 

1. 精准率：6 / 8 = 0.75；
2. 召回率：6 / 6 = 1.00；

　3）举例说明精准率和召回率相互制约的关系（二）

• LogisticRegression() 类中的 predict() 方法中，默认阈值 threshold 为 0，再根据 decision_function() 方法计算的待预测样本的 score 值进行对比分类：score < 0 分类结果为 0，score > 0 分类结果为 1；

• log_reg.decision_function(X_test)：计算所有待预测样本的 score 值，以向量的数量类型返回结果；

1. 此处的 score 值不是概率值，是另一种判断分类的方式中样本的得分，根据样本的得分对样本进行分类；

• 例

  import numpy as np
  from sklearn import datasets
  
  digits = datasets.load_digits()
  X = digits.data
  y = digits.target.copy()
  y[digits.target==9] = 1
  y[digits.target!=9] = 0
  
  from sklearn.model_selection import train_test_split
  X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
  
  from sklearn.linear_model import LogisticRegression
  log_reg = LogisticRegression()
  log_reg.fit(X_train, y_train)

1. 阈值 threshold = 0

   y_predict_1 = log_reg.predict(X_test)
   
   from sklearn.metrics import confusion_matrix
   confusion_matrix(y_test, y_predict_1)
   # 混淆矩阵：array([[403, 2],
                     [9, 36]], dtype=int64)
   
   from sklearn.metrics import precision_score
   precision_score(y_test, y_predict_1)
   # 精准率：0.9473684210526315
   
   from sklearn.metrics import recall_score
   recall_score(y_test, y_predict_1)
   # 召回率：0.8

2. 阈值 threshold = 5

   decision_score = log_reg.decision_function(X_test)
   
   # 更改 decision_score ，经过向量变化得到新的预测结果 y_predict_2；
   # decision_score > 5，增大阈值为 5；（也就是提高判断标准）
   y_predict_2 = np.array(decision_score >= 5, dtype='int')
   
   confusion_matrix(y_test, y_predict_2)
   # 混淆矩阵：array([[404,   1],
                    [ 21,  24]], dtype=int64)
   
   precision_score(y_test, y_predict_2)
   # 精准率：0.96
   
   recall_score(y_test, y_predict_2)
   # 召回率：0.5333333333333333

   # 更改阈值的思路：基于 decision_function() 方法，改变 score 值，简介更阈值，不再经过 predict() 方法，而是经过向量变化得到新的分类结果；

3. 阈值 threshold = -5

   decision_score = log_reg.decision_function(X_test)
   y_predict_3 = np.array(decision_score >= -5, dtype='int')
   
   confusion_matrix(y_test, y_predict_3)
   # 混淆矩阵：array([[390,  15],
                    [5,  40]], dtype=int64)
   
   precision_score(y_test, y_predict_3)
   # 精准率：0.7272727272727273
   
   recall_score(y_test, y_predict_3)
   # 召回率：0.8888888888888888

• 分析：

1. 精准率和召回率相互牵制，相互平衡的，一个升高，另一个就会降低；
2. 阈值越大，精准率越高，召回率越低；阈值越小，精准率越低，召回率越高；
3. 更改阈值：1）通过 LogisticRegression() 模块下的 decision_function() 方法得到预测得分；2）不使用 predict() 方法，而是重新设定阈值，通过向量转化，直接根据预测得分进行样本分类；

二、精准率 - 召回率曲线（P - R 曲线）

• 对应分类算法，都可以调用其 decision_function() 方法，得到算法对每一个样本的决策的分数值；

• LogisticRegression() 算法中，默认的决策边界阈值为 0，样本的分数值大于 0，该样本分类为 1；样本的分数值小于 0，该样本分类为 0。

• 思路：随着阈值 threshold 的变化，精准率和召回率跟着相应变化；

1. 设置不同的 threshold 值：

   decision_scores = log_reg.decision_function(X_test)
   thresholds = np.arange(np.min(decision_scores), np.max(decision_scores), 0.1)

   # 0.1 是区间取值的步长；

　1）编码实现 threshold - Precision、Recall 曲线和 P - R曲线

• import numpy as np
  import matplotlib.pyplot as plt
  from sklearn import datasets
  
  digits = datasets.load_digits()
  X = digits.data
  y = digits.target.copy()
  y[digits.target==9] = 1
  y[digits.target!=9] = 0
  
  from sklearn.model_selection import train_test_split
  X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
  
  from sklearn.linear_model import LogisticRegression
  log_reg = LogisticRegression()
  log_reg.fit(X_train, y_train)
  decision_scores = log_reg.decision_function(X_test)
  
  from sklearn.metrics import precision_score
  from sklearn.metrics import recall_score
  
  precisions = []
  recalls = []
  thresholds = np.arange(np.min(decision_scores), np.max(decision_scores), 0.1)
  
  for threshold in thresholds:
      y_predict = np.array(decision_scores >= threshold, dtype='int')
      precisions.append(precision_score(y_test, y_predict))
      recalls.append(recall_score(y_test, y_predict))

• threshold - Precision、Recall 曲线

  plt.plot(thresholds, precisions)
  plt.plot(thresholds, recalls)
  plt.show()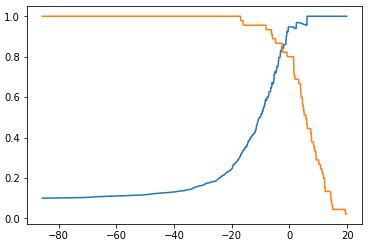

  

• P - R 曲线

  plt.plot(precisions, recalls)
  plt.show()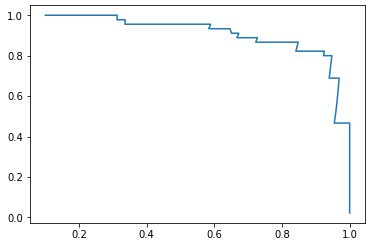

  

　2）scikit-learn 中 precision_recall_curve() 方法

• 根据 y_test、y_predicts 直接求解 precisions、recalls、thresholds；

  from sklearn.metrics import precision_recall_curve

• from sklearn.metrics import precision_recall_curve
  
  precisions, recalls, thresholds = precision_recall_curve(y_test, decision_scores)
  
  precisions.shape
  # (145,)
  
  recalls.shape
  # (145,)
  
  thresholds.shape
  # (144,)

1. 现象：thresholds 中的元素个数，比 precisions 和recalls 中的元素个数少 1 个;
2. 原因：当 precision = 1、recall = 0 时，不存在 threshold；

• threshold - Precision、Recall 曲线

  plt.plot(thresholds, precisions[:-1])
  plt.plot(thresholds, recalls[:-1])
  plt.show()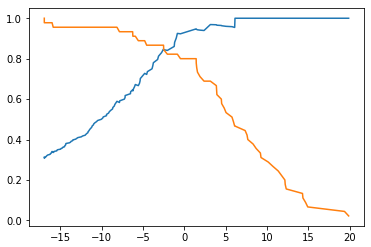

  

• P - R 曲线

  plt.plot(precisions, recalls)
  plt.show()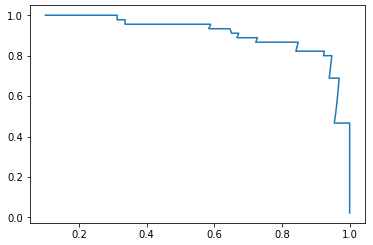

  

1. 途中曲线开始急剧下降的点，可能就是精准率和召回率平衡位置的点；

　3）分析

• 不同的模型对应的不同的 Precision - Recall 曲线：
• 

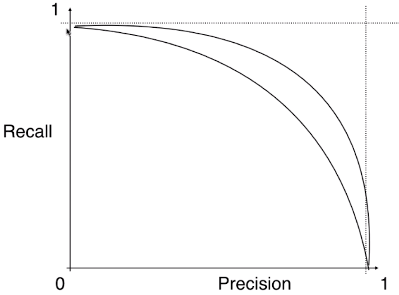
1. 外层曲线对应的模型更优；或者称与坐标轴一起包围的面积越大者越优。
2. P - R 曲线也可以作为选择算法、模型、超参数的指标；但一般不适用此曲线，而是使用 ROC 曲线；