抽样分布|t分布|中心极限定理|点估计|矩估计|最大似然法|

生物统计与实验设计-统计学基础-2&区间估计-1

正态分布参数:均值和方差

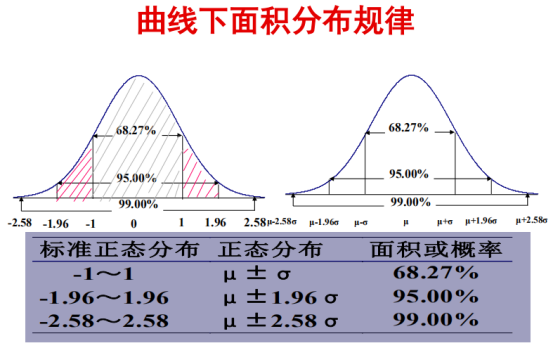
其中，选择1d是因为好算；通常，95%区分大概率事件和小概率事件，

当总体是正态分布时，可以利用常用抽样分布估计出样本参数：

抽样分布是样本估计量是样本的一个函数，在统计学中称作统计量（这就是说，统计量由样本值计算得到），因此抽样分布也是指统计量的分布。以下是当总体满足正态分布时，样本均值也满足正态分布（抽样分布是样本均值的分布，此处是正态分布）样本均值的均值与方差和总体参数之间的关系：

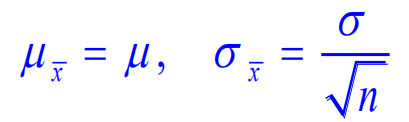
如上式，若得到一次实验的样本，样本容量就是n，计算所有样本会得到一次实验的样本均值，多次实验会得到多次实验的样本均值，假如有600次实验则会得到600个样本均值，再对这600个样本均值进行计算，计算出样本均值的均值和方差，这个样本均值的均值和方差与总体参数满足上式，根据上式关系即可估算出总体均值和总体方差。

当总体不是正态分布，可利用中心极限定理估计出总体参数：

中心极限定理：n足够大则认为样本呈正态分布，因此其样本均数也呈正态分布。

如今，为了精确计算样本均数，存在三种常见的抽样分布（抽样分布是指统计量的分布，以上例为例，就是样本均值的分布），这里的计算是为了得到右边的参数部分。

最为常用的是t分布，它的特点是对于样本含量没有要求：

化简之后是下式：

t分布的期望和方差如下：

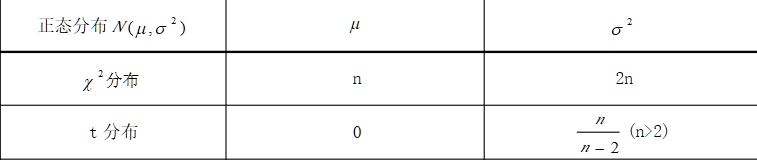
由以上期望和方差可知，t分布只与自由度有关系，与其他无关。

使用t分布作为抽样分布而不使用正态分布的理由是：对于大样本，当n足够大时，t分布和标准正态分布的曲线几乎重合；对于小样本，此时自由度为n-1，并不等同于正态分布（其实若样本容量比较小比如25，样本均值分布很大可能不是正态分布），而t分布在此时因为自由度的控制，使得曲线并非正态分布，比较符合客观事实，所以可以控制系统误差，比标准正态分布更准确。

若不使用t分布，则可以先使用特定数（比如30为界限，此处具体值依据具体问题）判断是大样本或是小样本，再选择分布：

当总体分布为正态分布，则样本指标的分布也 采用正态分布，即用Z分布来进行统计推断。

当总体分布为二项分布（n很大，P有很小）， 即当np小于等于5 时，则样本指标的分布采用泊松分布来进行统计推断。反之，当np大于等于5时，可用正态分布近似代替二项分布，则样本指标的分布采用正态分布来进行统计推断。

当小样本时：

以上是通过多个样本得到多个多个统计量再计算均值的方式，后面推出了一个样本便估计参数的方法。

目标是估计出尖值，即估计量：

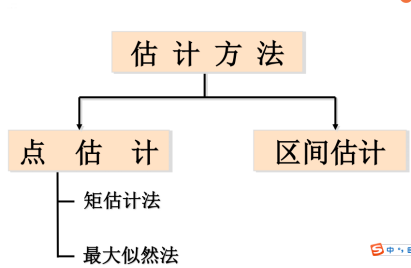
参数估计可以使用点估计和区间估计，点估计完成了参数估计的从无到有，区间估计完成了参数估计的精细化：

矩估计：提出了用原点矩的方法建立样本矩与总体矩的关系

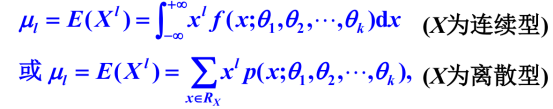
右边是总体矩左边是样本矩：eg，一阶样本矩等于参数均值。所以矩估计的思路是：将总体（含有未知参数的式子，该式子就是由之前学过的不同分布推导或者通用求积分得到）和样本（含有统计量的式子，一般就是数值一个个加或做完处理后一个个加，非常初级）联系起来的桥梁是矩估计

特点：无论总体是出于何种分布（总体矩的表达形式有所不同），最终估计出来的总体参数（仅均值和方差）的表达式完全一致。

最大似然估计是用一组样本估计出总体参数的另一种方法，它的过程是首先建立似然函数，该似然函数是在通过样本得知总体分布之后，结合样本数n，建立在n个样本同时满足某分布之上，得到它们的联合概率密度，取对数（此步骤是为了简化计算，若有其他可化简的方法皆可，它并不参与最大似然的思想）最后对似然函数求最大值（即若估计一个参数求一阶导，和估计两个参数求一阶导和二阶导）。

通过比较矩估计的和最大似然估计的参数，可以得知这一统计量和矩估计量估计出的量是不一定是一样的（但对于总体是正态分布时，估计出的参数是一样的）

经验：先最大似然，再矩估计

在通过以上方式估计参数之后，通过加入估计参数的评判标准，判断何种参数最为可靠：

无偏性：估计的参数满足抽样分布，主要看与集中趋势的比较：若估计的参数是位于所有估计的参数中的集中区域，则认为给估计的参数是无偏的，否则就是有偏的，有偏常常是系统性错误造成的。