Accelerate Framework in Swift
介绍:
最近看到这篇文章有对Accelerate框架有一个介绍,自己也按照作者给的思路整理了一遍,也算是对这一框架的一个重新的回顾和学习,在以前研究AR先关只是的时候有接触到这个框架,赞具体里面的东西没有好好的实践一下,文章中有一些关于向量和矩阵运算的实际的Swift例子。可以简单的看一下。
Introduction to the Accelerate Framework in Swift
关于这个框架和文章其实在前面介绍iOS框架系列文章的时候有提过(第一篇),对这个框架有不清楚是做什么的可以翻翻我以前总结的文章。
由于下面的运算都是些向量和矩阵的运算,要是不清楚他们的概念和运算规则的可以看下面,先了解清楚再往下看,这些具体的内容在项目当中其实还是会用到的,比如说视频编码处理、AR等等。
Accelerate
使用之前请先导入这两个框架:
NOTE: 下面所有的例子全都是在 Playground 运行验证
import UIKit
import Accelerate
import simd
1、cblas_saxpy
函数cblas_saxpy(_:_:_:_:_:_:)是一个计算常数乘以一个向量加上一个向量的函数,具体的使用看下面的例子:
var x:[Float] = [1,2,3]
var y:[Float] = [4,5,6] cblas_saxpy(3, 10, &x, 2, &y, 2)
具体的验证结果和详细的函数参数说明我们会在下面展示,大家可以先看上面给出的函数的说明推导一下结果:

2、cblas_sdot 这个函数能帮助我们计算出两个向量的数量积: ∑ a[i] * b[i]
y = [4,5,6]
/// x*y = (1*4)+(2*5)+(3*6) = 32
/// 这个函数的具体的参数可以参考上面
cblas_sdot(3, &x, 1, &y, 1)
3、sgesv_ 这个函数可以帮我们解方程,比如下面的三元三次方程,具体的验证你可以自己尝试一下,了解一下函数的参数的意义,我们已经验证过就不再重复结果。
/// 下面我们解一个三元方程
/// 7x+5y-3z = 16
/// 3x-5y+2z = -8
/// 5x+3y-7z = 0
typealias LAInt = __CLPK_integer var A:[Float] = [ 7, 3, 5, /// x
5, -5,3, /// y
-3,2,-7 /// z
] var b:[Float] = [16,-8,0] /// 定义要解的是一个几元方程
let equations = 3
/// 方程的个数
var numberOfEquations:LAInt = 3
var columnsIntA:LAInt = 3
var elementsIntB:LAInt = 3
/// 解的个数
var bSolutionCount:LAInt = 1
/// 验证是否计算有问题
var outputOk:LAInt = 0
/// [0,0,0]
var pivot = [LAInt](repeating: 0, count: equations) /// 参数定义(按顺序):求解的线性方程个数、解的个数、系数矩阵A、
/// 矩阵A的列数、排列矩阵、系数向量B、向量B的列数、输出值。
sgesv_(&numberOfEquations, &bSolutionCount, &A, &columnsIntA, &pivot, &b, &elementsIntB, &outputOk) /// outputOk == 0 说明一切计算正确
outputOk /// 这个结果就是我们想要的答案 [1, 3, 2]
b
simd + vecLib + vDSP
具体的这三个框架的内容文章中有介绍过,我们这里主要的还是验证和实践一下里面的例子,看下面的代码。
1、矩阵的加法运算,看下面的例子,注意下面的不是向量的加法,留意区别不要混淆,代码简单我直接截图顺便看验证结果:

2、vvfabsf 求绝对值的运算,代码如下:
/// fabs 求绝对值
func floats(_ n:Int32) -> [Float]{
return [Float] (repeating: 0, count: Int(n))
} var count:Int32 = 4
var aAbsoAbsolute = floats(count) var c:[Float] = [-1,-2,-3,-4]
vvfabsf(&aAbsoAbsolute, &c, &count) /// [1,2,3,4]
aAbsoAbsolute
3、vvintf 小数取整求绝对值
c = [9.987,6.576,-3.345,-4.9]
var bAbsoAbsolute = floats(count)
vvintf(&bAbsoAbsolute, &c, &count) /// [9, 6, -3, -4]
bAbsoAbsolute
4、sqrtf 开平方根
/// sqrt 开平方根 sqrtf()
c = [25,16,9,4]
var cAbsoAbsolute = floats(count)
vvsqrtf(&cAbsoAbsolute, &c, &count) /// [5, 4, 3, 2]
cAbsoAbsolute
5、分数取逆 这时候是分母和分子互换位置在做计算得来的
/// 分数取逆 这时候是分母和分子互换位置在做计算得来的
var d:[Float] = [1/3,1/5,3/9,4/2]
var dAbsoAbsolute = floats(count)
vvrecf(&dAbsoAbsolute, &d, &count) /// [3, 5, 3, 0.5]
dAbsoAbsolute
6、vDSP_vdist 这个例子其实也很有趣的,具体的例子说明可以参考最上面文章的最后一个例子,我们直接看代码和验证的结果,代码里面有比较详细的说明,还是值得一看的,能帮助我们回忆巩固一些知识点:
var points:[CGPoint] = [
CGPoint(x: 0, y: 0),
CGPoint(x: 0, y: 10),
CGPoint(x: 0, y: 20),
CGPoint(x: 0, y: 30),
CGPoint(x: 0, y: 40),
CGPoint(x: 0, y: 50),
CGPoint(x: 0, y: 60),
CGPoint(x: 0, y: 70),
CGPoint(x: 0, y: 80)
]
let path = UIBezierPath()
path.move(to: points[0])
// IMP: Remove the space between the < and points
for i in 1 ..< points.count {
path.addLine(to: points[i])
}
var xs = points.compactMap { (point) -> Float? in
return Float(point.x)
}
var ys = points.compactMap { (point) -> Float? in
return Float(point.y)
}
var distance:[Float] = [Float](repeating: 0, count: points.count)
vDSP_vdist(&xs, 1, &ys, 1, &distance,1,vDSP_Length(points.count))
/// 遍历
distance.map {$0}
/// 顺便帮忙在加深一下对 reduce 函数的理解
/// 给一个初始值 然后对集合的每一个元素进行操作
distance.reduce(0, +)
let initialResult:Float = 0
var reduceResult = distance.reduce(initialResult) { (tempResult,element) -> Float in
return tempResult + element
}
reduceResult
下面是上面例子的结果验证: 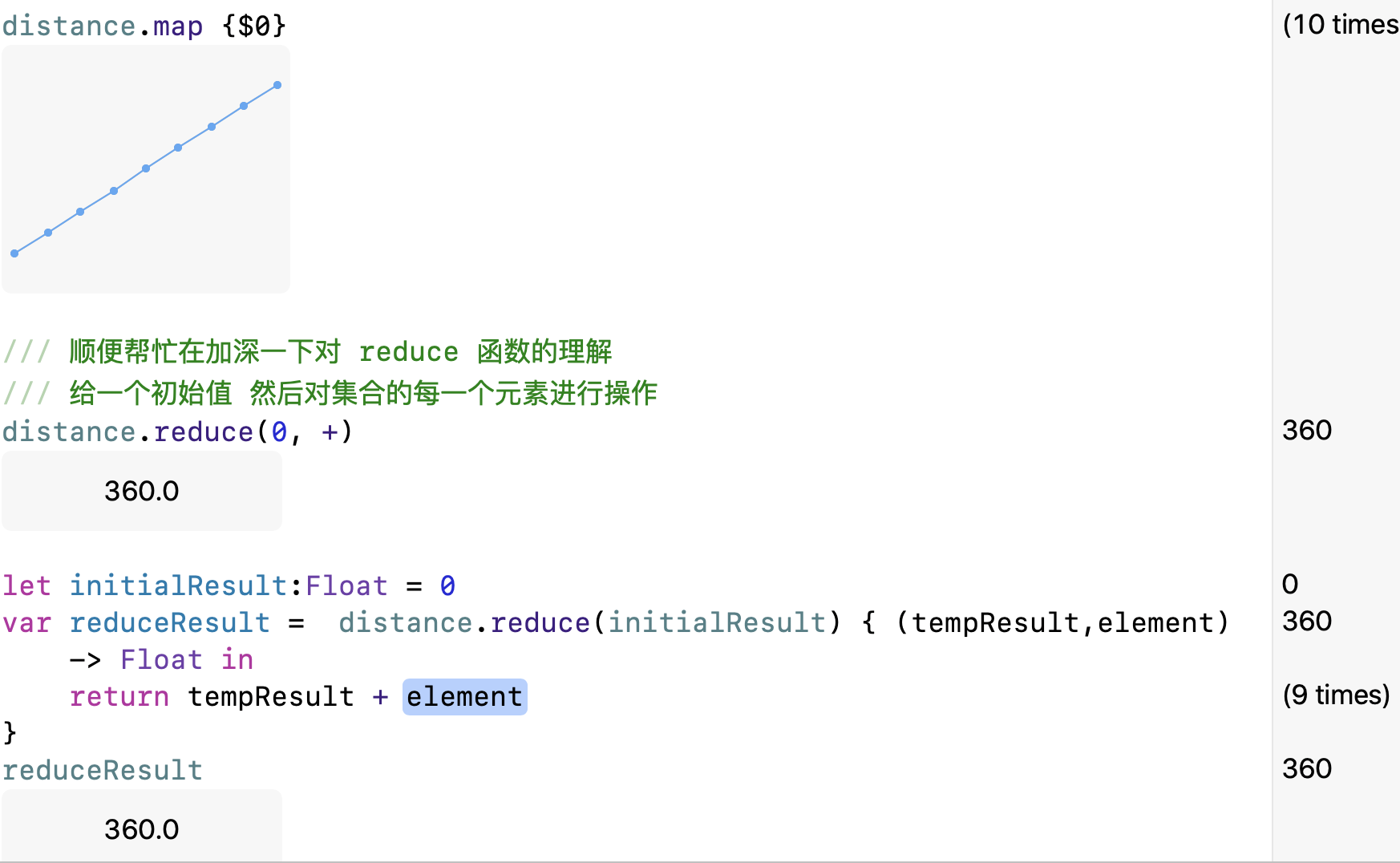
Accelerate Framework in Swift的更多相关文章
- Awesome Swift
Awesome Swift https://github.com/matteocrippa/awesome-swift A collaborative list of awesome Swift re ...
- 最新 iOS 框架整体梳理(一)
前言 这段话其实是我差不多写完文章之后再回过头来写的,原本在写文章之前想写一下写的初衷的,但当我写完之后感觉初衷没有收获更真切一些.其实到这篇为止总结出来的也就三十多个,有些是比较新的框架,有些是我们 ...
- 开发 Swift 和 Objective-C 混编的 Framework
来源:黄文臣 blog.csdn.net/hello_hwc/article/details/58320433 前言 为什么要写这样一篇文章,因为昨天和一个朋友讨论到Swift和Objective C ...
- iOS - Swift iOS 开发体系
1.iOS 开发技术体系 iOS 开发技术体系图: 层级 主要框架 Cocoa Touch UIKit 等 Media Core Graphics .OpenGl ES.Core Animation ...
- Swift 性能探索和优化分析
本文首发在 CSDN<程序员>杂志,订阅地址 http://dingyue.programmer.com.cn/. Apple 在推出 Swift 时就将其冠以先进,安全和高效的新一代编程 ...
- Swift 的 pod 第三方库
#HTTPpod 'Alamofire' #Elegant HTTP Networking in Swiftpod 'SwiftHTTP' #Thin wrapper around NSURLSess ...
- Swift开发第八篇——方法嵌套&命名空间
本篇分为两部分: 一.Swift中的方法嵌套 二.Swift中的命名空间 一.Swift中的方法嵌套 在 swift 中我们可以让方法嵌套方法,如: func appendQuery(var url: ...
- device framework(设备框架)
Table A-1 Device frameworks Name First available Prefixes Description Accelerate.framework 4.0 cbla ...
- 在同个工程中使用 Swift 和 Objective-C(Swift 2.0更新)-b
本节包含内容: Mix and Match 概述(Mix and Match Overview) 在同个应用的 target 中导入(Importing Code from Within the Sa ...
随机推荐
- AVIRIS 简介
AVIRIS 是指 机载可见光近红外成像光谱(Airborne Visible InfraRed Imaging Spectrometer).是由美国NASA下属的喷气动力实验室(JPL)开发和维护的 ...
- hexo搭建个人网站及hexo+nginx部署个人网站
先放个配置好了 server { # 监听端口 listen ; # 监听ip 换成服务器公网IP server_name mr-lin.site; location / { root /web/my ...
- Redis详解(十三)------ Redis布隆过滤器
本篇博客我们主要介绍如何用Redis实现布隆过滤器,但是在介绍布隆过滤器之前,我们首先介绍一下,为啥要使用布隆过滤器. 1.布隆过滤器使用场景 比如有如下几个需求: ①.原本有10亿个号码,现在又来了 ...
- Java IO实现文件(及文件夹)的复制 原创代码【精】
单个文件复制 FileInputStream input=new FileInputStream("C://360//fay.jpg"); FileOutputStream out ...
- Spring ( 四 )Spring的AOP动态代理、切面编程
个人博客网:https://wushaopei.github.io/ (你想要这里多有) 一.AOP切面编程 1.什么是AOP AOP是面向切面编程.全称:Aspect Oriented Pro ...
- Java实现欧拉筛与花里胡哨求质数高级大法的对比
我也不清楚这是什么高级算法,欧拉筛是昨天有位大佬,半夜无意间告诉我的 欧拉筛: 主要的含义就是我把这个数的所有倍数都弄出来,然后下次循环的时候直接就可以跳过了 import java.text.Sim ...
- Java实现 LeetCode 227 基本计算器 II(二)
227. 基本计算器 II 实现一个基本的计算器来计算一个简单的字符串表达式的值. 字符串表达式仅包含非负整数,+, - ,*,/ 四种运算符和空格 . 整数除法仅保留整数部分. 示例 1: 输入: ...
- Java实现格子取数问题
1 问题描述 有n*n个格子,每个格子里有正数或者0,从最左上角往最右下角走,只能向下和向右走,一共走两次(即从左上角往右下角走两趟),把所有经过的格子里的数加起来,求总和的最大值.如果两次经过同一个 ...
- java实现识别复制串
** 识别复制串** 代码的目标:判断一个串是否为某个基本串的简单复制构成的. 例如: abcabcabc,它由"abc"复制3次构成,则程序输出:abc aa 由"a& ...
- java实现取字母组成串
** 取字母组成串** A B C D中取5次,每个字母都可以重复取出,形成一个串. 现在要求,串中A出现的次数必须为偶数(0次也算偶数). 求可以形成多少种可能的串. 参考答案: 528 publi ...
