洛谷 P4013 数字梯形问题

->题目链接

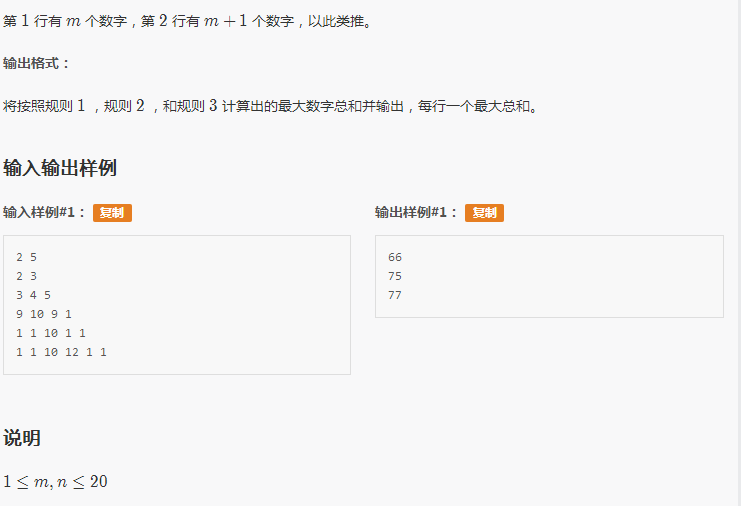
题解：

网络流。

#include<cstdio>
#include<iostream>
#include<queue>
#include<cstring>
#define N 4010
#define inf 1000000000
using namespace std;
int a[N][N],head[N],dis[N],inq[N],fa[N],n,m,num,cnt,S,T;
struct node {
    int u,v,pre,f,w;
} e[N];
void add(int u,int v,int f,int w) {
    e[++cnt].u=u;e[cnt].v=v;
    e[cnt].f=f;e[cnt].w=w;
    e[cnt].pre=head[u];head[u]=cnt;
    e[++cnt].u=v;e[cnt].v=u;
    e[cnt].f=;e[cnt].w=-w;
    e[cnt].pre=head[v];head[v]=cnt;
}
bool spfa() {
    for(int i=; i<=T; i++) dis[i]=inf;
    queue<int> q;
    q.push(S);
    inq[S]=;
    dis[S]=;
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        inq[u]=;
        for(int i=head[u]; i; i=e[i].pre)
            if(e[i].f&&dis[e[i].v]>dis[u]+e[i].w) {
                dis[e[i].v]=dis[u]+e[i].w;
                fa[e[i].v]=i;
                if(!inq[e[i].v]) {
                    inq[e[i].v]=;
                    q.push(e[i].v);
                }
            }
    }
    return dis[T]!=inf;
}
void mincost() {
    int cost=;
    while(spfa()) {
        int tmp=fa[T],x=inf;
        while(tmp) {
            int u=e[tmp].u;
            x=min(x,e[tmp].f);
            tmp=fa[e[tmp].u];
        }
        tmp=fa[T];
        while(tmp) {
            e[tmp].f-=x;
            e[tmp^].f+=x;
            tmp=fa[e[tmp].u];
        }
        cost+=x*dis[T];
    }
    printf("%d\n",-cost);
}
int hao(int i,int j) {
    return (m*+i-)*(i-)/+j;
}
void build1() {
    cnt=;
    memset(head,,sizeof(head));
    for(int i=; i<=m; i++)
        add(S,i,,-a[][i]);
    for(int i=; i<n; i++)
        for(int j=; j<=m+i-; j++)
            add(hao(i,j)+num,hao(i+,j),,-a[i+][j]),add(hao(i,j)+num,hao(i+,j+),,-a[i+][j+]);
    for(int i=; i<=m+n-; i++)
        add(hao(n,i)+num,T,,);
    for(int i=; i<=n; i++)
        for(int j=; j<=m+i-; j++)
            add(hao(i,j),hao(i,j)+num,,);

}
void build2() {
    cnt=;
    memset(head,,sizeof(head));
    for(int i=; i<=m; i++)
        add(S,i,,-a[][i]);
    for(int i=; i<=n; i++)
        for(int j=; j<=m+i-; j++)
            add(hao(i,j),hao(i+,j),,-a[i+][j]),add(hao(i,j),hao(i+,j+),,-a[i+][j+]);
    for(int i=; i<=m+n-; i++)
        add(hao(n,i),T,inf,);
}
void build3() {
    cnt=;
    memset(head,,sizeof(head));
    for(int i=; i<=m; i++)
        add(S,i,,-a[][i]);
    for(int i=; i<=n; i++)
        for(int j=; j<=m+i-; j++)
            add(hao(i,j),hao(i+,j),inf,-a[i+][j]),add(hao(i,j),hao(i+,j+),inf,-a[i+][j+]);
    for(int i=; i<=m+n-; i++)
        add(hao(n,i),T,inf,);
}
int main() {
    scanf("%d%d",&m,&n);
    num=(m*+n-)*n/;
    S=;
    T=num*+;
    for(int i=; i<=n; i++)
        for(int j=; j<=m+i-; j++)
            scanf("%d",&a[i][j]);
    build1();
    mincost();
    build2();
    mincost();
    build3();
    mincost();
    return ;
}  

AC

我走我的独木桥。