explanatory variable（independent vs dependent）、design matrix

design matrix（设计矩阵） 是统计学上的概念，一般标记为 X，是由一组对象的解释变量（explanatory variables）构成的矩阵。

1. explanatory variables

刻画的是属性列（feature column），也即一个样本、一个对象都可视为，或者抽象为，符号化为，一个多维向量，向量的每一个 component 表示一定的特征，比如身高，体重等信息，起到解释的作用和目的，也即为 explanatory variable。

命名及翻译有赖于具体的语言环境，一个独立变量（independent variable，这说的是性质上，不同的 independent variables 之间没有依赖、约束和影响关系，彼此独立，互不影响）有时也称为（这说的又是物理意义）：

• predictor variable
• regressor
• controlled variable
• manipulated variable
• explanatory variable
• feature/input variable （机器学习与模式识别中又被称为属性）

与 independent variable 相对的概念，自然是 dependent variable，同样在不同的语言环境下，它被称为：

• “response variable”,
• “regressand”,
• “predicted variable”,
• “explained variable”, （被解释，由 explanatory variables 所解释）
• “outcome variable”, “output variable” /”label”

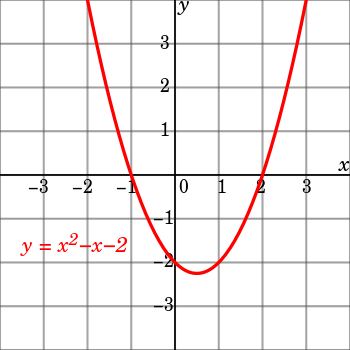
对于函数 y=x2−x−2 从变量是否独立的角度可以理解为：

• x 是 independent variable，是自变量，也即是可以自由变化的，取遍全体实数轴；
• y 是 dependent variable，是因变量，随着自变量变化而变化，不一定能取遍全体实数轴；

2. Design matrix

统计学上，由 X 所表示，每一行表示一个单个的对象，对象的各个列对应不同的属性变量，记录着属性的值。

design matrix 常用于统计模型中，比如一般的线性模型，Y=XB+U（Y 是观测值，X 是design matrix，B 是参数矩阵，U 是误差和错误）。

design matrix X 其第 i 行的第 j 列 Xij 表示的是第 i 个对象的第 j 个属性变量的值，

一个回归模型（regression model）其实是对 explanatory variables 的线性组合，因此可以通过矩阵乘法来表示：

y=Xβ

其中：

• X 是 design matrix
• β 是模型的系数（参数），每一个系数对应一个变量；
• y 样本的预测输出构成的向量；

3. example

• 单线性回归（single linear regression），比如共 7 个样本点，则模型可表示为：

  yi=β0+β1xi+ϵi
  • β0 表示截距；
  • β1 回归直线的斜率；
  ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢y1y2y3y4y5y6y7⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢1111111x1x2x3x4x5x6x7⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥[β0β1]+⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢ϵ1ϵ2ϵ3ϵ4ϵ5ϵ6ϵ7⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥