洛谷3388 【模板】割点 tarjan算法

题目描述

给出一个n个点，m条边的无向图，求图的割点。

关于割点

在无向连通图中，如果将其中一个点以及所有连接该点的边去掉，图就不再连通，那么这个点就叫做割点（cut vertex / articulation point）。

题解

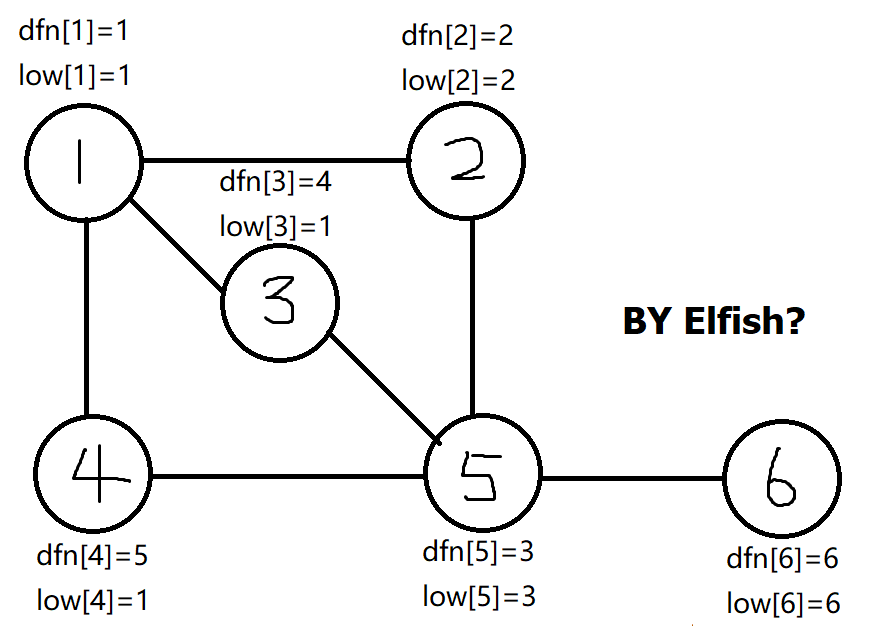
在一个无向图里的割点分为两种，第一种就是一棵树的根节点并且他的度要大于等于2，删去这个点他的子树就不连通了(如上图的1号点)。

第二种就要用到tarjan算法的思想，tarjan求出每个点的dfs顺序，然后记录他子树中能访问到的dfn最早的点。如果一个点不为根且他的子树的low大于他的dfn，即他的子树要在访问过他之后才能访问那个点，那么这个点删去以后图也会不连通。(如上图中的5，6号点必须在访问5之后才能访问到)。

代码

//洛谷3388 割点 tarjan
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m,cnt,head[];
int dfn[],low[],cut[];
struct edge{
    int next,to;
}e[];
void insert(int u,int v){
    cnt++;
    e[cnt].next=head[u];e[cnt].to=v;
    head[u]=cnt;
}
int top,ind,k;
void tarjan(int x,int root){
    dfn[x]=low[x]=++ind;
    int du=;
    for(int i=head[x];i;i=e[i].next){
        int s=e[i].to;
        if(!dfn[s]){
            tarjan(s,root);
            low[x]=min(low[s],low[x]);
            if(low[s]>=dfn[x]&&x!=root)cut[x]=;
            if(x==root)du++;
        }
        low[x]=min(dfn[s],low[x]);
    }
    if(x==root&&du>=)cut[root]=;
}
int mx=;
int ans;
int main(){
    scanf("%d%d",&n,&m);
    int u,v,t;
    for(int i=;i<=m;i++){
        scanf("%d%d",&u,&v);
        insert(u,v);
        insert(v,u);
    }
    for(int i=;i<=n;i++){
        if(!dfn[i])tarjan(i,i);
    }
    for(int i=;i<=n;i++){
        if(cut[i])mx++;
    }
    printf("%d\n",mx);
    for(int i=;i<=n;i++){
        if(cut[i]){
            printf("%d ",i);
        }
    }
    return ;
}