由Leetcode详解算法 之 动态规划（DP）

因为最近一段时间接触了一些Leetcode上的题目，发现许多题目的解题思路相似，从中其实可以了解某类算法的一些应用场景。

这个随笔系列就是我尝试的分析总结，希望也能给大家一些启发。

动态规划的基本概念

一言以蔽之，动态规划就是将大问题分成小问题，以迭代的方式求解。

可以使用动态规划求解的问题一般有如下的两个特征：

1、有最优子结构（optimal substructure）

即待解决问题的最优解能够通过求解子问题的最优解得到。

2、子问题间有重叠（overlapping subproplems）

即同样的子问题在求解过程中会被多次调用，而不是在求解过程中不断产生新的子问题。动态规划一般会将子问题的解暂时存放在一个表中，以方便调用。（这也是动态规划与分治法之间的区别）

下图是斐波那契数列求解的结构图，它并非是“树状”，也就是说明其子问题有重叠。

动态规划的一般过程

1、分析得到结果的过程，发现子问题（子状态）；

2、确定状态转移方程，即小的子问题与稍大一些的子问题间是如何转化的。

以斐波那契为例（两种方式：自顶向下与自底向上）

以求解斐波那契数列为例，我们很容易得到求解第N项的值的子问题是第i项（i＜N）的值。

而状态转移方程也显而易见：f(n) = f(n-1) + f(n-2)

由此我们可以得到相应迭代算法表达：

function fib()
	if n <= 1 return n
   return fib(n - 1) + fib(n - 2)

不过，如之前所说，动态规划一个特点就是会存储子问题的结果以避免重复计算，（我们将这种方式称作memoization）通过这种方式，可以使时间复杂度减小为O(N)，不过空间复杂度因此也为O(N)。我们可以使用一个映射表（map）存储子问题的解:

var m := map(0 -> 0, 1 -> 1)
function fib(n)
	if key n is not in map m
		m[n] := fib(n - 1) + fib(n - 2)
   return m[n]

上面的方式是自顶向下（Top-down）方式的，因为我们先将大问题“分为”子问题，再求解/存值；

而在自底向上（Bottom-up）方式中，我们先求解子问题，再在子问题的基础上搭建出较大的问题。（或者，可以视为“迭代”(iterative)求解）通过这种方法的空间复杂度为O(1)，而并非自顶向下方式的O(N)，因为采用这种方式不需要额外的存值。

function fib(n)
	if n = 0
    	return 0
   else
   		var previousFib := 0, currentFib := 1
		 repeat n - 1 times
		 	var newFib := previousFib + currentFib
			previousFib := currentFib
			currentFib 	:= newFib
	return currentFib

动态规划与其他算法的比较

动态规划与分治法

分治法（Divide and Conquer）的思想是：将大问题分成若干小问题，每个小问题之间没有关系，再递归的求解每个小问题，比如排序算法中的“归并排序”和“快速排序”；

而动态规划中的不同子问题存在一定联系，会有重叠的子问题。因此动态规划中已求解的子问题会被保存起来，避免重复求解。

动态规划与贪心算法

贪心算法（greedy algorithm）无需求解所有的子问题，其目标是寻找到局部的最优解，并希望可以通过“每一步的最优”得到整体的最优解。

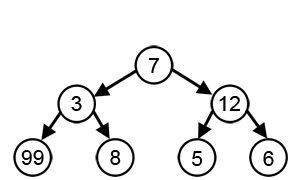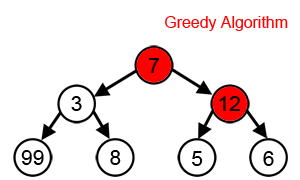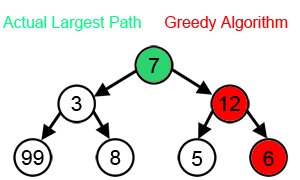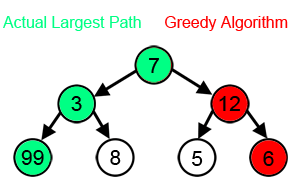
如果把问题的求解看作一个树状结构，动态规划会考虑到树中的每一个节点，是可回溯的；而贪心算法只能在每一步的层面上做出最优判断，“一条路走到黑”，是“一维”的。因此贪心算法可以看作是动态规划的一个特例。

那么有没有“一条路走到黑”，最后的结果也是最优解的呢？

当然有，比如求解图的单源最短路径用到的Dijkstra算法就是“贪心”的：每一次都选择最短的路径加入集合。而最后得到的结果也是最优的。（这和路径问题的特殊性质也有关系，因为如果路径的权值非零，很容易就能得到路径递归的结果“单增”）

Leetcode例题分析

Unique Binary Search Trees （Bottom-up）

96. Unique Binary Search Trees

Given n, how many structurally unique BST's (binary search trees) that store values 1 ... n?

给定n，求节点数为n的排序二叉树（BST）共有几种（无重复节点）。

思路

可以令根节点依次为节点1~n，比根节点小的组成左枝，比根节点大的组成右枝。

子树亦可根据此方法向下分枝。递归求解。

算法

令G(n)为长度为n的不同排序树的数目（即目标函数）；

令F(i,n)为当根节点为节点i时，长度n的不同排序树的数目。

对于每一个以节点i为根节点的树，F(i,n)实际上等于其左子树的G(nr)乘以其右子树的G(nl);

因为这相当于在两个独立集合中各取一个进行排列组合，其结果为两个集合的笛卡尔乘积

我们由此可以得到公式F(i,n) = G(i-1)*G(n-i)

从而得到G(n)的递归公式：

G(n) = ΣG(i-1)G(n-i)

算法实现

class Solution {
    public int numTrees(int n) {
        int[] G = new int[n+1];
        G[0] = 1;
        G[1] = 1;

        for(int i = 2; i <= n; ++i){
            for(int j = 1; j <= i; ++j){
                G[i] += G[j - 1] * G[i - j];
            }
        }
        return G[n];
    }
}

一个典型的“自底向上”的动态规划问题。

当然，由于通过递推公式可以由数学方法得到G(n)的计算公式，直接使用公式求解也不失为一种方法。

Coin Change （Top-down）

322. Coin Change

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

coins数组表示每种硬币的面值，amount表示钱的总数，若可以用这些硬币可以组合出给定的钱数，则返回需要的最少硬币数。无法组合出给定钱数则返回-1。

算法思路

1、首先定义一个函数F(S) 对于amount S 所需要的最小coin数

2、将问题分解为子问题：假设最后一个coin面值为C 则F(S) = F(S - C) + 1

S - ci >= 0 时，设F(S) = min[F(S - ci)] + 1 (选择子函数值最小的子函数，回溯可得到总体coin最少)

S == 0 时，F(S) = 0;

n == 0 时，F(S) = -1

算法实现

class Solution {
    public int coinChange(int[] coins, int amount) {
        if(amount < 1) return 0;
        return coinChange(coins, amount, new int[amount]);
    }

    private int coinChange(int[] coins, int rem, int[] count)
    {
        if(rem < 0) return -1;
        if(rem == 0) return 0;
        if(count[rem - 1]!=0) return count[rem - 1]; //这里的rem-1 其实就相当于 rem 从 0 开始计数(不浪费数组空间)
        int min = Integer.MAX_VALUE; //每次递归都初始化min
        for(int coin : coins){
            int res = coinChange(coins, rem - coin, count); //计算子树值
            if(res >= 0 && res < min)
                min = 1 + res; //父节点值 = 子节点值+1 （这里遍历每一种coin之后得到的最小的子树值）
        }
        count[rem - 1] = (min == Integer.MAX_VALUE) ? -1:min; //最小值存在count[rem-1]里，即这个数值(rem)的最小钱币数确定了
        return count[rem-1];
    }
}

算法采用了动态规划的“自顶向下”的方式，使用了回溯法(backtracking)，并且对于回溯树进行剪枝（coin面值大于amount时）。

同时，为了降低时间复杂度，将已计算的结果（一定面值所需要的最少coin数）存储在映射表中。

虽然动态规划是钱币问题的一般认为的解决方案，然而实际上，大部分的货币体系（比如美元/欧元）都是可以通过“贪心算法”就能得到最优解的。

最后，如果大家对于文章有任何意见/建议/想法，欢迎留言讨论！