【原创 深度学习与TensorFlow 动手实践系列 - 2】第二课：传统神经网络

第二课 传统神经网络

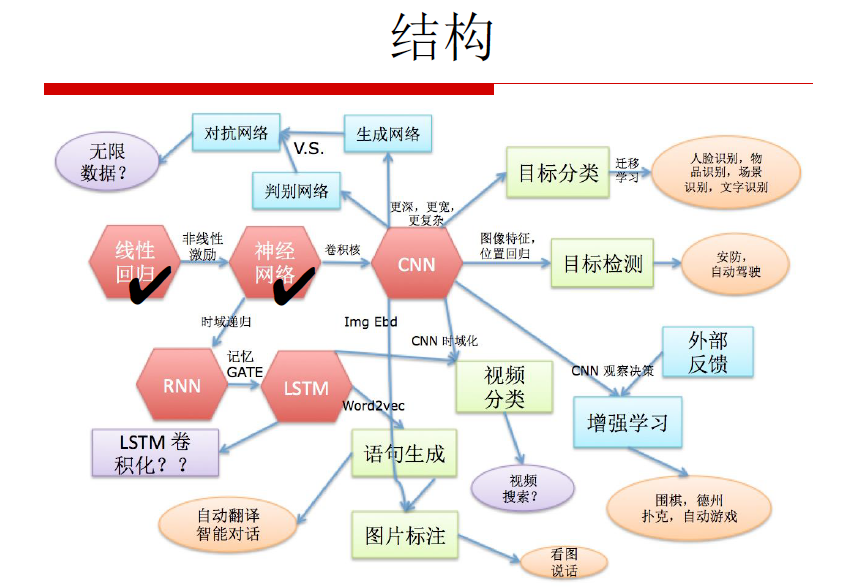
《深度学习》整体结构：

线性回归 -> 神经网络 -> 卷积神经网络（CNN）-> 循环神经网络（RNN）- LSTM

目标分类（人脸识别，物品识别，场景识别，文字识别），目标检测（安防，自动驾驶），视频分类（视频检索），语句生成（自动翻译，智能对话）

提纲：

1. 神经网络起源：线性回归

2. 从线性到非线性

3. 神经网络的构建

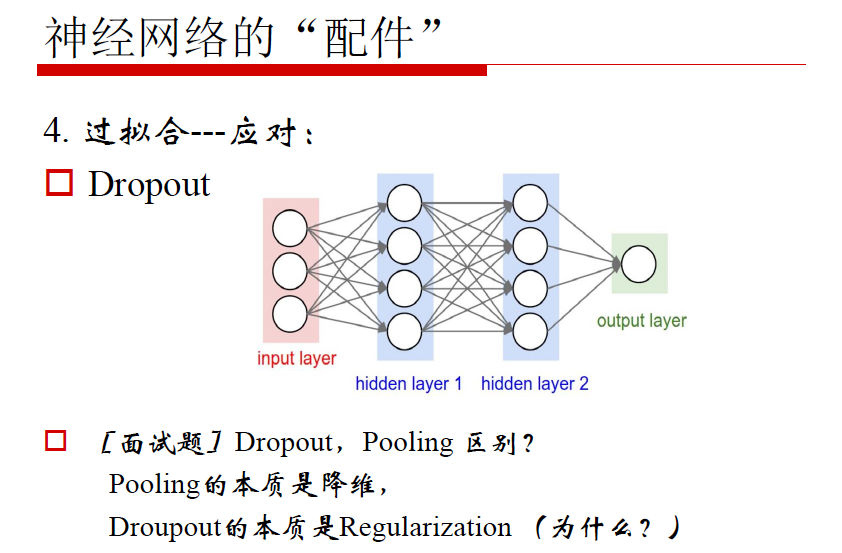
4. 神经网络的“配件”

 期待目标：

1. 了解从线性到非线性回归的转化

2. 明白如何构建神经网络，了解不同激励函数的区别联系

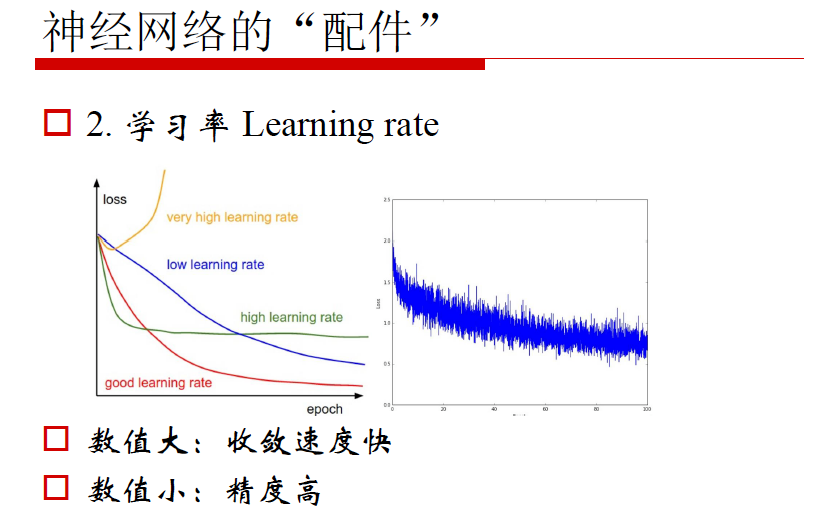
3. 掌握“配件”对神经网络性能的影响（损失函数 Cost，学习率 Learning Rate，动量，过拟合），会“调参”

4. 明白本节所有的“面试题”

线性回归：

1. 概念：线性关系来描述输入到输出的映射关系

2. 应用场景：网络分析，银行风险分析，基金股价预测，天气预报

线性回归：

一个线性回归问题

目标方程：y = ax1 + bx2 + cx3 + d

参数： m = [a, b, c, d]

数据：[(x1,1, x2,1,x3,1), (), (), ()]

预测：yt = ax1,t + bx2,t + cx3,t + d

目标：minimize (yt - yt)

总结：线性函数是一维函数，y = ax1 + bx2 + cx3 + d

现在要计算最佳参数 m = [a, b, c, d]

给定数据，计算出预测值，预测值与真实值计算Cost，当Cost最小的时候计算出 m = [a, b, c, d]

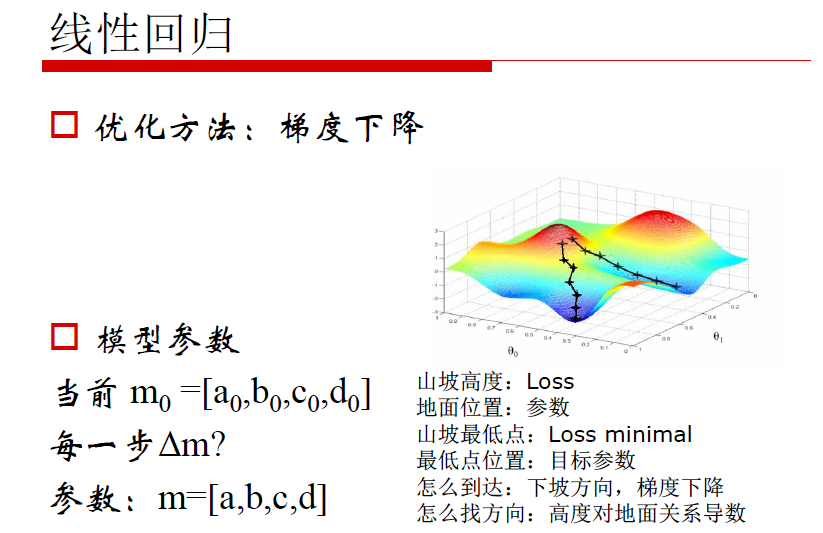
优化方法：梯度下降法

模型参数

当前 m0 = [a0, b0, c0, d0]

每一步 m?

参数 m = [a, b, c, d]

梯度下降：梯度计算

Loss = ax1 + bx2 + cx3 + d -y

梯度下降：参数更新

梯度下降法总结：

1. 随机初始化参数

开启循环 t= 0, 1, 2

带入数据求出结果 yt

与真值比较得到loss = y - yt

对各个变量求导得到 m

更新变量 m

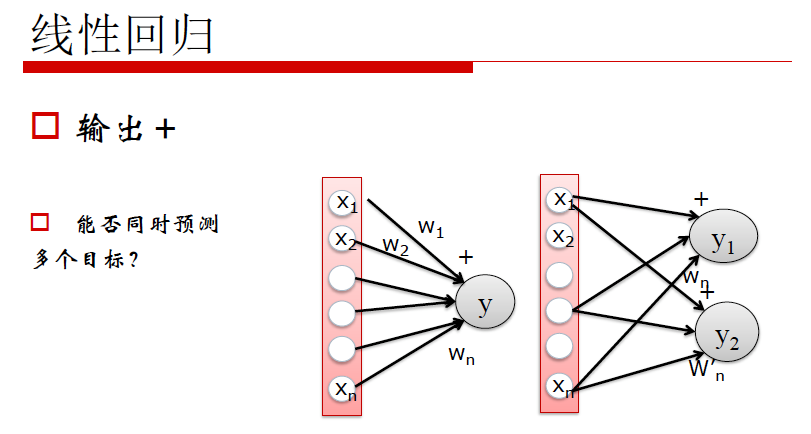
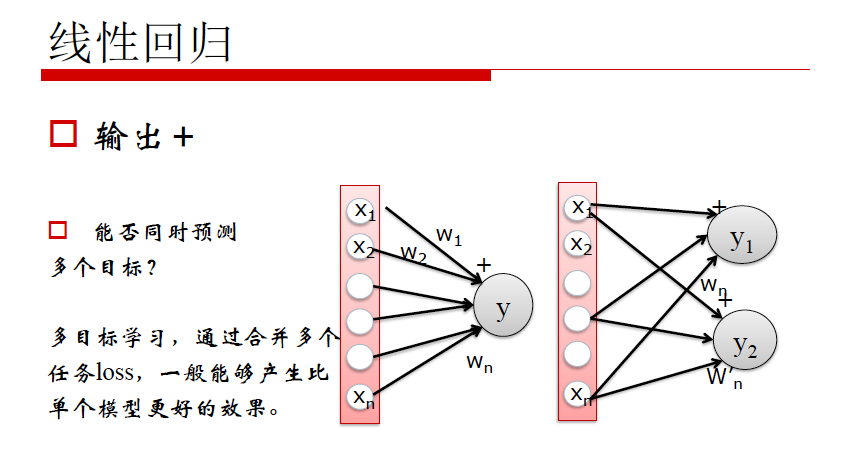
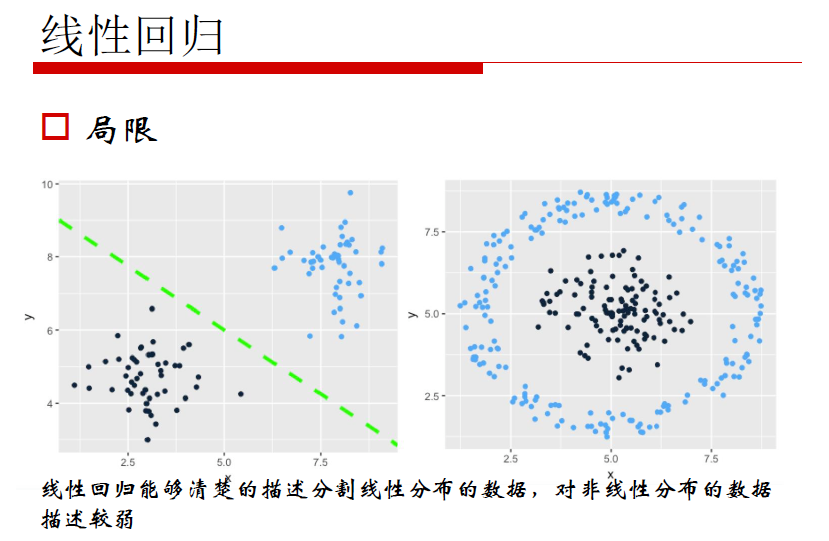
线性回归的局限性：线性回归能够清楚的描述分割线性分布的数据，对非线性分布的数据描述较弱

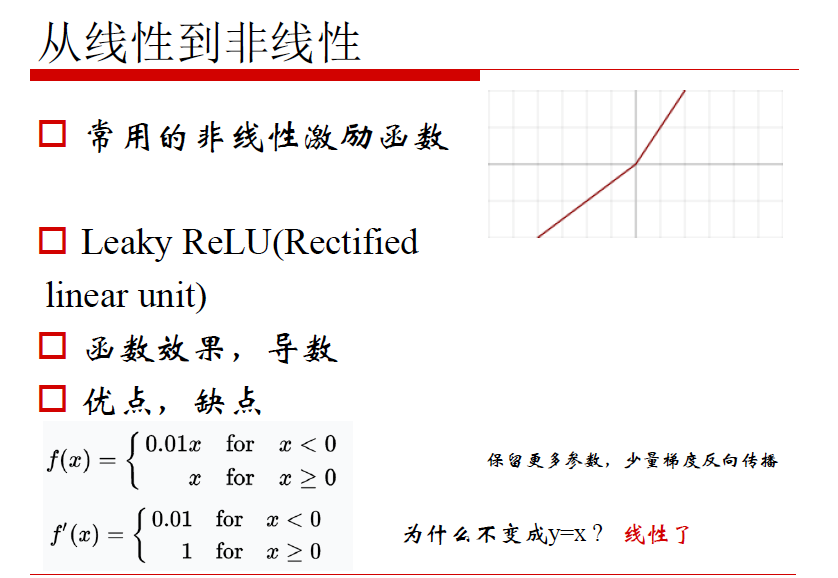
非线性激励

考量标准：

1. 正向对输入的调整

2. 反向梯度损失

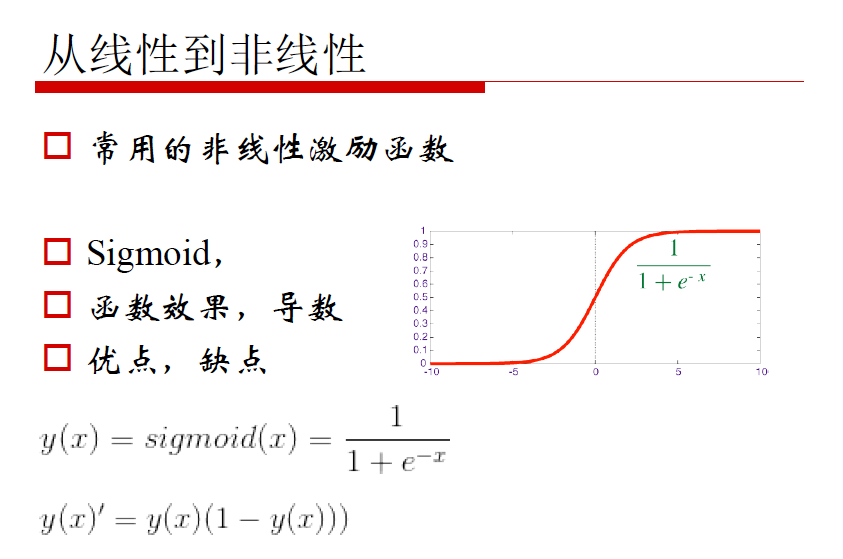
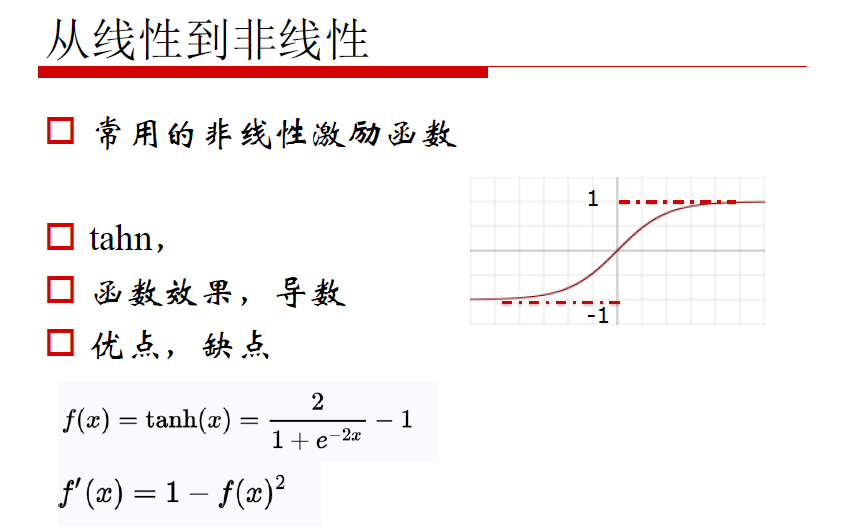
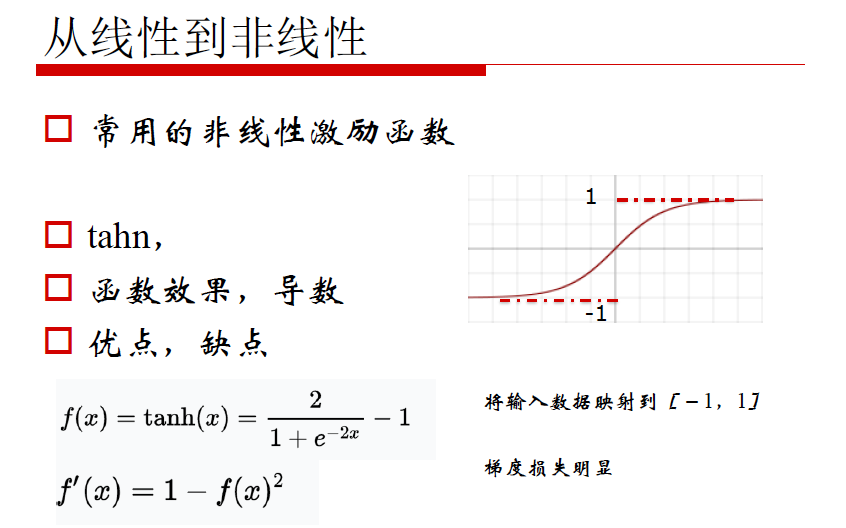
神经网络构建

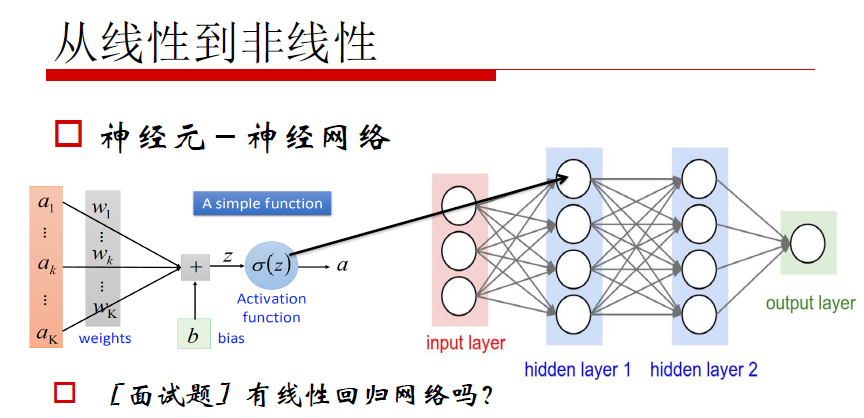
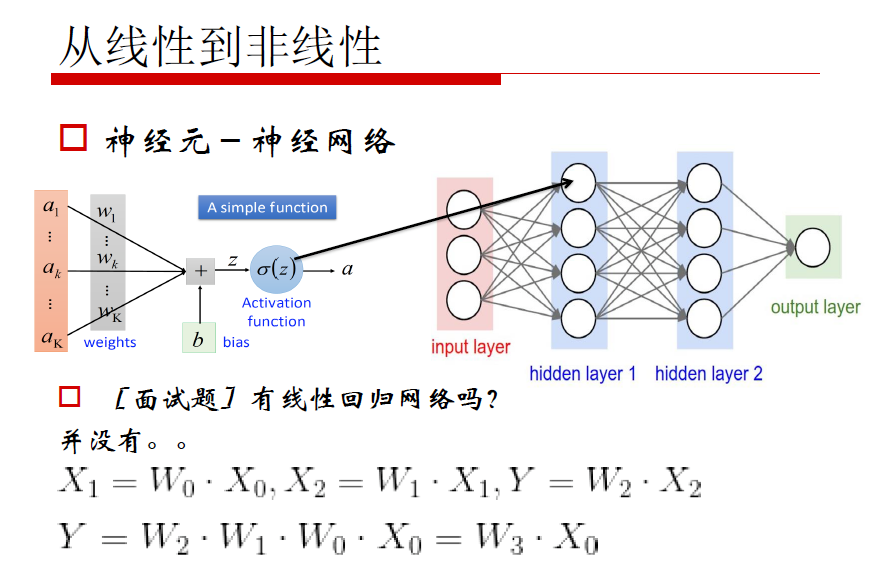
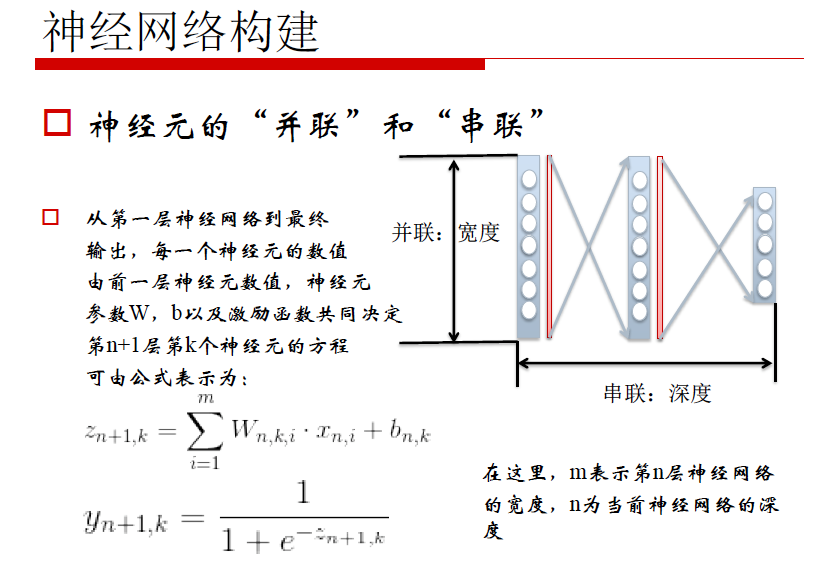
神经元的“并联”和“串联”

从第一层神经网络到最终输出，每一个神经元的数值由前一层神经元数值，神经元参数W，b以及激励函数共同决定第n+1层，第k个神经元的方程，可由公式表示为：

在这里，m表示第n层神经网络的宽度，n为当前神经网络的深度

并联：深度，串联：宽度

MINIST 神经网络分类：

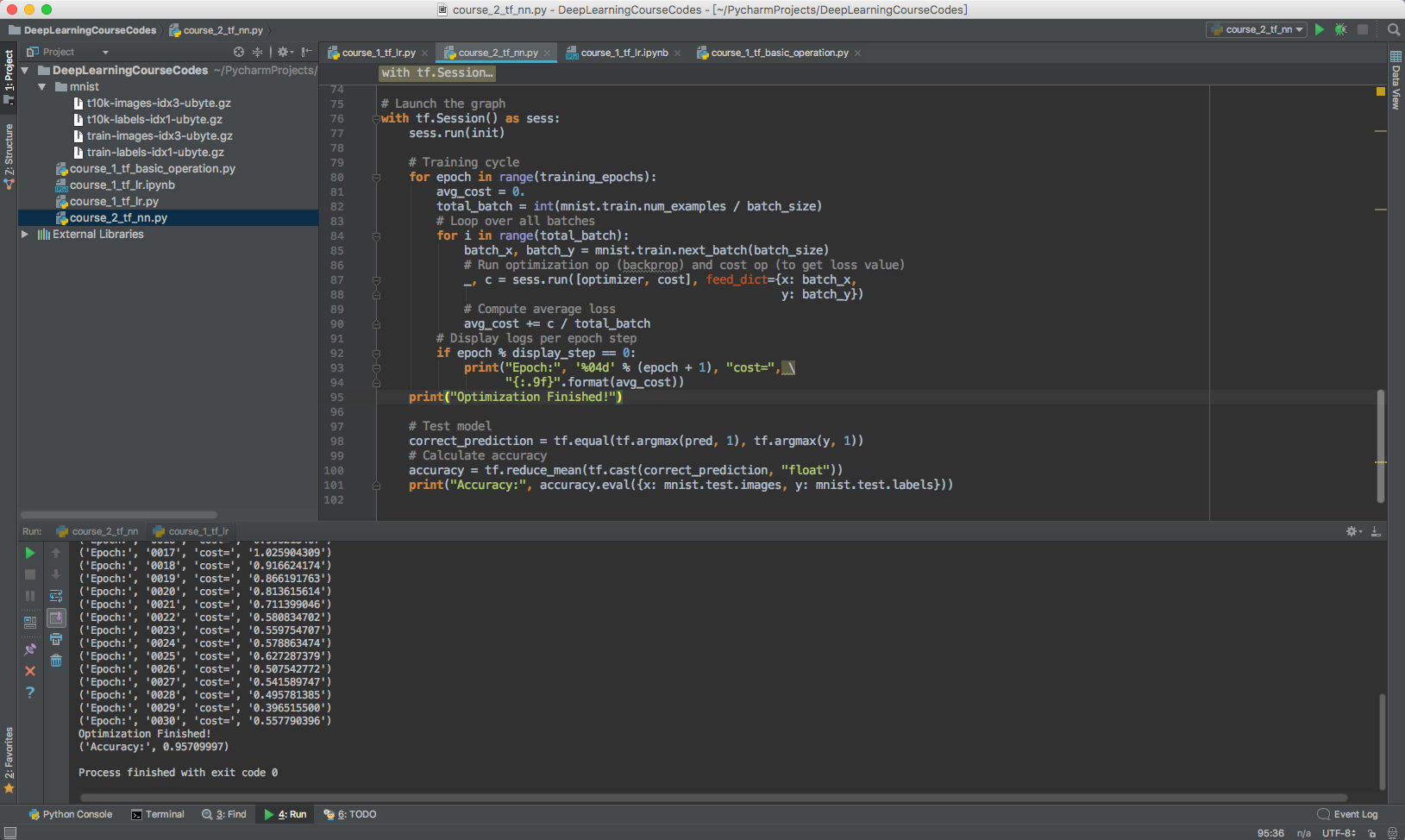
course_2_tf_nn.py

结构变化影响：

1. “并联”宽度影响

2. “串联”层数影响

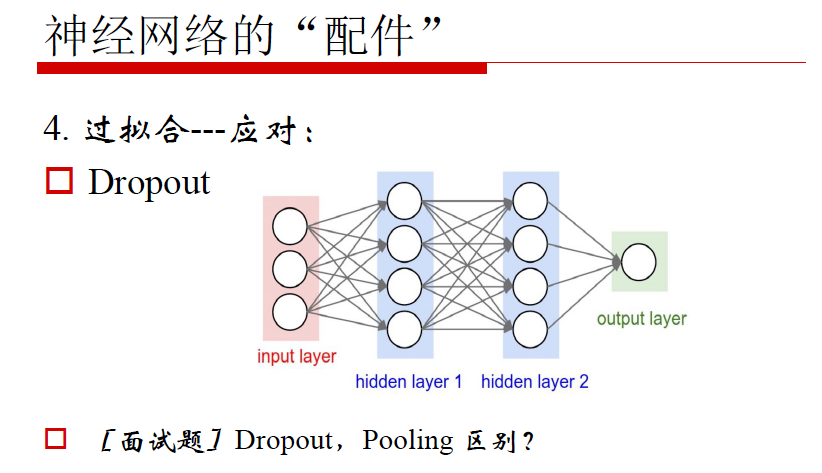
3. Dropout

4. Learning rate

1. 损失函数 - Loss

影响深度学习性能最重要因素之一。是外部世界对神经网络模型训练的直接指导。

合适的损失函数能够确保深度学习模型收敛

设计合适的损失函数是研究工作的主要内容之一

总结：

1. 神经网络起源：线性回归

2. 从线性到非线性

3. 神经网络的构建

4. 神经网络的“配件”

下节课预告：链式规则反向求导，SGD优化原理，卷积神经网络（CNN）各个layers介绍

第二节课的代码

https://github.com/wiibrew/DeepLearningCourseCodes/blob/master/course_2_tf_nn.py

https://github.com/wiibrew/DeepLearningCourseCodes/blob/master/course_2_tf_nn.ipynb

具体通过TensorFlow构建神经网络的过程，通过Pycharm和 Python Notebook来完成实验，调参还部署很熟练。

TensorFlow 对数据进行简单的可视化实验：

 http://playground.tensorflow.org/