奇异值分解（SVD）与在降维中的应用

　　奇异值分解(Singular Value Decomposition，SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。本文就对SVD的原理做一个总结，并讨论在在PCA降维算法中是如何运用运用SVD的。

1. 特征值和特征向量

　　特征值和特征向量的定义如下：

　　Ax=λx

　　其中A是一个n×n的矩阵，x是一个n维向量，则我们说λ是矩阵A的一个特征值，而x是矩阵A的特征值λ所对应的特征向量。

　　求出特征值和特征向量有什么好处呢？ 就是我们可以将矩阵A特征分解。如果我们求出了矩阵A的n个特征值λ1≤λ2≤...≤λn,以及这n个特征值所对应的特征向量{w1,w2,...wn}，那么矩阵A就可以用下式的特征分解表示：A=WΣW⁻¹

　　其中W是这n个特征向量所张成的n×n维矩阵，而Σ为这n个特征值为主对角线的n×n维矩阵。

　　一般我们会把W的这n个特征向量标准化，即满足||wi||²=1, 或者说wi^Twi=1，此时W的n个特征向量为标准正交基，满足W^TW=I，即W^T=W⁻¹, 也就是说W为酉矩阵。

　　这样我们的特征分解表达式可以写成： A=WΣW^T

　　注意到要进行特征分解，矩阵A必须为方阵。那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了。

2.  SVD的定义

　　SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为：A=UΣV^T

　　其中U是一个m×m的矩阵，Σ是一个m×n的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，V是一个n×n的矩阵。U和V都是酉矩阵，即满足U^TU=I,V^TV=I。下图可以很形象的看出上面SVD的定义：

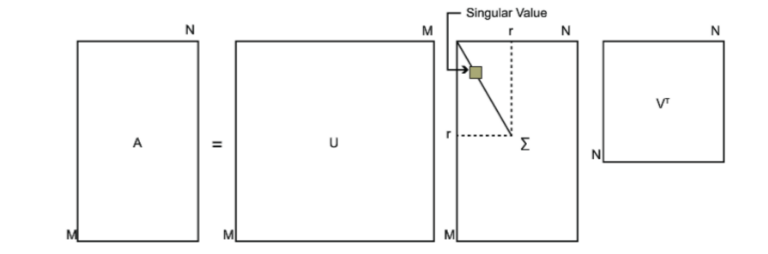
　　那么我们如何求出SVD分解后的U,Σ,V这三个矩阵呢？

　　如果我们将A的转置和A做矩阵乘法，那么会得到n×n的一个方阵A^TA。既然A^TA是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足：(A^TA)v_i=λ_iv_i

　　这样我们就可以得到矩阵A^TA的n个特征值和对应的n个特征向量v了。将A^TA的所有特征向量张成一个n×n的矩阵V，就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。

　　如果我们将A和A的转置做矩阵乘法，那么会得到m×m的一个方阵AA^T。既然AA^T是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足：(AA^T)u_i=λ_iu_i

　　这样我们就可以得到矩阵AA^T的m个特征值和对应的m个特征向量u了。将AA^T的所有特征向量张成一个m×m的矩阵U，就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。

　　U和V都求出来了，现在就剩下奇异值矩阵Σ没有求出了。由于Σ除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值σ就可以了。我们注意到:

　　A=UΣV^T ⇒ AV=UΣV^TV ⇒ AV=UΣ ⇒ Av_i=σ_iu_i ⇒ σ_i=Av_i/u_i

　 这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵Σ。

　　上面还有一个问题没有讲，就是我们说A^TA的特征向量组成的就是我们SVD中的V矩阵，而AA^T的特征向量组成的就是我们SVD中的U矩阵，这有什么根据吗？这个其实很容易证明，我们以V矩阵的证明为例。A=UΣV^T ⇒ A^T=VΣ^TU^T ⇒ A^TA=VΣ^TU^TUΣV^T=VΣ²V^T

　　上式证明使用了:U^TU=I,Σ^TΣ=Σ²。U^TU=I,Σ^TΣ=Σ²。可以看出A^TA的特征向量组成的就是SVD中的V矩阵。类似的方法可以得到AA^T的特征向量组成的就是SVD中的U矩阵。

　　进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：σ_i=√λ_i

　　这样也就是说，我们可以不用σ_i=Av_i/u_i来计算奇异值，也可以通过求出A^TA的特征值取平方根来求奇异值。

3. SVD的一些性质

　　上面几节我们对SVD的定义和计算做了详细的描述，似乎看不出我们费这么大的力气做SVD有什么好处。那么SVD有什么重要的性质值得我们注意呢？

　　对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：A_m×n=U_m×mΣ_m×nV^T_n×n≈U_m×kΣ_k×kV^T_k×n。其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵U_m×k,Σ_k×k,V^T_k×n来表示。如下图所示，现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。

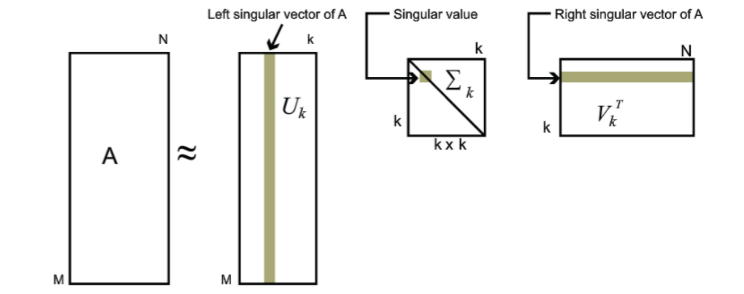
　　由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。下面我们就对SVD用于PCA降维做一个介绍。

4. SVD用于PCA

　　在主成分分析（PCA）中，要用PCA降维，需要找到样本协方差矩阵X^TX的最大的d个特征向量，然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵X^TX，当样本数多、样本特征数也多的时候，这个计算量是很大的。

　　注意到我们的SVD也可以得到协方差矩阵X^TX最大的d个特征向量组成的矩阵，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵X^TX，也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。

　　另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？

　　假设我们的样本是m×n的矩阵X，如果我们通过SVD找到了矩阵XX^T最大的d个特征向量组成的m×d维矩阵U，则我们如果进行如下处理：X′_d×n=U^T_d×mX_m×n

　　可以得到一个d×n的矩阵X‘,这个矩阵和我们原来的m×n维样本矩阵X相比，行数从m减到了k，可见对行数进行了压缩。也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。　　　　

5. SVD小结　

　　SVD作为一个很基本的算法，在很多机器学习算法中都有它的身影，特别是在现在的大数据时代，由于SVD可以实现并行化，因此更是大展身手。SVD的原理不难，只要有基本的线性代数知识就可以理解，实现也很简单因此值得仔细的研究。当然，SVD的缺点是分解出的矩阵解释性往往不强，有点黑盒子的味道，不过这不影响它的使用。

文章内容转载自：https://www.cnblogs.com/pinard/p/6251584.html