梯度下降（gradient descent），是一种用于最优化（通常是最小化），代价函数/损失函数/目标函数/误差函数/准则，的方法。 不过，最值有时很难找到，尤其是在高维情况下，所以常常把局部最优解看作全局最优解。

1、导数

f(x)在x处的斜率。

2、临界点（critical point）/驻点（stationary point）

导数为0，包括局部极小点、局部极大点、鞍点。

3、偏导数（partial derivative）

f(x)关于多维输入x的其中一维xi的导数。

4、方向导数（directional derivative）

导数和偏导数只能描述坐标轴方向的变化率。但是一个点在无数个方向上都有变化率，这时候就需要方向导数了：f(x)在某个向量方向上的导数。

5、梯度

梯度是一个向量，向量的第i个元素是f(x)关于xi的偏导数。临界点是梯度中所有元素都为0的点。

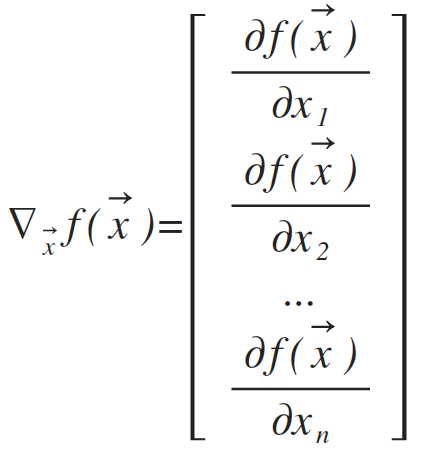
6、学习率（learning rate）

爬山算法

参考链接：

https://www.zhihu.com/question/36301367

https://zhuanlan.zhihu.com/p/38525412

https://mp.weixin.qq.com/s?__biz=MzI4MDYzNzg4Mw==&mid=2247483704&idx=1&sn=8f0c6e33ef84c26823e562be16bce684&chksm=ebb439ecdcc3b0fa4e9571deb33ccea62e42034c88db4e190633588307dce4a1e0c91ed2635c&scene=21#wechat_redirect

AI 梯度下降的更多相关文章

  1. [AI]神经网络章2　神经网络中反向传播与梯度下降的基本概念

    反向传播和梯度下降这两个词,第一眼看上去似懂非懂,不明觉厉.这两个概念是整个神经网络中的重要组成部分,是和误差函数/损失函数的概念分不开的. 神经网络训练的最基本的思想就是:先“蒙”一个结果,我们叫预 ...

  2. AI 随机梯度下降（SGD）

    随机梯度下降(stochastic gradient descent) 梯度是期望 计算梯度耗时太长

  3. 机器学习算法整理（二）梯度下降求解逻辑回归 python实现

    逻辑回归(Logistic regression) 以下均为自己看视频做的笔记,自用,侵删! 还参考了:http://www.ai-start.com/ml2014/ 用梯度下降求解逻辑回归 Logi ...

  4. 【深度学习】线性回归（Linear Regression）——原理、均方损失、小批量随机梯度下降

    1. 线性回归 回归(regression)问题指一类为一个或多个自变量与因变量之间关系建模的方法,通常用来表示输入和输出之间的关系. 机器学习领域中多数问题都与预测相关,当我们想预测一个数值时,就会 ...

  5. 梯度下降（Gradient Descent）小结

    在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法.这里就对梯度下降法做一个完整的总结. 1. 梯度 在微 ...

  6. 从梯度下降到Fista

    前言: FISTA(A fast iterative shrinkage-thresholding algorithm)是一种快速的迭代阈值收缩算法(ISTA).FISTA和ISTA都是基于梯度下降的 ...

  7. 线性回归、梯度下降（Linear Regression、Gradient Descent）

    转载请注明出自BYRans博客:http://www.cnblogs.com/BYRans/ 实例 首先举个例子,假设我们有一个二手房交易记录的数据集,已知房屋面积.卧室数量和房屋的交易价格,如下表: ...

  8. 随机梯度下降（Stochastic gradient descent）和 批量梯度下降（Batch gradient descent ）的公式对比、实现对比[转]

    梯度下降(GD)是最小化风险函数.损失函数的一种常用方法,随机梯度下降和批量梯度下降是两种迭代求解思路,下面从公式和实现的角度对两者进行分析,如有哪个方面写的不对,希望网友纠正. 下面的h(x)是要拟 ...

  9. 为什么是梯度下降？SGD

    在机器学习算法中,为了优化损失函数loss function ,我们往往采用梯度下降算法来进行优化.举个例子: 线性SVM的得分函数和损失函数分别为:                         ...

随机推荐

  1. PHP: Browser, Operating System (OS), Device, and Language Detect

    https://github.com/sinergi/php-browser-detector Device.php: <!DOCTYPE html> <html> <h ...

  2. csharp: DefaultValueAttribute Class

    public class CalendarEvent { public int id { get; set; } public string title { get; set; } public st ...

  3. vue 父子组件互相传值容易出现的报错

    对于父子组件之间的互相传值,报错如下: [Vue warn]: Avoid mutating a prop directly since the value will be overwritten w ...

  4. Oracle 常用的查询操作

    –1. 查询系统所有对象select owner, object_name, object_type, created, last_ddl_time, timestamp, statusfrom db ...

  5. Android项目实战（三十二）：圆角对话框Dialog

    前言: 项目中多处用到对话框,用系统对话框太难看,就自己写一个自定义对话框. 对话框包括:1.圆角 2.app图标 , 提示文本,关闭对话框的"确定"按钮 难点:1.对话框边框圆角 ...

  6. 《InsideC#》笔记(十) 异常处理

    CLR的作用之一是处理异常.通过自动的内存和资源管理可以避免一部分异常,然后借助强类型系统还可以捕获运行时异常. 一 异常基础 异常处理系统保护四个关键字:try,catch,throw,finall ...

  7. Sqlserver精简安装选项

  8. vs2012碰到生成时报该错误：项目中不存在目标“GatherAllFilesToPublish”

    手头一个vs2010升级到vs2012后,web项目发布到本地目录时项目报错:“该项目中不存在目标“GatherAllFilesToPublish”” 通过谷歌大神的帮助,找到了解决方法.共享之. 原 ...

  9. React 表单与事件

    一个简单是实例 在实例中我们设置了输入框 input 值value = {this.state.data}.在输入框值发生变化时我们可以更新 state.我们可以使用 onChange 事件来监听 i ...

  10. [20171120]bash使用here documents的一个小细节.txt

    [20171120]bash使用here documents的一个小细节.txt --//昨天看bash文档,,发现一些小细节,做一个记录,就是EOF加引号的问题. command <<' ...