POJ 2826 An Easy Problem?!

An Easy Problem?!

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 7837		Accepted: 1145

Description

It's raining outside. Farmer Johnson's bull Ben wants some rain to water his flowers. Ben nails two wooden boards on the wall of his barn. Shown in the pictures below, the two boards on the wall just look like two segments on the plane, as they have the same width. 

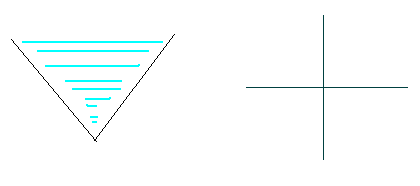
Your mission is to calculate how much rain these two boards can collect. 

Input

The first line contains the number of test cases. 
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x₁, y₁, x₂, y₂, x₃, y₃, x₄, y₄. (x₁, y₁), (x₂, y₂) are the endpoints of one board, and (x₃, y₃), (x₄, y₄) are the endpoints of the other one. 

Output

For each test case output a single line containing a real number with precision up to two decimal places - the amount of rain collected. 

Sample Input

2
0 1 1 0
1 0 2 1

0 1 2 1
1 0 1 2

Sample Output

1.00
0.00

Source

POJ Monthly--2006.04.28, Dagger@PKU_RPWT

 

 

 

 

 

需要想到好几种特殊情况。

 

线段不相交，结果为0.

有一条线段平行于x轴结果也为0；

 

尤其是第三种情况，很难想到。

 

#include <stdio.h>
#include <math.h>
#include <algorithm>
#include <string.h>
#include <math.h>
using namespace std;

const double eps = 1e-;
int sgn(double x)
{
    if(fabs(x) < eps)return ;
    if(x < )return -;
    else return ;
}
struct Point
{
    double x,y;
    Point(){}
    Point(double _x,double _y)
    {
        x = _x;y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x,y - b.y);
    }
    //叉积
    double operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
    //点积
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
};
struct Line
{
    Point s,e;
    Line(){}
    Line(Point _s,Point _e)
    {
        s = _s;e = _e;
    }
    //两直线相交求交点
    //第一个值为0表示直线重合，为1表示平行，为0表示相交,为2是相交
    //只有第一个值为2时，交点才有意义
    pair<int,Point> operator &(const Line &b)const
    {
        Point res = s;
        if(sgn((s-e)^(b.s-b.e)) == )
        {
            if(sgn((s-b.e)^(b.s-b.e)) == )
                return make_pair(,res);//重合
            else return make_pair(,res);//平行
        }
        double t = ((s-b.s)^(b.s-b.e))/((s-e)^(b.s-b.e));
        res.x += (e.x-s.x)*t;
        res.y += (e.y-s.y)*t;
        return make_pair(,res);
    }
};

//*判断线段相交
bool inter(Line l1,Line l2)
{
    return
    max(l1.s.x,l1.e.x) >= min(l2.s.x,l2.e.x) &&
    max(l2.s.x,l2.e.x) >= min(l1.s.x,l1.e.x) &&
    max(l1.s.y,l1.e.y) >= min(l2.s.y,l2.e.y) &&
    max(l2.s.y,l2.e.y) >= min(l1.s.y,l1.e.y) &&
    sgn((l2.s-l1.e)^(l1.s-l1.e))*sgn((l2.e-l1.e)^(l1.s-l1.e)) <=  &&
    sgn((l1.s-l2.e)^(l2.s-l2.e))*sgn((l1.e-l2.e)^(l2.s-l2.e)) <= ;
}

int main()
{
    int x1,y1,x2,y2,x3,y3,x4,y4;
    int T;
    Line l1,l2;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d%d%d%d%d%d%d",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);
        l1 = Line(Point(x1,y1),Point(x2,y2));
        l2 = Line(Point(x3,y3),Point(x4,y4));
        if(sgn(l1.s.y-l1.e.y)== || sgn(l2.s.y-l2.e.y) == )
        {
            printf("0.00\n");
            continue;
        }
        if(sgn(l1.s.y-l1.e.y) < )swap(l1.s,l1.e);
        if(sgn(l2.s.y-l2.e.y) < )swap(l2.s,l2.e);
        if(inter(l1,l2) == false)
        {
            printf("0.00\n");
            continue;
        }
        //口被封掉的情况
        if(inter(Line(l1.s,Point(l1.s.x,)),l2) )
        {
            printf("0.00\n");
            continue;
        }
        //口被封掉
        if(inter(Line(l2.s,Point(l2.s.x,)),l1) )
        {
            printf("0.00\n");
            continue;
        }
        pair<int,Point>pr;
        pr = l1 & l2;
        Point p = pr.second;
        double ans1;
        pr = l1 & Line(Point(,l2.s.y),l2.s);
        Point p1 = pr.second;
        ans1 = fabs( (l2.s-p)^(p1-p) )/;
        double ans2;
        pr = l2 & Line(Point(,l1.s.y),l1.s);
        Point p2 = pr.second;
        ans2 = fabs( (l1.s-p)^(p2-p) )/;
        printf("%.2lf\n",min(ans1,ans2));
    }
    return ;
}