Machine Learning in Action -- 树回归

前面介绍线性回归，但实际中，用线性回归去拟合整个数据集是不太现实的，现实中的数据往往不是全局线性的
当然前面也介绍了局部加权线性回归，这种方法有些局限

这里介绍另外一种思路，树回归
基本思路，用决策树将数据集划分成若干个子集，然后再子集上再用线性回归进行拟合

决策树是种贪心算法，最简单典型的决策树算法是ID3
ID3，每次都选取最佳特征来进行划分，并且按照特征的取值来决定划分的个数，比如性别，就划分为男，女
在决定最佳特征时，用香农熵作为指标，表示当前的划分是否会让数据更加有序

ID3的局限是，
首先特征只能是离散值
并且划分过于迅速，即分的太细
只能用于分类问题

所以CART（Classification And Regression Trees）决策树算法，更加实用，从名字就可以看出，既可以用于分类问题也可以用于回归问题
其实CART和ID3比，最大的区别就是，在特征划分时，采用二分，这样就很容易处理连续型特征，并且划分速度相对较慢

 

回归树

下面就看看对于连续型特征的回归树的构建算法，回归树，即叶节点是具体的数值

def binSplitDataSet(dataSet, feature, value):
    mat0 = dataSet[nonzero(dataSet[:,feature] > value)[0],:][0]
    mat1 = dataSet[nonzero(dataSet[:,feature] <= value)[0],:][0]
    return mat0,mat1

def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
    feat, val = chooseBestSplit(dataSet, leafType, errType, ops)
    if feat == None: return val
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    lSet, rSet = binSplitDataSet(dataSet, feat, val)
    retTree['left'] = createTree(lSet, leafType, errType, ops)
    retTree['right'] = createTree(rSet, leafType, errType, ops)
    return retTree

首先给出回归树的通用算法，

1. binSplitDataSet

对于数据集的二分函数，这个实现很难理解，我自己实现了一个，

def binSplitDataSet(dataSet, feature, value):
    m = dataSet[:,feature].T >value
    m = m.getA()[0]  #将numpy.matrix转换为numpy.array
    mat0 = dataSet[m]
    mat1 = dataSet[-m]
    return mat0,mat1

用numpy的boolean indexing很容易实现

2. createTree

Tree的每个节点，划分特征，划分值，左子树，右子树

所以最关键的是chooseBestSplit，这个函数会找出最佳的特征和划分值，当碰到叶节点时，返回叶节点的值

 

接着给出chooseBestSplit的实现，

def regLeaf(dataSet):
    return mean(dataSet[:,-1])

def regErr(dataSet):
    return var(dataSet[:,-1]) * shape(dataSet)[0]

def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
    tolS = ops[0]   #最小误差下降值，划分后的误差减小小于这个差值，就不用继续划分
    tolN = ops[1]   #划分最小size，小于，就不用继续划分
    if len(set(dataSet[:,-1].T.tolist()[0])) == 1:  #如果集合size为1，不用继续划分
        return None, leafType(dataSet)
    m,n = shape(dataSet)
    S = errType(dataSet)
    bestS = inf; bestIndex = 0; bestValue = 0
    for featIndex in range(n-1):   #对于每个特征
        for splitVal in set(dataSet[:,featIndex]):    #对训练集中该特征每个可能的值
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
            if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN): continue #划分后集合过小，跳过这个值
            newS = errType(mat0) + errType(mat1)
            if newS < bestS:  #如果划分后误差小于bestS，则说明找到新的bestS
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    if (S - bestS) < tolS: #如果最优划分的减小的误差小于tolS，则不划分，产生叶节点
        return None, leafType(dataSet)
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN): #当最佳划分后，集合过小，也不划分，产生叶节点
        return None, leafType(dataSet)
    return bestIndex,bestValue

chooseBestSplit的参数除了dataset，还有，

leafType，产生叶节点的函数

errType，计算误差的函数

对于理解如何定义回归树的leafType和errType

首先如何理解对于数值的树回归，即回归树，我的理解比较像聚类

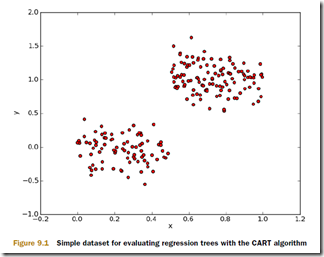
所以，leafType产生叶节点的函数，就是求均值，即用聚类中心点来代表这类数据

而errType，即求这组数据的方差，即希望通过决策树划分，可以让靠近的数据被分到一类中

最后这个参数，ops=(1,4))也非常重要，因为它决定了决策树划分停止的threshold值，被称为预剪枝(prepruning)

之所以这样说，是因为它防止决策树的过拟合，所以当误差的下降值小于tolS，或划分后的集合size小于tolN时，选择停止继续划分

当然问题是，这个算法对于这个参数非常的敏感

比如对于上面的数据集，看上去应该是两个叶节点比较合理，如果ops的值设的过小，会划分出很多叶节点

所以对于决策树算法，很重要的一步是需要解决过拟合问题

常用的方法是用剪枝算法（pruning）

def isTree(obj):
    return (type(obj).__name__=='dict')
def getMean(tree):  #求出tree上所有节点的均值，剪枝就是用均值的叶节点来替换这个子树
    if isTree(tree['right']): tree['right'] = getMean(tree['right'])
    if isTree(tree['left']): tree['left'] = getMean(tree['left'])
    return (tree['left']+tree['right'])/2.0
def prune(tree, testData):
    if shape(testData)[0] == 0: return getMean(tree)
    if (isTree(tree['right']) or isTree(tree['left'])): #存在子树需要递归
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
    if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet)  #递归prune左子树
    if isTree(tree['right']): tree['right'] = prune(tree['right'], rSet)  #递归prune右子树
    if not isTree(tree['left']) and not isTree(tree['right']):   #如果都是叶节点，尝试直接剪枝
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
        errorNoMerge = sum(power(lSet[:,-1] - tree['left'],2)) +\  #计算未剪枝时的error
                       sum(power(rSet[:,-1] - tree['right'],2))
        treeMean = (tree['left']+tree['right'])/2.0
        errorMerge = sum(power(testData[:,-1] - treeMean,2))   #计算剪枝后的error
        if errorMerge < errorNoMerge:   #如果剪枝可以降低error
            print "merging"
            return treeMean  #返回均值来替代子树，达到剪枝的目的
        else: return tree
    else: return tree

思路比较简单，

如果有子树，那么对该子树进行递归剪枝，从叶节点开始，check将叶节点合并，剪枝是否可以降低error，如果可以则合并掉

 

模型树（Model tree）

是回归树的扩展，回归树其实相当于用一个具体的值来拟合一个划分，这个太粗暴了

像之前描述的，我们可以用一个线性模型来拟合一个划分

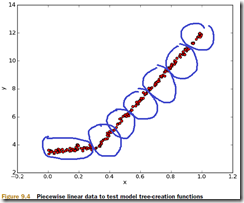
比如对于这样的训练集，如果用简单的回归树去拟合，会拟合出很多的叶节点

而如果用模型树，来拟合，则只会有两个叶节点，每个都是个线性模型，明显更合理，也更容易理解一些

对于模型树，仍然可以直接使用上面的createTree

只不过需要改变一下leafType和errType，

def linearSolve(dataSet): #线性拟合
    m,n = shape(dataSet)
    X = mat(ones((m,n))); Y = mat(ones((m,1)))
    X[:,1:n] = dataSet[:,0:n-1]; Y = dataSet[:,-1]
    xTx = X.T*X
    if linalg.det(xTx) == 0.0:
        raise NameError('This matrix is singular, cannot do inverse,\n\
        try increasing the second value of ops')
    ws = xTx.I * (X.T * Y)
    return ws,X,Y  #返回拟合结果，之所以需要返回X，Y是用于后面计算error

def modelLeaf(dataSet): #叶节点存线性模型的参数ws
    ws,X,Y = linearSolve(dataSet)
    return ws

def modelErr(dataSet):
    ws,X,Y = linearSolve(dataSet)
    yHat = X * ws
    return sum(power(Y - yHat, 2)) #计算预测值和真实值的平方差