【Udacity】数据的差异性：值域、IQR、方差和标准差

一、值域(Range)

Range = Max - Min

受异常值(Outliers)影响

二、四分位差(IQR)

四分位距（interquartile range, IQR），又称四分差。是描述统计学中的一种方法，以确定第三四分位数和第一四分位数的区别（即Q1~Q3 的差距）。

三、异常值(Outlier)

异常值的常用定义：Outlier < Q1 - 1.5IQR

 OR      > Q3 + 1.5IQR

• 可视化——Box Plots(箱线图) & Whisker(盒须图)

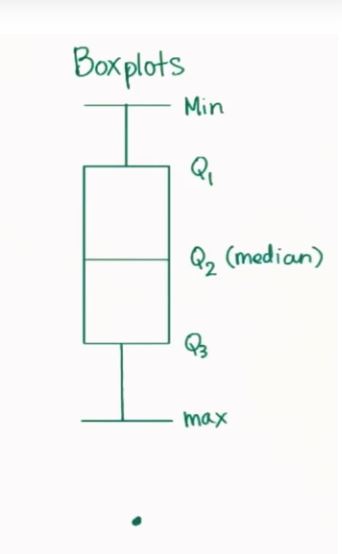
• IQR的不足
  
  值域和IQR都无法将所有数据考虑进来；
  
  完全不同的两个数据集也可以有相同的IQR：Normal(正态分布)、Bimodel(双峰分布)和Uniform distribution(均匀分布)

• we need one number that decribes the spread data that takes all the data into account.(数据分布+考虑所有数据)

四、方差(variance)

• 平均值的平方偏差-Means of squared deviations/average squared deviation

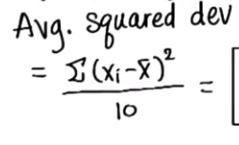
平方和本质——正方形面积

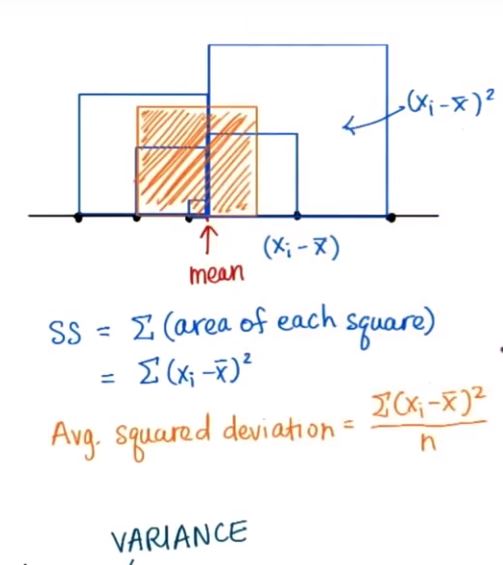
五、标准差(Standard Deviation)

正方形的边长——方差的平方根

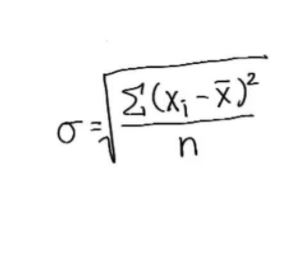
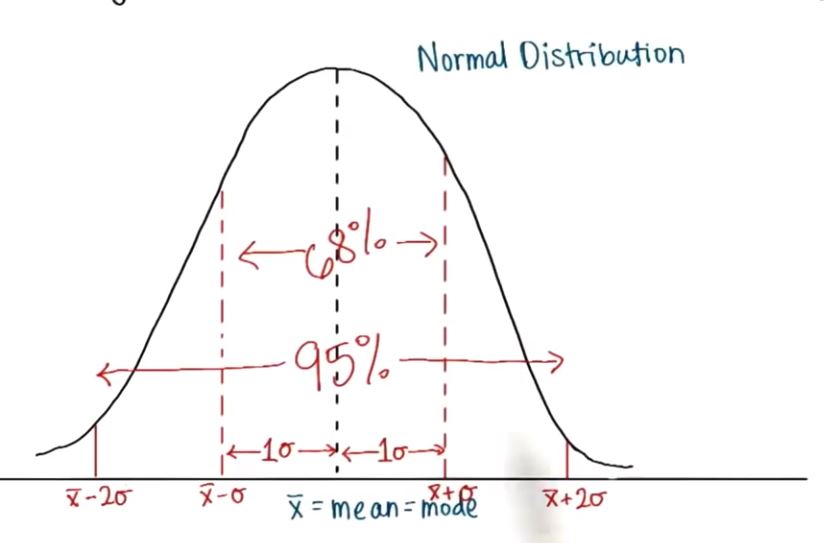
• 标准差和正态分布图

六、贝塞尔校正(Bessel's correction)

• 通常，抽样差异性<总体差异性(遗漏稀有值)
  
  ** n ——> n-1 **

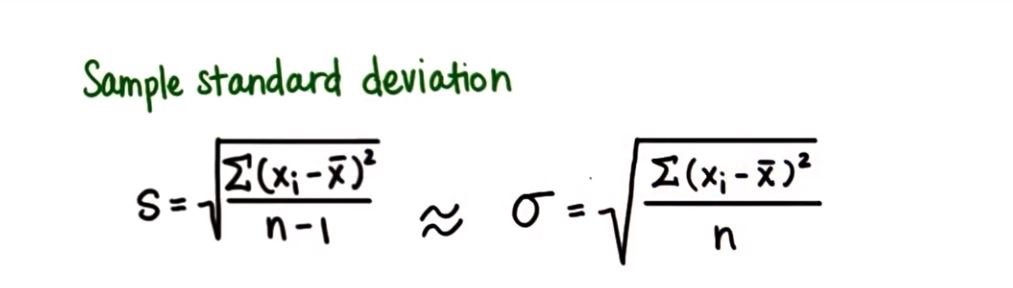
七、样本标准偏差

• 区分总体标准差σ和样本标准差s
  
  1.样本标准差 估算大样本集时使用小写的s
  
  —— 有样本，并需要估算总体标准差——>分母为n-1
  
  —— 有总体数据集——>分母为n