HDU - 6116：路径计数 （组合数&NTT）

一个包含四个点的完全图，可以在任意节点出发，可以在任意节点结束，给出每个点被经过的次数，求有多少种合法的遍历序列。如果两个序列至少有一位是不同的，则认为它们不相同。

Input

2 3 3 3

Sample Output

12336

题意：给a个A，b个B，c个C，d个D，求有少种排列，使得相邻的两个不同。

思路：用容斥来做，ans=所有排列-至少一个相邻+至少两个相邻-...+...。

假设有i堆a，则方案数位C(a-1,i-1)，则a中至少a-i个相邻；同理； 则i堆a，j堆b，k堆c，l堆d，至少有N-i-j-k-l个相邻，其对应的排列数为 N!/(i!*j!*k!*l!)；

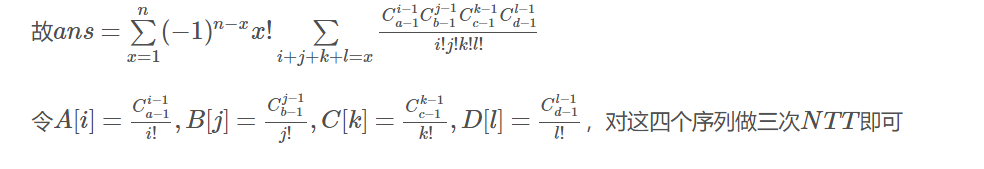
#include<bits/stdc++.h>
#define rep(i,x,y) for(int i=x;i<=y;i++)
using namespace std;
#define MOD Mod
#define ll long long
const int G=;
const int Mod=;
const int maxn=;
int qpow(int v,int p)
{
    int ans=;
    for(;p;p>>=,v=1ll*v*v%Mod)
      if(p&)ans=1ll*ans*v%Mod;
    return ans;
}
void rader(int y[], int len) {
    for(int i=,j=len/;i<len-;i++) {
        if(i<j) swap(y[i],y[j]);
        int k=len/;
        while(j>=k) j-=k,k/=;
        if(j<k) j+=k;
    }
}
void NTT(int y[],int len,int opt) {
    rader(y,len);
    for(int h=;h<=len;h<<=) {
        int wn=qpow(G,(MOD-)/h);
        if(opt==-) wn=qpow(wn,Mod-);
        for(int j=;j<len;j+=h) {
            int w=;
            for(int k=j;k<j+h/;k++) {
                int u=y[k];
                int t=(ll)w*y[k+h/]%MOD;
                y[k]=(u+t)%MOD;
                y[k+h/]=(u-t+MOD)%MOD;
                w=(ll)w*wn%MOD;
            }
        }
    }
    if(opt==-) {
        int t=qpow(len,MOD-);
        for(int i=;i<len;i++) y[i]=(ll)y[i]*t%MOD;
    }
}
int A[maxn],B[maxn],C[maxn],D[maxn],f[maxn],rev[maxn],a,b,c,d;
int main()
{
    int N,K;
    f[]=rev[]=;
    rep(i,,) f[i]=(ll)f[i-]*i%Mod;
    rev[]=qpow(f[],Mod-);
    for(int i=;i>=;i--) rev[i]=(ll)rev[i+]*(i+)%Mod;
    while(~scanf("%d%d%d%d",&a,&b,&c,&d)){
        N=a+b+c+d;
        memset(A,,sizeof(A));
        memset(B,,sizeof(B));
        memset(C,,sizeof(C));
        memset(D,,sizeof(D));
        rep(i,,a) A[i]=(ll)f[a-]*rev[i-]%Mod*rev[a-i]%Mod*rev[i]%Mod;
        rep(i,,b) B[i]=(ll)f[b-]*rev[i-]%Mod*rev[b-i]%Mod*rev[i]%Mod;
        rep(i,,c) C[i]=(ll)f[c-]*rev[i-]%Mod*rev[c-i]%Mod*rev[i]%Mod;
        rep(i,,d) D[i]=(ll)f[d-]*rev[i-]%Mod*rev[d-i]%Mod*rev[i]%Mod;
        int len=; while(len<=N) len<<=;
        NTT(A,len,); NTT(B,len,);
        rep(i,,len-) A[i]=(ll)A[i]*B[i]%Mod;

        NTT(C,len,);
        rep(i,,len-) A[i]=(ll)A[i]*C[i]%Mod;

        NTT(D,len,);
        rep(i,,len-) A[i]=(ll)A[i]*D[i]%Mod;
        NTT(A,len,-);

        int opt,ans=;
        if(N&) opt=; else opt=-;
        rep(i,,N) (((ans+=(ll)opt*f[i]*A[i]%Mod)%=Mod)+=Mod)%=Mod,opt=-opt;
        printf("%d\n",ans);
    }
    return ;
}