LCA问题

基本概念

LCA：树上的最近公共祖先，对于有根树T的两个结点u、v，最近公共祖先LCA(T,u,v)表示一个结点x，满足x是u、v的祖先且x的深度尽可能大。

RMQ：区间最小值查询问题。对于长度为n的数列A，回答若干询问RMQ(A,i,j)，返回数列A中下标在[i,j]里的最小值下标。

朴素LCA算法

求出树上每个结点的深度。

对于查询LCA(u,v)，用p1、p2指向将u、v，将p1、p2中深度较大的结点不断指向其父结点，直到p1、p2深度相同。

之后p1、p2同步向上移动，直到p1=p2，此时p1、p2所指向的结点就是LCA(u,v)。

LCA向RMQ转化

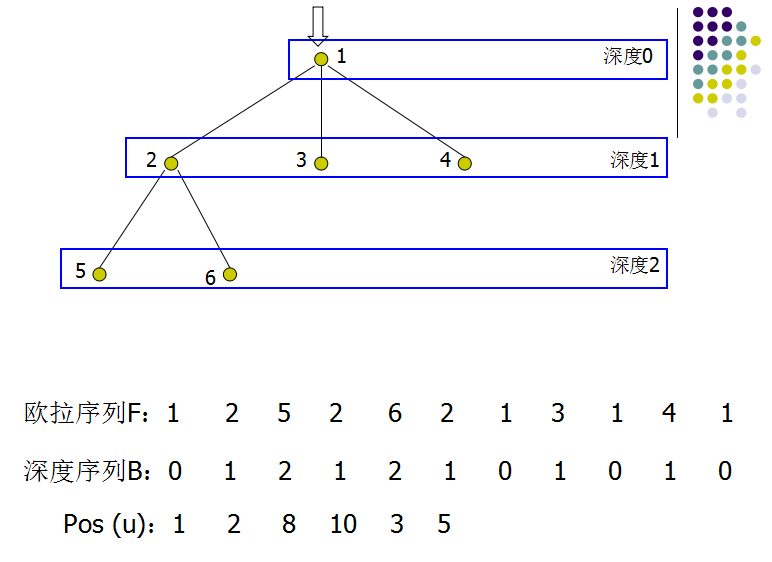
对有根树进行DFS，将遍历到的结点按顺序记录下来，将会得到一个长度为2N-1的序列，称之为T的欧拉序列F。

每个结点都在欧拉序列中出现，记录结点u在欧拉序列中第一次出现的位置为pos[u]。

记录结点u的深度为dep[u]，在深度序列中记录欧拉序列中的结点的深度B[1...2N-1]。

根据DFS的性质，对于两结点u、v，从pos[u]遍历到pos[v]的过程中会经过LCA[u,v]，它的深度是深度序列B[pos[u]...pos[v]]中最小的。

那么求LCA(T,u,v)，就等价于求RMQ(B,u,v)。

LCA的Tarjan算法

解决LCA问题的Tarjan算法利用并查集在一次DFS（深度优先遍历）中完成所有询问。它是时间复杂度为O(N+Q)的离线算法，这里的Q表示查询次数。

算法DFS有根树T，定义从根节点到当前正在遍历的结点u的路径为活跃路径P。

对于每个已经遍历过的结点x，我们使用并查集将其连接到P上距离其最近的结点F(x)。

记录与u有关的询问集合为Q(u)。

对于Q(u)中的任意一组询问LCA(u, v)，如果v已经遍历过，那么答案即为F(v)。

我们只需要维护当前所有以遍历结点的F即可。

代码流程Tarjan_DFS(u)：

1. 创建并查集u
2. 遍历Q(u)中的所有询问(u,v)，如果v已经被标记，则Answer(u,v)=v所在集合的根。
3. 对于u的每一个儿子v，调用Tarjan_DFS(v)。合并u与v所在的集合，设根为u。
4. 标记u。

倍增LCA

与RMQ的ST算法类似，我们令F[i][0]为结点i的第2^k个父结点。

则F[i][0]为i的父结点，令w为i的第2^k-1个父结点即w=F[i][k-1]，那么w的第2^k-1个父结点就是i的第2^k个父结点即F[i][k]=F[w][k-1]。

在查询LCA时，与朴素LCA类似，先将深度较大的结点u提升到与v的深度相同，而这一次我们利用倍增法，一次提升2^k个父结点，加快了算法的效率。

之后，两个结点同时提高2^k(k是使2^k<=dep[u]最大的正整数)。直到u、v到达同一个结点。那么这个结点就是LCA(u,v)。

倍增法的优点在于，除了能求出LCA(u,v)，还可以对树上的路径进行维护。

例如要求出结点u到结点v路径上最大的边权w，我们可以在预处理F[i][k]时，用一个数组maxCost[i][k]记录结点i到它的第2^k个父结点的路径上最大的边权。

那么在查询LCA(u,v)的过程中，求出u、v到公共祖先的路径上的最大边权，即u到v的路径上的最大边权。

 void preprocess(){
     for (int i=;i<=n;i++){
         anc[i][]=fa[i];
         maxCost[i][]=cost[i];
         for (int j=;(<<j)<n;j++) anc[i][j]=-;
     }
     for (int j=;(<<j)<n;j++){
         for (int i=;i<=n;i++){
             if (anc[i][j-]!=-){
                 int a=anc[i][j-];
                 anc[i][j]=anc[a][j-];
                 maxCost[i][j]=max(maxCost[i][j-],maxCost[a][j-]);
             }
         }
     }
 }
 int query(int p,int q){
     int log;
     if (L[p]<L[q]) swap(p,q);
     for (log=;(<<log)<=L[p];log++);log--;
     int ans=-INF;
     for (int i=log;i>=;i--){
         if (L[p]-(<<i)>=L[q]){
             ans=max(ans,maxCost[p][i]);
             p=anc[p][i];
         }
     }
     if (p==q) return ans;
     for (int i=log;i>=;i--){
         if (anc[p][i]!=-&&anc[p][i]!=anc[q][i]){
             ans=max(ans,maxCost[p][i]);
             p=anc[p][i];
             ans=max(ans,maxCost[q][i]);
             q=anc[q][i];
         }
     }
     ans=max(ans,cost[p]);
     ans=max(ans,cost[q]);
     return ans;
 }    

倍增LCA