Erdos-Renyi随机图的生成方式及其特性

1 随机图生成简介

1.1 $G_{np}$和$G_{nm}$

以下是我学习《CS224W：Machine Learning With Graphs》^[1]中随机图生成部分的笔记，部分补充内容参考了随机算法教材^[2]和wiki^[3]。随机图生成算法应用非常广泛，在NetworkX网络数据库中也内置的相关算法。我觉得做图机器学习的童鞋很有必要了解下。

Erdos-Renyi随机图^[4]以两位著名的匈牙利数学家P.Erdős和A. Rényi的名字命名的，是生成随机无向图最简单和常用的方法，包括以下两种紧密相关的变体：

$G_{np}$: 拥有$n$个节点，且边$(u, v)$以独立同分布的概率$p$产生的无向图
$G_{nm}$: 拥有$n$个节点，且其中$m$条边按照均匀分布采样生成的无向图。

(八卦：最常被讨论的$G_{np}$其实是Gilbert^[5]提出的，不过由于P.Erdős和A. Rényi提出的$G_{nm}$更早一些，后来就将两种都统称Erdos-Renyi随机图了)

1.2 生成方法

$G_{np}$：按某个次序考虑$\tbinom{n}{2}$条可能边中的每一条，然后以概率$p$独立地往图上添加每条边。
$G_{nm}$: 均匀选取$\tbinom{n}{2}$条可能边中的一条，并将其添加为图的边，然后再独立且均匀随机地选取剩余$\tbinom{n}{2}-1$可能边中的一条，并将其添加到图中，直到$m$边为止（可以证明，虽然是无放回采样，但是每次采样是独立的，任意一种$m$条边的选择结果是等概率的）。

值得一提的是，在$G_{np}$中，一个有$n$个顶点的图具有$m$条边的概率满足分布：

\[\tbinom{\tbinom{n}{2}}{m} p^m(1-p)^{\tbinom{n}{2}-m}
\]

该分布式二项分布，边的期望数为$\tbinom{n}{2}p$，每个顶点度的期望为$(n-1)p$。

1.3 两种方法比较

两者的相同点：节点数量都为$n$，且边数量的期望为$p\tbinom{n}{2}$；
两者的区别：$G_{np}$的可能边数量在$\tbinom{n}{2}p$上下波动，而$G_{nm}$则恒定有$m$条边。

2 $G_{np}$随机图

2.1 只用$n$和$p$够吗？

$n$和$p$并不能完全决定一个图。我们发现即使给定$n$和$p$，图也有许多实现形式。如当$n=10, p=1/6$时，就可能产生如下的图：

2.2 $G_{np}$的图属性

接下来我们考虑给定$n$和$p$，图$G_{np}$所可能拥有的不属性，包括度分布$p(k)$、聚类系数$C$、连通分量、平均最短路径长度$\bar{h}$等。

度分布

$G_{np}$的度分布是满足二项分布的，我们设$p(k)$为任意节点度数的概率分布函数。当节点数$n$足够大时，$p(k)$可视为对度为$k$的节点所占比例的近似。我们有：

\[p(k)=\left(\begin{array}{c}
n-1 \\
k
\end{array}\right) p^{k}(1-p)^{n-1-k}\quad (k=0, 1,..., n-1)
\]

其中$\left(\begin{array}{c}
n-1 \\
k
\end{array}\right)$表示从$n-1$个节点中选$k$个节点，$p$为边产生的概率。该分布是二项分布，所以我们有以下均值和方差：

\[\begin{aligned}
& \bar{k} =(n-1)p \\
& \sigma^2 = (n-1)p(1-p)
\end{aligned}
\]

二项分布的离散分布图像如下图所示：

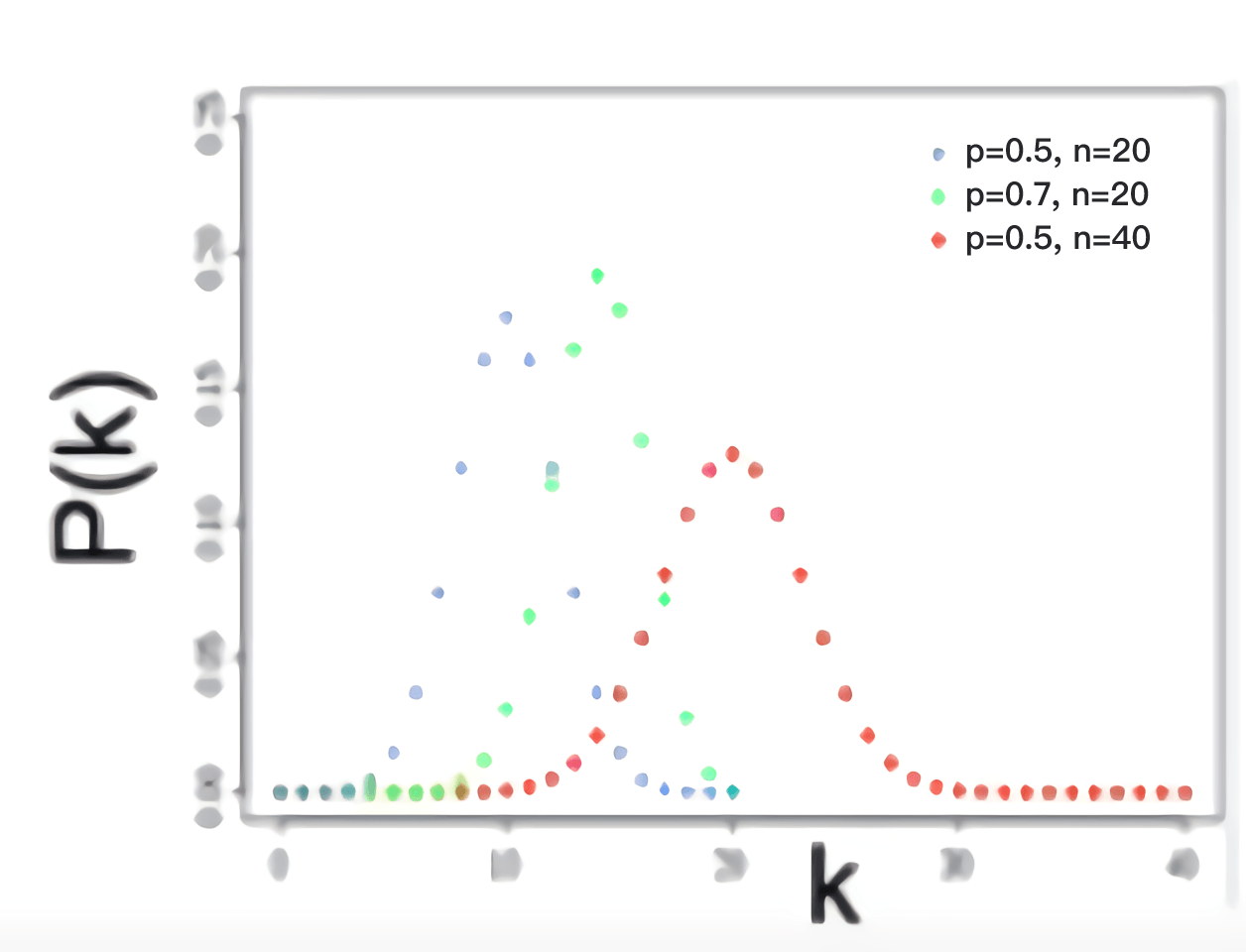
当$n$足够大时，二项分布可以用正态分布去近似。

聚类系数

我们设

\[C_{i}=\frac{e_{i}}{\tbinom{k_i}{2}}
\]

此处$e_i$为节点$i$邻居之间的边数，$k_i$为节点$i$的度，$\tbinom{k_i}{2}$为节点$i$的邻居间可能存在的边总数。由于$G_{np}$中边都按照概率$p$独立同分布，我们有

\[\mathrm{E}(e_i)= \tbinom{k_i}{2}p
\]

其中$p$为节点$i$的邻居间两两结合的概率，$\tbinom{k_i}{2}$为节点$i$的邻居间可能存在的边总数。

我们进一步可推知聚类系数：

\[C =\mathrm{E}(C_i)= \frac{\mathrm{E}(e_i)}{\tbinom{k_i}{2}}=p=\frac{\bar{k}}{n-1} \approx \frac{\bar{k}}{n}
\]

连通分量

图$G_{np}$的图结构会随着$p$变化，如下图所示：

观察可知其中当巨大连通分量（gaint connected component）出现时，$p = 1/(n-1)$，此时平均度$\bar{k} = (n-1)p=1$。

平均度$k=1-\varepsilon$(即小于1)时，所有的连通分量大小为$\Omega(\log n)$；

平均度$k = 1 + \varepsilon$（即高于1）时，存在一个连通分量大小为$\Omega(n)$，其它的大小为$\Omega(\log n)$。且每个节点在期望值上至少有一条边。

如下图所示为$G_{np}$中，$n=100000$，$\bar{k}=(n-1)p=0.5,..., 3$ 时的模拟实验图像：

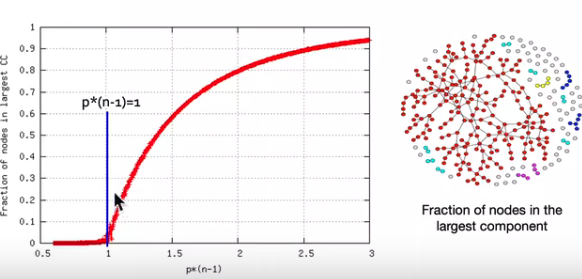
根据模拟实验，在$G_{np}$中，平均度大于1时，巨大连通分量恰好出现。

平均最短路径长度

Erdos-Renyi随机图即使扩展到很大，仍然可以保证节点之间只有几跳(hops)的距离，如下所示为图的平均最短路径长度$\bar{h}$随节点数量变化的关系图：

可以看到平均最短路径长度$\bar{h}$随着节点数量$n$增长并满足$O(\log n)$的增长阶。

2.3 真实网络和$G_{np}$的对比

相似点：存在大的连通分量，平均最短路径长度

不同点：聚类系数，度分布

在实际应用中，随机图模型可能有以下问题：

度分布可能和真实网络不同，毕竟真实网络不是随机的。
真实网络中巨大连通分量的出现可能不具有规律性。
可能不存在局部的聚类结构，以致聚类系数太小。

3 代码库

NetworkX中内置了Erdos-Renyi随机图的生成函数，包括$G_{np}$和$G_{nm}$。就是需要注意$G_{np}$的API^[6]是

erdos_renyi_graph(n, p, seed=None, directed=False)

该API与nx.binomial_graph 、nx.gnp_random_graph作用是相同的。

而$G_{nm}$的API^[7]是

nm_random_graph(n, m, seed=seed, directed=False)

故大家在实际使用中要注意区分。

参考

[1] http://web.stanford.edu/class/cs224w/
[2]

Mitzenmacher M, Upfal E. Probability and computing: Randomization and probabilistic techniques in algorithms and data analysis[M]. Cambridge university press, 2017.
[3] https://zh.m.wikipedia.org/zh-hans/随机图
[4]

Erdős P, Rényi A. On the evolution of random graphs[J]. Publ. Math. Inst. Hung. Acad. Sci, 1960, 5(1): 17-60.
[5]

Gilbert E N. Random graphs[J]. The Annals of Mathematical Statistics, 1959, 30(4): 1141-1144.
[6] https://networkx.org/documentation/stable/reference/generated/networkx.generators.random_graphs.erdos_renyi_graph.html
[7] https://networkx.org/documentation/stable/auto_examples/graph/plot_erdos_renyi.html?highlight=renyi