【GLSL教程】（九）其他说明 【转】

http://blog.csdn.net/racehorse/article/details/6664775

法线矩阵
在很多顶点shader中都用到了gl_NormalMatrix。这里将介绍这个矩阵是什么，以及它的作用。
大部分计算是在视图空间内完成的，主要原因是光照的运算要放在这个空间内，否则一些依赖观察点坐标的效果，比如镜面反射光就很难实现。
所以我们需要将法线变换到视图空间。变换一个顶点到视图空间的方法如下：

1. vertexEyeSpace = gl_ModelViewMatrix * gl_Vertex;

对法线也能如此操作吗？一个法线是3个浮点数组成的向量，而模型视图矩阵是一个4×4的矩阵。另外，因为法线是一个向量，我们只需要变换它的方向，而模型视图矩阵中左上方的3×3子矩阵正好包含了旋转变换。所以可不可以用法线来乘这个子矩阵呢？
下面的代码很简单地实现了这个要求：

1. normalEyeSpace = vec3(gl_ModelViewMatrix * vec4(gl_Normal,0.0));

这样的话，gl_NormalMatrix还有什么用呢？只是为了简化代码书写吗？实际当然不是这么简单，上面的代码在某些情况下是有效的，但不能应对所有情况。
让我们看看潜在的问题：

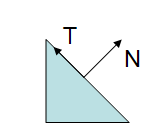
在上图中我们可以看到一个三角面以及它的法线和切线。下图显示了如果模型视图矩阵包含非一致缩放（non-uniform scale）的话会发生什么。

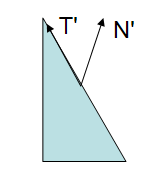
注意，如果缩放是一致的（uniform），那么法线方向保持不变，变的只是长度，而且可以通过归一化修正这个影响。
在上图中，模型视图矩阵应用到所有顶点以及法线上，最后的结果明显错误：法线不再与三角面垂直了。
现在我们知道模型视图矩阵在某些情况下，不能用来变换法线向量。下面的问题就是：那么该使用哪个矩阵？
考虑一个3×3矩阵G，让我们看看要正确变换法线，这个矩阵该是什么样子。
我们知道，变换前切线和法线是垂直的，即T•N = 0，在变换后切线和法线同样应该保持垂直，即T’•N’ =
0。现在假设G是正确变换法线的矩阵，同时模型视图矩阵的左上3×3子矩阵M可以正确变换切线T（T是一个向量，所以w成分为0）。因为T可以通过两个顶
点的差来计算，所以变换顶点的矩阵同样可以用来变换T。由此可以得到如下等式：

向量的点乘相当于向量的内积，所以有：

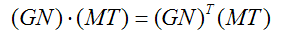
我们知道相乘的转置等于分别转置再交换顺序相乘：

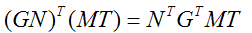
已知N和T点乘结果为0，所以如果下式成立就可以满足等式为0：

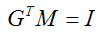
即有：

可见变换法线的正确矩阵是M的逆的转置。OpenGL计算出的这个矩阵就保存在gl_NormalMatrix里。
在本节开始讨论过，某些情况下使用模型视图矩阵也可以。当模型视图矩阵的左上3×3子矩阵M正交时，可以得到：

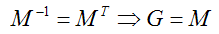
一个正交矩阵的所有行/列都为单位向量，并且互相正交。当两个向量乘上正交矩阵时，它们之间的夹角在变换前后不变。由于这种保角变换的关系，所以法线和切线依然保存垂直。此外，向量的长度也保持不变。
M在什么时候能确定为正交的呢？当我们把几何变换限制为旋转和平移时（在OpenGL应用程序中只使用glRotate和glTranslate，而不使用glScale），就可以保证M正交。注意：gluLookAt同样建立正交矩阵。

关于法线归一化
当一个法线到达顶点shader后，我们一般会将它归一化：

1. normal = normalize(gl_NormalMatrix * gl_Normal);

法线与gl_NormalMatrix矩阵相乘，将会被变换到视图空间。归一化向量可以保证使用点乘得到余弦值。
我们可以避免归一化计算吗？在某些情况下是可行的。如果gl_NormalMatrix是正交矩阵，那么经过变换后输入法线的长度不会变，依然等于gl_Normal。所以如果在OpenGL程序中法线已经是归一化的，那么在shader中就不需要在重复了。
也就是说，如果我们使用gluLookAt设置照相机，对模型值进行旋转和平移变换，就可以在shader中避免使用归一化操作。这对于归一化过的光线向量也是适用的。
片断shader的情况
在片断shader中，我们经常发现需要重新归一化在顶点shader中归一化的法线。这是必要的吗？答案是肯定的。
考虑一个包含三个不同顶点法线的三角面。片断shader接收经过插值的法线，插值基于距离三个顶点的远近。这样得到的法线方向是对的，但不再是单位长度了。
下图显示了原因。图中黑线表示三角面，顶点法线用蓝色表示，插值得到的片断法线用绿色表示。所有的插值法线排列在黑色的点划线上。从图上可以看出绿色的插值法线大小小于单位长度的顶点法线。

注意，如果顶点法线没有单位化，那么得到的插值法线的方向也将是错误的。所以，即使一个顶点没有在顶点shader用到，也可能要对它在顶点shader中进行归一化。
有一种情况，在片断shader中可以避免归一化操作，那就是每个顶点法线方向相同，而且顶点法线是经过归一化的。此时顶点法线插值得到的结果都相同。
以方向光为例，每个片断都需要考虑光线方向，如果光线向量已经在之前归一化了，在片断shader中就可以避免归一化这一步。