洛谷 P1228 【地毯填补问题】

事实上感觉四个的形状分别是这样:

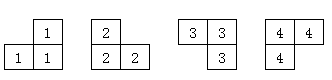
spj报错：

1:c 越界

2:x,y 越界

3:mp[x][y] 已被占用

4:mp[x][y] 从未被使用

题解：

初看这个问题，似乎无从下手，于是我们可以先考虑最简单的情况，既n = 2时

0 0 0 1 这时，无论公主在哪个格子，我们都可以用一块毯子填满

继续考虑n = 4的情况

我们已经知道了解决2 * 2的格子中有一个障碍的情况如何解决，因此我们可以尝试构造这种情况

首先，显然可以将4 4的盘面划分成4个2 2的小盘面，其中一块已经存在一个障碍了

而我们只需在正中间的2 * 2方格中放入一块地毯，就可以使所有小盘面都有一个障碍

于是，n = 4的情况就解决了

我们可以将n = 4时的解法可以推广到一般情况，既当n = 2 k时，我们均可以将问题划分为4个n = 2 k – 1的子问题，然后分治解决即可。

下面附上代码（算法：分治）：

#include<cstdio>
typedef long long ll;
ll x,y,len; int k;
ll fun(int k)
{
    ll sum=1;
    for(int i=1;i<=k;++i) sum*=2;
    return sum;
}
void solve(ll x,ll y,ll a,ll b,ll l)
{
    if(l==1) return;
    if(x-a<=l/2-1 && y-b<=l/2-1)
    {
        printf("%lld %lld 1\n",a+l/2,b+l/2);
        solve(x,y,a,b,l/2);
        solve(a+l/2-1,b+l/2,a,b+l/2,l/2);
        solve(a+l/2,b+l/2-1,a+l/2,b,l/2);
        solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);
    }
    else if(x-a<=l/2-1 && y-b>l/2-1)
    {
        printf("%lld %lld 2\n",a+l/2,b+l/2-1);
        solve(a+l/2-1,b+l/2-1,a,b,l/2);
        solve(x,y,a,b+l/2,l/2);
        solve(a+l/2,b+l/2-1,a+l/2,b,l/2);
        solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);
    }
    else if(x-a>l/2-1 && y-b<=l/2-1)
    {
        printf("%lld %lld 3\n",a+l/2-1,b+l/2);
        solve(a+l/2-1,b+l/2-1,a,b,l/2);
        solve(a+l/2-1,b+l/2,a,b+l/2,l/2);
        solve(x,y,a+l/2,b,l/2);
        solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);
    }
    else
    {
        printf("%lld %lld 4\n",a+l/2-1,b+l/2-1);
        solve(a+l/2-1,b+l/2-1,a,b,l/2);
        solve(a+l/2-1,b+l/2,a,b+l/2,l/2);
        solve(a+l/2,b+l/2-1,a+l/2,b,l/2);
        solve(x,y,a+l/2,b+l/2,l/2);
    }
}
int main()
{
    scanf("%d %lld %lld",&k,&x,&y);
    len=fun(k);
    solve(x,y,1,1,len);
    return 0;
}