openjudge-膨胀的木棍
http://noi.openjudge.cn/ch0111/09/
- 总时间限制: 1000ms 内存限制: 65536kB
- 描述
-
当长度为L的一根细木棍的温度升高n度,它会膨胀到新的长度L'=(1+n*C)*L,其中C是热膨胀系数。
当一根细木棍被嵌在两堵墙之间被加热,它将膨胀形成弓形的弧,而这个弓形的弦恰好是未加热前木棍的原始位置。
你的任务是计算木棍中心的偏移距离。
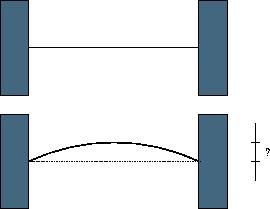
输入
三个非负实数:木棍初始长度(单位:毫米),温度变化(单位:度),以及材料的热膨胀系数。
保证木棍不会膨胀到超过原始长度的1.5倍。
输出
木棍中心的偏移距离(单位:毫米),保留到小数点后第三位。
样例输入
1000 100 0.0001
样例输出
61.329
参考:
http://blog.csdn.net/jeremygjy/article/details/49686943
http://blog.csdn.net/txl199106/article/details/49332261
#include<stdio.h>
#include<math.h>
#define PI (acos(-1))
#define eps (1e-14)
int main(int argc, char *argv[])
{
double L,n,C,L1; double minCentralAngle,maxCentralAngle,CentralAngle;
double radius,L2;
double ans; scanf("%lf%lf%lf",&L,&n,&C); if(n*C*L<=eps) //假如膨胀量太小就不用计算了,直接认为结果就是0.
{
printf("0.000\n");
return ;
} L1=(+n*C)*L; //下面对圆心角进行二分枚举
//(膨胀量不超过原来的1.5倍,
//分析圆的半周长PI*R与直径2*R的关系可知圆心角范围0~2*PI而且不可能取2*PI)
minCentralAngle=;//圆心角的极小值
maxCentralAngle=PI;//圆心角的极大值
while(minCentralAngle<maxCentralAngle-eps)
{
CentralAngle=(minCentralAngle+maxCentralAngle)/;
radius=L//sin(CentralAngle/);
L2=CentralAngle*radius;
if(L2>=L1)//当弦长固定时,圆心角越大 ,弧长就越大
maxCentralAngle=CentralAngle;
else if(L2<L1)
minCentralAngle=CentralAngle;
}
radius=L//sin(minCentralAngle/);
ans=radius-L//tan(minCentralAngle/);
printf("%.3lf\n",ans);
return ;
}
一定要注意:我们需要二分的内容是当前角度,那么角度的范围可以很容易发现,因为木棍长度不超过1.5倍那么就定角度为0-π因为如果圆心角过小会发现半径十分的大根本存不下,其实这种情况的时候木棍长度的变化也是十分的小的那么
if(n * c * L <= eps)
判断一下如果满足那么直接就输出0.000,
另外要注意:当弦长固定时,圆心角越大 ,弧长就越大 。
网友JeremyGJY的代码和分析很好,摘抄一下:

JeremyGJY的代码:
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const double PI = asin(1.0);
const double eps = 1e-;
int main(){
double Len1, Len2, Temp, ks;
while(scanf("%lf%lf%lf", &Len1, &Temp, &ks) != EOF){
Len2 = (1.0 + Temp * ks) * Len1;
double l=, r=PI;
if(Temp * ks * Len1 <= eps){
printf("%.3lf\n", 0.0);
continue;
}
while(l < r - eps){
double mid = (l + r)/2.0;
if(Len1/sin(mid)*PI*(mid/PI) >= Len2)
r = mid;
else l = mid;
}
printf("%.3lf\n", Len1//sin(l)-Len1//sin(l)*cos(l));
} return ;
}
csdn网友Tank_long的分析更精彩,只不过下面这个图的公式似乎有点乱。
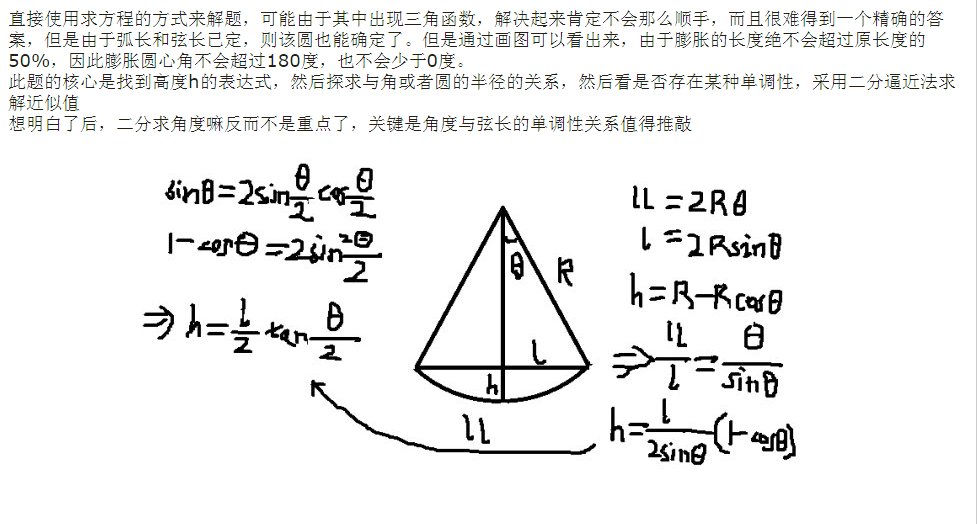
公式大概如下:
首先要注意θ角是圆心角的一半。然后根据数学公式有:
sinθ=2sin(θ/2)cos(θ/2)
1-cosθ=2sin(θ/2)2
然后还要注意根据直角三角形正弦的定义有:L=2*R*sinθ
根据弧长公式有LL=2*R*θ
所以h=R-R*cosθ=R*(1-cosθ)=L/(2*sinθ)*(1-cosθ)=L/(2*sinθ)*(2sin(θ/2)2)=L/( 2* ( 2*sin(θ/2)*cos(θ/2) ) )*(2sin(θ/2)2 )
最后h=L/2*tan(θ/2)
注意到θ是圆心角的一半,所以θ得区间是0~PI,根据正切函数图形性质可以知道当L固定时,h跟θ是成正比关系的。
Tank_long的代码:(不得不佩服起数学功底啊……)
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main()
{
double l, ll, rig, lef, mid, n, c;
scanf("%lf%lf%lf", &l, &n, &c); if(l<1e-)
{
printf("0.000\n");
return ;
}
ll=l*(+n*c);
lef=0.0; //角的极小值
rig=asin(1.0); //角的极大值
//由于三角函数转换,得到 h= (l/2)*tan(@/2) , 所以h只与角@有关,使用二分逼近法去求解最接近的@即可
//注意,二分验证是让 ll与角@ 计算得到的 木棍原始长度l`=ll*sin@/@ 与 l 进行比较,且l`与@成反比例关系
while(rig-lef>1e-) //在极大值与极小值之间进行二分,这个地方精度控制太低就过不了了。精度要求很高。
{
mid=(rig+lef)/;
if(ll*sin(mid)/mid<=l)
rig=mid;
else
lef=mid;
}
printf("%.3lf\n", l/*tan(lef/));
return ;
}
三角函数公式补充:
二倍角公式
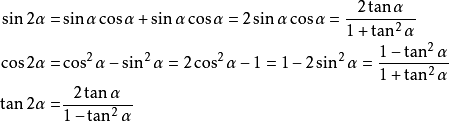
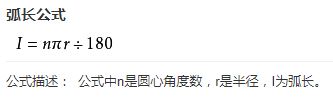
openjudge-膨胀的木棍的更多相关文章
- 二分 题目 压缩打包 Special Judge? 不不不 当然不是
http://noi.openjudge.cn/ch0111/ No 题目 分数 01 查找最接近的元素 10 3176 02 二分法求函数的零点 10 2181 03 矩形分割 10 1420 04 ...
- 【noiOJ】p7939
09:膨胀的木棍 查看 提交 统计 提问 总时间限制: 1000ms 内存限制: 65536kB 描述 当长度为L的一根细木棍的温度升高n度,它会膨胀到新的长度L'=(1+n*C)*L,其中C是热 ...
- POJ 1905 Expanding Rods 木棍膨胀
描述 当长度为L的一根细木棍的温度升高n度,它会膨胀到新的长度L'=(1+n*C)*L,其中C是热膨胀系数. 当一根细木棍被嵌在两堵墙之间被加热,它将膨胀形成弓形的弧,而这个弓形的弦恰好是未加热前木棍 ...
- OpenJudge 2817:木棒 / Poj 1011 Sticks
1.链接地址: http://bailian.openjudge.cn/practice/2817/ http://poj.org/problem?id=1011 2.题目: 总时间限制: 1000m ...
- BZOJ 1044 木棍分割 解题报告(二分+DP)
来到机房刷了一道水(bian’tai)题.题目思想非常简单易懂(我的做法实际上参考了Evensgn 范学长,在此多谢范学长了) 题目摆上: 1044: [HAOI2008]木棍分割 Time Limi ...
- 【OpenJudge 8463】Stupid cat & Doge
http://noi.openjudge.cn/ch0204/8463/ 挺恶心的一道简单分治. 一开始准备非递归. 大if判断,后来发现代码量过长,决定大打表判断后继情况,后来发现序号不对称. 最后 ...
- 【OpenJudge 191】【POJ 1189】钉子和小球
http://noi.openjudge.cn/ch0405/191/ http://poj.org/problem?id=1189 一开始忘了\(2^{50}\)没超long long差点写高精度Q ...
- 【OpenJudge 1665】完美覆盖
http://noi.openjudge.cn/ch0405/1665/?lang=zh_CN 状压水题,手动转移 #include<cstdio> #include<cstring ...
- 【OpenJudge 1793】矩形覆盖
http://noi.openjudge.cn/ch0405/1793/ 好虐的一道题啊. 看数据范围,一眼状压,然后调了好长时间QwQ 很容易想到覆盖的点数作为状态,我用状态i表示至少覆盖状态i表示 ...
随机推荐
- swift 闭包循环引用
当使用闭包时,类本身持有self,然后又在闭包中访问了self或者self的属性,就会导致恶心额循环引用.swift提供的解决方法是在闭包中定义捕获列表,捕获列表是闭包想怎么引用捕获来的变量.例如下面 ...
- oracle 11g dmp文件导入10g
需要导表的时候死活进不去, 现在没需求了.试了一把,一点问题都没.无语.下次遇到问题解决下吧. 导入导出命令:imp abc/abc123@ORCL file='d:\脚本\new\t_adverti ...
- mysql 分组查询问题 group_concat
这几天在做购物车的时候.购物车内的商品为一个商品占一行,结果再从数据库读出的时候,没有分组,而是循环所有的内容出来,然后进行判断.如果一样的话就把他保存到一个变量中.但是自己逻辑没搞清楚.一直出bug ...
- SqlServer类库(自定义)
1,引用System.Configuration; 2,新建应用程序配置文件 读取SqlDataReader中的数据用where (read.Read()){//DoSomeThings()}
- angular 滚动
AngularJs $anchorScroll.$controller.$document $anchorScroll 根据HTML5的规则,当调用这个函数时,它检查当前的url的hash值并且滚动到 ...
- Unity使用protobuf-net进行二进制序列化与反序列化
Protobuf-net提供的一种易于使用的数据序列化方案,可序列化带有[ProtoContract]特性的类实例,并可支持Unity各个发布平台,且效率高.易用性强. public static c ...
- github提交代码流程:
(1) 检查一遍代码改动 $git status (2) 将工作目录中的代码提交到暂存区 $ git add filename git add -A (3) 提交代码到本 ...
- codeforces 724D(贪心)
题目链接:http://codeforces.com/contest/724/problem/D 题意:给定一个字符串和一个数字m,选取一个一个子序列s,使得对于字符串中任意长度为m的子序列都至少含有 ...
- iOS学习之iOS沙盒(sandbox)机制和文件操作之NSFileManager(三)
1.在Documents里创建目录 创建一个叫test的目录,先找到Documents的目录, NSArray *paths = NSSearchPathForDirectoriesInDomains ...
- Array(数组)--map方法
关于Array.prototype.map() MDN 给的定义是: 在作用数组元素的每一项上调用一个方法(callback),返回一个新数组: 使用格式:arr.map(callback[,this ...
