一步一步写数据结构(二叉树的建立和遍历,c++)
简述:
二叉树是十分重要的数据结构,主要用来存放数据,并且方便查找等操作,在很多地方有广泛的应用。
二叉树有很多种类,比如线索二叉树,二叉排序树,平衡二叉树等,本文写的是最基础最简单的二叉树。
思路:
二叉树的建立采用的是递归的思想:给定一个指向根节点的指针,然后递归调用ceate()函数,自动生成一个二叉树。就像是在地上挖了个坑(根节点),然后他会拿着铲子(create函数)按照一定的规则自动挖一个很大的洞穴(二叉树)出来。当然挖坑前需要先定义每个洞长什么样(定义节点结构)。
二叉树的遍历采用的也是递归的思想:如果节点有数据,则按照遍历规则打印根节点和孩子节点,没有数据则返回直到所有数据都遍历完,递归结束。
不废话,上代码:
#include<iostream>
using namespace std; //定义节点
typedef struct node
{
struct node *lchild;
struct node *rchild;
char data;
}BiTreeNode, *BiTree; //*BiTree的意思是给 struct node*起了个别名,叫BiTree,故BiTree为指向节点的指针。 //按照前序顺序建立二叉树
void createBiTree(BiTree &T) //&的意思是传进来节点指针的引用,括号内等价于 BiTreeNode* &T,目的是让传递进来的指针发生改变
{
char c;
cin >> c;
if('#' == c) //当遇到#时,令树的根节点为NULL,从而结束该分支的递归
T = NULL;
else
{
T = new BiTreeNode;
T->data=c;
createBiTree(T->lchild);
createBiTree(T->rchild);
}
} //前序遍历二叉树并打印
void preTraverse(BiTree T)
{
if(T)
{
cout<<T->data<<" ";
preTraverse(T->lchild);
preTraverse(T->rchild);
}
}
//中序遍历二叉树并打印
void midTraverse(BiTree T)
{
if(T)
{
midTraverse(T->lchild);
cout<<T->data<<" ";
midTraverse(T->rchild);
}
}
//后续遍历二叉树并打印
void postTraverse(BiTree T)
{
if(T)
{
postTraverse(T->lchild);
postTraverse(T->rchild);
cout<<T->data<<" ";
}
}
int main()
{
BiTree T; //声明一个指向二叉树根节点的指针
createBiTree(T);
cout<<"二叉树创建完成!"<<endl;
cout<<"前序遍历二叉树:"<<endl;
preTraverse(T);
cout<<endl;
cout<<"中序遍历二叉树:"<<endl;
midTraverse(T);
cout<<endl;
cout<<"后序遍历二叉树:"<<endl;
postTraverse(T);
return ;
}
测试结果:
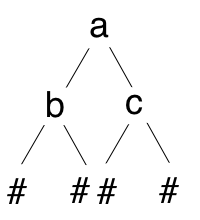
假设我们要建立一个如下图所示的二叉树,#代表空节点,按照前序遍历顺序二叉树表示为:ab##c##
. 
下面是代码的运行结果,正如预期:
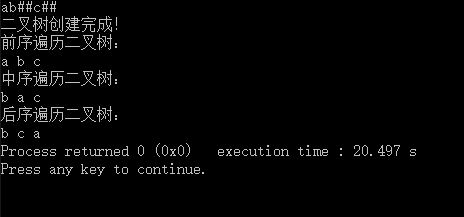
一步一步写数据结构(二叉树的建立和遍历,c++)的更多相关文章
- C语言二叉树的建立与遍历
二叉树的建立和遍历都要用到递归,先暂时保存一下代码,其中主要是理解递归的思想,其它的就都好理解了.这里是三种遍历方式,其实理解一种,其它的几个就都理解了,就是打印出来的顺序不一样而已.建立和遍历的方式 ...
- 二叉树的建立以及遍历的多种实现(python版)
二叉树是很重要的数据结构,在面试还是日常开发中都是很重要的角色. 首先是建立树的过程,对比C或是C++的实现来讲,其涉及到了较为复杂的指针操作,但是在面向对象的语言中,就不需要考虑指针, 内存等.首先 ...
- 二叉树的建立与遍历(c语言)入门
树其实在本质上就是一对多,链表就是一对一. 二叉树的建立: 这里的代码采用的是最粗暴的创建方法,无实际用处.但初次学习二叉树可以通过这个创建方法更好的理解二叉树. 二叉树的遍历: 遍历在大体上分为递归 ...
- C语言实现二叉树的建立、遍历以及表达式的计算
实现代码 #include <stdio.h> #include <stdlib.h> #include <malloc.h> #include <ctype ...
- 二叉树的建立与遍历(山东理工OJ)
题目描写叙述 已知一个按先序序列输入的字符序列,如abc,,de,g,,f,,,(当中逗号表示空节点).请建立二叉树并按中序和后序方式遍历二叉树,最后求出叶子节点个数和二叉树深度. 输入 输入一个长度 ...
- python实现二叉树的建立以及遍历(递归前序、中序、后序遍历,队栈前序、中序、后序、层次遍历)
#-*- coding:utf-8 -*- class Node: def __init__(self,data): self.data=data self.lchild=None self.rchi ...
- 一步一步写平衡二叉树(AVL树)
平衡二叉树(Balanced Binary Tree)是二叉查找树的一个进化体,也是第一个引入平衡概念的二叉树.1962年,G.M. Adelson-Velsky 和 E.M. Landis发明了这棵 ...
- 一步一步写算法(之prim算法 下)
原文:一步一步写算法(之prim算法 下) [ 声明:版权所有,欢迎转载,请勿用于商业用途. 联系信箱:feixiaoxing @163.com] 前两篇博客我们讨论了prim最小生成树的算法,熟悉 ...
- 一步一步写算法(之prim算法 上)
原文:一步一步写算法(之prim算法 上) [ 声明:版权所有,欢迎转载,请勿用于商业用途. 联系信箱:feixiaoxing @163.com] 前面我们讨论了图的创建.添加.删除和保存等问题.今 ...
随机推荐
- Database学习 - mysql 数据库 事务操作
事务 事务指逻辑上的一组操作,组成这组操作的各个单元,要不全部成功,要不全部不成功. 数据库开启事务命令: start transaction 开启事务 rollback 回滚事务,即撤销指定的 ...
- Androidstudio中jar包重复或jar包里的类重复问题
https://www.jianshu.com/p/dd5d4fda1df8 http://blog.csdn.net/hqb112233/article/details/51514208
- 函数前加static与不加static的区别
1:加了static后表示该函数失去了全局可见性,只在该函数所在的文件作用域内可见 2:当函数声明为static以后,编译器在该目标编译单元内只含有该函数的入口地址,没有函数名,其它编译单元便不能通过 ...
- numpy中 array数组的shape属性
numpy.array 的shape属性理解 在码最邻近算法(K-Nearest Neighbor)的过程中,发现示例使用了numpy的array数组管理,其中关于array数组的shape(状态)属 ...
- 恶意PDF文档分析记录
0x1 PDF是什么 PDF(便携式文件格式,Portable Document Format)是由Adobe Systems在1993年用於文件交换所发展出的文件格式. 因为PDF的文件格式性质广泛 ...
- DMA内存申请--dma_alloc_coherent 及 寄存器与内存【转】
转自:https://blog.csdn.net/ic_soc_arm_robin/article/details/8203933 在项目驱动过程中会经常用到dma传输数据,而dma需要的内存有自己的 ...
- Async 详解
一:流程控制 为了适应异步编程,减少回调的嵌套,我尝试了很多库.最终觉得还是async最靠谱. 地址:https://github.com/caolan/async Async的内容分为三部分: 流程 ...
- 转载:2.2.2 配置项的语法格式《深入理解Nginx》(陶辉)
原文:https://book.2cto.com/201304/19627.html 从上文的示例可以看出,最基本的配置项语法格式如下: 配置项名 配置项值1 配置项值2 - ; 下面解释一下配置项的 ...
- Spring整合strus2简单应用总结
本身strus2没接触过,所以这块学的一知半解,正常不整合的还没学(接着学) step: 1.创建web工程 2.在/WEB-INF/lib引入jar包 asm-3.3.jarasm-commons- ...
- Nodejs实现WebSocket通信demo
一.创建websocket.js文件 步骤: 1.创建websocket.js文件,复制如下代码: 2.安装nodejs-websocket依赖: 3.该文件夹下命令行执行 node websocke ...
