线性最小二乘法的原则是使得误差的平方和最小，即

为了使S最小，令其对参数的偏导数为零：

即

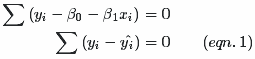
即

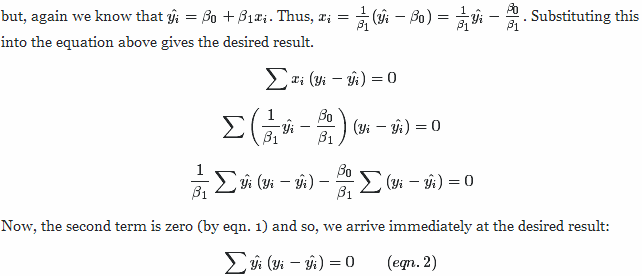
根据方程1和方程2，得

又∵

∴

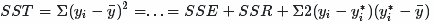
参考链接：https://math.stackexchange.com/questions/709419/prove-sst-ssessr

线性回归决定系数之Why SST=SSE+SSR的更多相关文章

  1. （转）决定系数R2

    有些讲得太烂了,我来通俗的梳理一下R2. Calculating R-squared 在线性回归的模型下,我们可以计算SE(line), SE(y均值). The statistic R2descri ...

  2. SSE,MSE,RMSE,R-square指标讲解

    SSE(和方差.误差平方和):The sum of squares due to errorMSE(均方差.方差):Mean squared errorRMSE(均方根.标准差):Root mean ...

  3. SSE,MSE,RMSE,R-square 指标讲解

    SSE(和方差.误差平方和):The sum of squares due to error MSE(均方差.方差):Mean squared errorRMSE(均方根.标准差):Root mean ...

  4. Data Mining： SSE,MSE,RMSE,R-square指标讲解

    转载自:http://blog.csdn.net/l18930738887/article/details/50629409 SSE(和方差.误差平方和):The sum of squares due ...

  5. 【数学建模】day08-数理统计III

    2. 回归分析 回归分析与曲线拟合区分. 曲线拟合是,根据得到的若干有关变量的一组数据,寻找因变量与(一个或几个)自变量之间的一个函数,使这个函数对那组数据拟合得好.通常,函数的形式可以由经验.先验知 ...

  6. Regression analysis

    Source: http://wenku.baidu.com/link?url=9KrZhWmkIDHrqNHiXCGfkJVQWGFKOzaeiB7SslSdW_JnXCkVHsHsXJyvGbDv ...

  7. matlab 万能实用的非线性曲线拟合方法

    ——转载网络 在科学计算和工程应用中,经常会遇到需要拟合一系列的离散数据,最近找了很多相关的文章方法,在这里进行总结一下其中最完整.几乎能解决所有离散参数非线性拟合的方法 第一步:得到散点数据 根据你 ...

  8. Python数模笔记-Sklearn（4）线性回归

    1.什么是线性回归? 回归分析(Regression analysis)是一种统计分析方法,研究自变量和因变量之间的定量关系.回归分析不仅包括建立数学模型并估计模型参数,检验数学模型的可信度,也包括利 ...

  9. 回归分析|r^2|Se|变差|多重相关系数|决定系数|多重共线性|容忍度|VIF|forward selection|backward elimination|stepwise regression procedure|best-subset approach|回归方程的置信区间|预测区间|残差分析|虚拟变量

    应用统计学-回归分析 拟合度使用r^2和Se来检验. 显著性检验中,对于线性model使用ANOVA,对于单独的回归系数使用t检验. 最小二乘法.贝叶斯和最大似然都可用于求回归参数,最小二乘法是最小化 ...

随机推荐

  1. Python 传递任意数量的实参

    在定义函数的时候如果你不知道该函数在使用的时候要接收多少的实参怎么办? 好在python提供了可以接收任意数量的实参的操作. # def sandwitch(*ingredents): # print ...

  2. pymysql 数据库编程

    1.引入模块 import pymysql 2.用于建立与数据库的连接 调用pymysql模块中的connect()方法 conn = pymysql.connect(host='localhost' ...

  3. x1c 2018 体验

    总结一下: 2018对比2017优点: 1屏幕完爆:HDR WHD镜面屏完爆 FHD 雾面屏(污+雾,所谓的油腻感),还有色彩!正红色第一次觉得这么好看.别人看得出来看不出来我不知道,至少我能看出来非 ...

  4. Codeforces 984 D - XOR-pyramid

    D - XOR-pyramid 思路: 区间dp dp[l][r]表示ƒ([l, r])的值 显然,状态转移方程为dp[l][r] = dp[l][r-1] ^ dp[l+1][r] 初始状态dp[i ...

  5. 如何模拟一个http请求并把response的内容保存下载下来，导出到excel中（结尾福利）

    def doExport(self): # 模拟一个http请求 url = u'%s?dumptype=investigation&dumpid=%s&timezone=8' % ( ...

  6. CRC分段校验

    crc16 modbus分段校验码: const uint8_t ModbusCRCHighTab[] = { 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x ...

  7. (4)进程---daemon守护线程和join阻塞

    join ()方法:主线程A中,创建了子线程B,并且在主线程A中调用了B.join(),那么,主线程A会在调用的地方等待,直到子线程B完成操作后,才可以接着往下执行,那么在调用这个线程时可以使用被调用 ...

  8. LeetCode--242--有效的字母异位词

    问题描述: 给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的一个字母异位词. 示例 1: 输入: s = "anagram", t = "nagara ...

  9. 20180226xlVbaGetStockData

    Sub LoopGetStockData() Dim StartTime As Variant Dim UsedTime As Variant StartTime = VBA.Timer Cells. ...

  10. bzoj3884: 上帝与集合的正确用法 扩展欧拉定理

    题意:求\(2^{2^{2^{2^{...}}}}\%p\) 题解:可以发现用扩展欧拉定理不需要很多次就能使模数变成1,后面的就不用算了 \(a^b\%c=a^{b\%\phi c} gcd(b,c) ...