Bzoj2673 3961: [WF2011]Chips Challenge 费用流

国际惯例题面: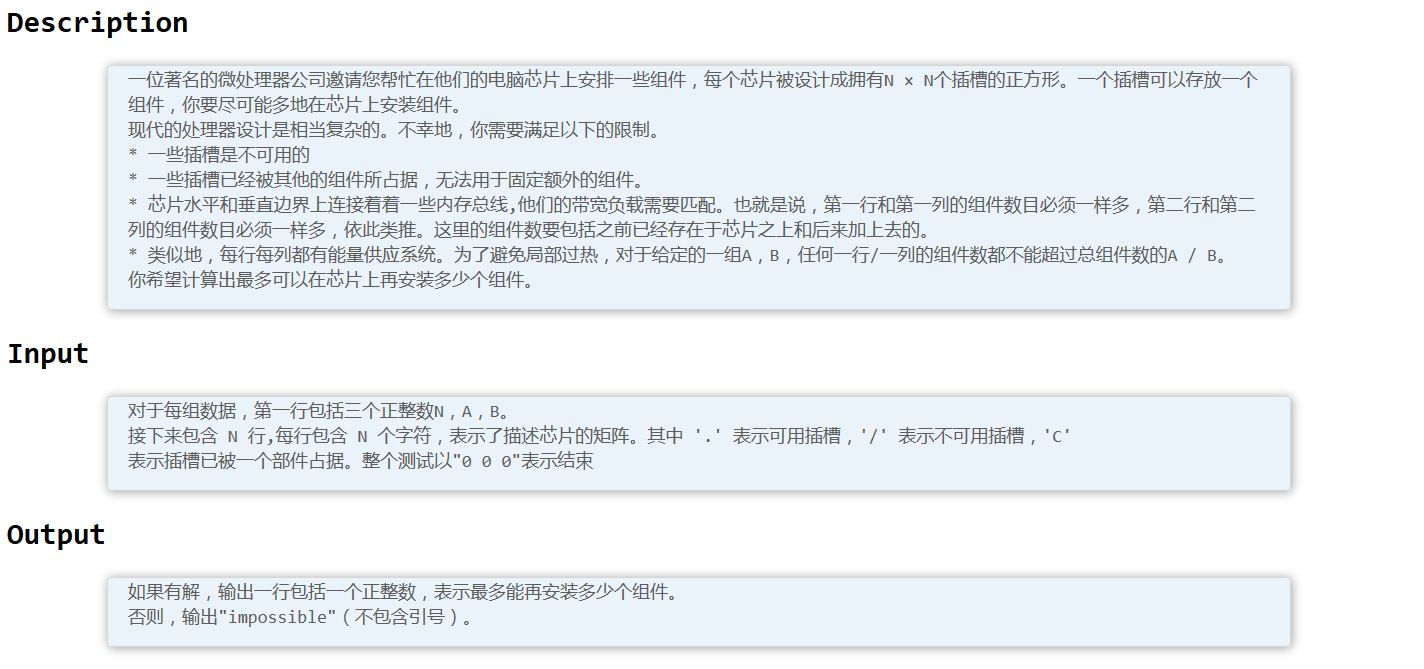

如果我们枚举放几个零件的话，第二个限制很容易解决，但是第一个怎么办？(好的，这么建图不可做)
考虑我们枚举每行每列最多放几个零件t，然后计算零件总数sum。这样如果可行的话，则有t*B<=sum*A。
考虑第一个限制怎么办。我们可以钦定所有可行的位置都放上零件，然后再把多的零件拆下来。
我们令sxi为第i行能放的最多零件数，syi为第i列能放的最多零件数。
由源点向每一行连流量sxi费用0的边，每一列向汇点连流量syi费用0的边。
然后让每一行i向每一列i连流量t费用0的边，表示第i行和第j列最多同时不拆(留下)t个零件。
最后对于所有输入为'.'的格子ij，由第i行向第j列连容量1费用1的边，表示拆下第i行第j列的零件。
跑费用流，必须满流才满足题意(零件要么行和列同时留下，要么拆掉)，费用表示拆掉的零件个数。
然后用留下的零件个数和t去比较是否合法，计算答案就行了。
感觉这题就是给了我们一种网络流建图，补集转化的姿势(如果选择的流量行列不移动统一，那么去掉的流量是否统一？如果选择的不好限制，去掉的是否容易限制？)

代码:

 #pragma GCC optimize(2)
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<queue>
 const int maxn=1e2+1e1,maxe=maxn*maxn;
 const int inf=0x3f3f3f3f;

 char in[maxn][maxn];
 int s[maxn],t[maxe<<],nxt[maxe<<],f[maxe<<],c[maxe<<],cnt;
 int dis[maxn],inq[maxn],ins[maxn],st,ed,cst;
 int sx[maxn],sy[maxn],su,ini;
 int n,A,B,ans;

 inline void coredge(int from,int to,int flow,int cost) {
     t[++cnt] = to , f[cnt] = flow , c[cnt] = cost ,
     nxt[cnt] = s[from] , s[from] = cnt;
 }
 inline void singledge(int from,int to,int flow,int cost) {
     coredge(from,to,flow,cost) , coredge(to,from,,-cost);
 }
 inline bool spfa() {
     memset(dis,0x3f,sizeof(dis)) , dis[st] = ;
     std::queue<int> q; q.push(st) , inq[st] = ;
     while( q.size() ) {
         const int pos = q.front(); q.pop() , inq[pos] = ;
         for(int at=s[pos];at;at=nxt[at])
             if( f[at] && dis[t[at]] > dis[pos] + c[at] ) {
                 dis[t[at]] = dis[pos] + c[at];
                 if( !inq[t[at]] ) q.push(t[at]) , inq[t[at]] = ;
             }
     }
     return dis[ed] != inf;
 }
 inline int dfs(int pos,int flow) {
     if( pos == ed ) return flow;
     int ret =  , now = ; ins[pos] = ;
     for(int at=s[pos];at;at=nxt[at])
         if( f[at] && !ins[t[at]] && dis[t[at]] == dis[pos] + c[at] ) {
             now = dfs(t[at],std::min(flow,f[at])) ,
             ret += now , flow -= now , cst += c[at] * now ,
             f[at] -= now , f[at^] += now;
             if( !flow ) return ins[pos] =  , ret;
         }
     if( !ret ) dis[pos] = inf;
     return ins[pos] =  , ret;
 }
 inline int flow() { // we must got full flow .
     int ret =  , now = ;
     while( spfa() ) while( ( now = dfs(st,inf) ) ) ret += now;
     return ret;
 }

 inline void build(int t) {
     memset(s,,sizeof(s)) , cnt =  , st = n *  +  , ed = st +  , cst = ;
     #define cov(x,id) (x*2-1+id)
     for(int i=;i<=n;i++) {
         singledge(st,cov(i,),sx[i],) ,
         singledge(cov(i,),cov(i,),t,) ,
         singledge(cov(i,),ed,sy[i],) ;
     }
     for(int i=;i<=n;i++) for(int j=;j<=n;j++) if( in[i][j] == '.' ) singledge(cov(i,),cov(j,),,);
 }
 inline int calc(int t) {
     build(t);
     if( flow() != su ) return -; // illegal .
     int used = su - cst;
     return used * A >= t * B ? used - ini : -;
 }

 int main() {
     static int cse;
     while( scanf("%d%d%d",&n,&A,&B) ==  && ( n || A || B ) ) {
         memset(sx,,sizeof(sx)) , memset(sy,,sizeof(sy)) , ini = su =  , ans = -;
         for(int i=;i<=n;i++) {
             scanf("%s",in[i]+);
             for(int j=;j<=n;j++){
                 if( in[i][j] != '/' ) ++sx[i] , ++sy[j] , ++su;
                 ini += in[i][j] == 'C';
             }
         }
         for(int i=;i<=n;i++) ans = std::max( ans , calc(i) );
         printf("Case %d: ",++cse);
         if( !~ans ) puts("impossible");
         else printf("%d\n",ans);
     }
     return ;
 }

(话说我都多路增广+码内O2了才卡到332MS，那几个几十MS过掉的是怎么做到的)

華やかな 煌びやかな運命を
做着拥有绚烂命运的梦
夢見て 泣いた夜は
却因为这样的梦 止不住泪水
银色の流星も泣いている
银色的流星也在哭泣
ナツシスに向けて
向着水仙花海
あっけなく さよならを告げぬよう
不想轻易说出再见
唇が　告げぬように
所以咬紧双唇
呟きに星空も木霊する
唯有轻声细语回响在星空下
ナツシスに向けて
朝着水仙
いつまでも届け
将它传递到永远