manifold 微分流形上可以定义可微函数、切向量、切向量场、各种张量场等对象并建立其上的分析学，并可以赋予更复杂的几何结构以研究它们的性质。

小结：

1、流形（英语：Manifolds）一般可以通过把许多平直的片折弯并粘连而成，是局部具有欧几里得空间性质的空间，是欧几里得空间中的曲线、曲面等概念的推广

2、描述一个流形往往需要不止一个“地图”，因为一般来说流形并不是真正的欧几里得空间。举例来说，地球就没法用一张平面的地图来合适地描绘。

https://baike.baidu.com/item/微分流形/710877

微分流形（differentiable manifold），也称为光滑流形（smooth manifold），是拓扑学和几何学中一类重要的空间，是带有微分结构的拓扑流形。 微分流形是微分几何与微分拓扑的主要研究对象，是三维欧式空间中曲线和曲面概念的推广，可以有更高的维数，而不必有距离和度量的概念。

https://en.wikipedia.org/wiki/Manifold

3-流形

3-manifold

https://en.wikipedia.org/wiki/3-manifold

In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.

https://en.wikipedia.org/wiki/Torus#n-dimensional_torus

The 3-dimensional torus is the product of 3 circles. That is:

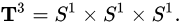
3维环面是3个圆的积

https://zh.wikipedia.org/wiki/流形

流形（英语：Manifolds），是局部具有欧几里得空间性质的空间，是欧几里得空间中的曲线、曲面等概念的推广。欧几里得空间就是最简单的流形的实例。地球表面这样的球面则是一个稍微复杂的例子。一般的流形可以通过把许多平直的片折弯并粘连而成。

流形在数学中用于描述几何形体，它们为研究形体的可微性提供了一个自然的平台。物理上，经典力学的相空间和构造广义相对论的时空模型的四维伪黎曼流形都是流形的实例。位形空间中也可以定义流形。环面就是双摆的位形空间。

一般可以把几何形体的拓扑结构看作是完全“柔软”的，因为所有变形（同胚）会保持拓扑结构不变；而把解析几何结构看作是“硬”的，因为整体的结构都是固定的。例如一个多项式，如果你知道 {\displaystyle (0,1)} 区间的取值，则整个实数范围的值都是固定的，所以局部的变动会导致全局的变化。光滑流形可以看作是介于两者之间的模型：其无穷小的结构是“硬”的，而整体结构则是“柔软”的。这也许是中文译名“流形”的原因（整体的形态可以流动）。该译名由著名数学家和数学教育学家江泽涵引入。这样，流形的硬度使它能够容纳微分结构，而它的软度使得它可以作为很多需要独立的局部扰动的数学和物理的模型。

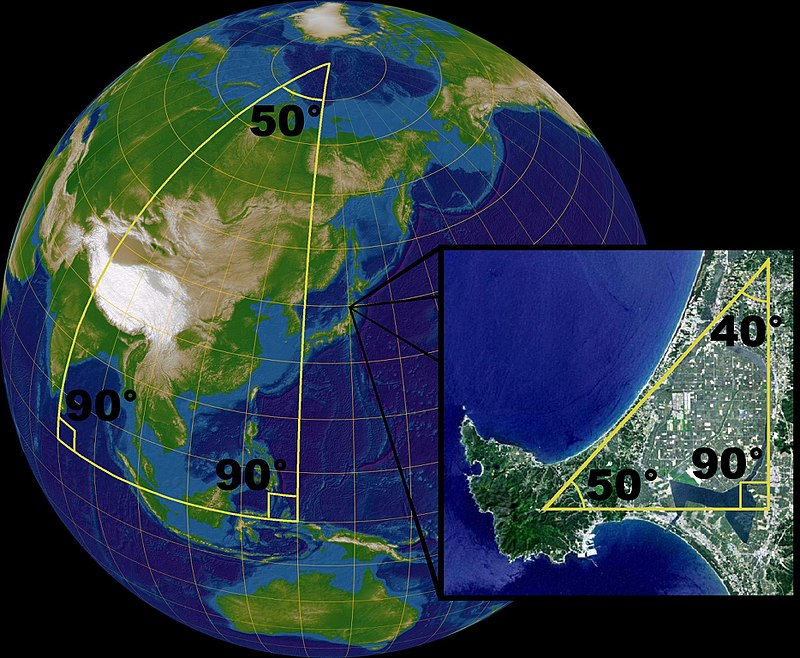
流形可以视为近看起来象欧几里得空间或其他相对简单的空间的物体^[1]:1。例如，人们曾经以为地球是平的。这是因为相对于地球来说人类实在太小，平常看到的地面是地球表面微小的一部分。所以，尽管知道地球实际上差不多是一个圆球，如果只需要考虑其中微小的一部分上发生的事情，比如测量操场跑道的长度或进行房地产交易时，仍然把地面看成一个平面。一个理想的数学上的球面在足够小的区域上的特性就像一个平面，这表明它是一个流形^[2]:283。但是球面和平面的整体结构是完全不同的：如果在球面上沿一个固定方向走，最终会回到起点，而在一个平面上，可以一直走下去。

回到地球的例子。像旅行的时候，会用平面的地图来指示方位。如果将整个地球的各个地区的地图合订成一本地图集，那么在观看各个地区的地图后，就可以在脑海中“拼接”出整个地球的景貌。为了能让阅读者顺利从一张地图接到下一张，相邻的地图之间会有重叠的部分，以便在脑海里“粘合”两张图。类似地，在数学中，也可以用一系列“地图”（称为坐标图或坐标卡）组成的“地图集”（atlas, 亦称为图册）来描述一个流形^[2]:283。而“地图”之间重叠的部分在不同的地图里如何变换，则描述了不同“地图”的相互关系。

描述一个流形往往需要不止一个“地图”，因为一般来说流形并不是真正的欧几里得空间。举例来说，地球就没法用一张平面的地图来合适地描绘。

流形要求局部“看起来像”简单的空间，这不是一个简单的要求。例如，在球上吊一根线，这个整体就不是一个流形。包含了线和球连接的那一点的附近区域一定不是简单的：既不是线也不是面，无论这个区域有多小。

流形有很多种。最简单的是拓扑流形，它们局部看来像欧几里得空间。其他的种类包含了它们在使用中所需要的额外的结构。例如，一个微分流形不仅支持拓扑，而且要支持微积分。黎曼流形的思想导致了广义相对论的数学基础，使得人们能够用曲率来描述时空。

https://zh.wikipedia.org/wiki/拓扑学

拓扑学可定义为“对特定对象（称为拓扑空间）在特定变换（称为连续映射）下不变之性质的研究，尤其是那些在特定可逆变换（称为同胚）下不变之性质。”

拓扑学可定义为“对特定对象（称为拓扑空间）在特定变换（称为连续映射）下不变之性质的研究，尤其是那些在特定可逆变换（称为同胚）下不变之性质。”

拓扑被用来指附加于一集合 X 上的结构，该结构基本上会将集合 X 描绘成一拓扑空间，使之能处理在变换下的收敛性、连通性与连续性等性质。

拓扑空间几乎会自然地出现在数学的每个分支里。这使得拓扑学成为数学中的重要统合概念之一。

激励拓扑学里的洞见来自于一些不依靠对象实际形状，而是其组织方式的几何问题。例如，正方形与圆形有许多共通之性质：两者（自拓扑学的观点来看）均为一维对象，且都能将平面分成外部及内部两个部分。

在拓扑学的第一篇论文中，李昂哈德·欧拉证明，不可能找到一条通过柯尼斯堡（现为加里宁格勒）的路，且七座桥都恰只通过一次。此一结论不依靠桥的长度，以及其之间的距离，而只与其连通性质有关：哪座桥会连接哪两座岛与河岸。这个问题被称为柯尼斯堡七桥问题，且导致了图论的发展。

 

在拓扑学中，一个杯子和一个面包圈（实心环面）是相同的

同样地，代数拓扑上的毛球定理表示，“没有人能抚平毛球上的毛，而没有翘起的毛。”这个事实能立即让大多数人信服，尽管他们可能不知道该定理更形式化的陈述，即球体上不存在非零连续切向量场。如同“柯尼斯堡七桥问题”一般，此一结论亦不依靠球体的形状，而可适用于任何一类光滑表面，只要表面上没有洞。

为了处理这些不依靠对象实际形状的问题，必须清楚知道这些问题只依靠着何种性质。这产生出了同胚的概念。不可能只穿越每座桥一次能适用于其排列同胚于那些在柯尼斯堡里七座桥之桥梁；而毛球定理也适用于任何与球体同胚之形状。

直观上来看，两个空间同胚，若其中一个空间可不须切开或黏合即可变形成另一个空间。一个古老的笑话为，拓扑学无法分辨咖啡杯与甜甜圈，因为足够柔软的甜甜圈可被凹成一个杯底，中间的洞则可缩成一个手柄。

同胚可以被认为是最基本的“拓扑等价”。另一种为同伦等价。很难不使用到专业术语来描述同伦，但其中一个重要的概念为，两个对象为同伦等价，若两者都可由某个较大的对象“压扁”而成。