图->存储结构->十字链表

文字描述

　　十字链表是有向图的另一种链式存储结构. 在十字链表中,对应于有向图中每一条弧有一个结点,对应于每个顶点也有一个结点.这些结点的结构如下所示:

　　在弧结点中有5个域: 尾域tailvex和头域headvex分别指示弧尾和弧头这两个顶点在图中的位置,链域hlink指向与弧头相同的下一条弧, 而链域tlink指向弧尾相同的下一条弧, info域指向该弧的相关信息; 弧头相同的弧在同一链表上, 弧尾相同的弧也在同一链表上. 它们的头结点即为顶点结点,它由3个域组成:其中data域存储和顶点相关的信息,如顶点名称等; firstin和firstout为两个链域,分别指向以该顶点为弧头或弧尾的第一个弧结点.

示意图

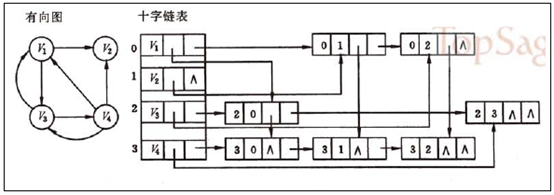
算法分析

　　建立十字链表的时间复杂度和建立邻接表是相同的. 而且在十字链表中既容易找到以vi为尾的弧,也容易找到以vi为头的弧,因而容易求得顶点的出度和入度.

代码实现

 /*
     以十字链表作为图的存储结构创建图。
 */
 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>

 #define    MAX_VERTEX_NUM    20    //最大顶点数
 #define DEBUG
 typedef enum {DG, DN, UDG, UDN} GraphKind; //{有向图，有向网，无向图，无向网}
 typedef char InfoType;
 typedef char VertexType;
 //弧结点
 typedef struct ArcBox{
     int tailvex, headvex;//该弧的尾和头顶点的位置
     struct ArcBox *hlink, *tlink;//分别为弧头相同和弧尾相同的弧的链域
     InfoType *info;//该弧相关的信息
 }ArcBox;
 //顶点结点
 typedef struct VexNode{
     VertexType data;//顶点名称
     ArcBox *firstin, *firstout;//分别指向该顶点第一条入弧和出弧
 }VexNode;
 typedef struct{
     VexNode xlist[MAX_VERTEX_NUM];//表头向量
     int vexnum, arcnum;//有向图的当前顶点数和弧数
     GraphKind kind;//图类型
 }OLGraph;

 /*
     若G中存在顶点u，则返回该顶点在图中位置；否则返回-1。
 */
 int LocateVex(OLGraph G, VertexType v)
 {
     int i = ;
     for(i=; i<G.vexnum; i++){
         if(G.xlist[i].data == v)
             return i;
     }
     return -;
 }

 /*
     若G中存在顶点位置loc存在,则返回其顶点名称
 */
 VertexType LocateVInfo(OLGraph G, int loc)
 {
     return G.xlist[loc].data;
 }

 /*
     采用十字链表的存储结构，构造有向图
  */
 int CreateDG(OLGraph *G)
 {
     int i = , j = , k = , IncInfo = ;
     int v1 = , v2 = ;
     char tmp[] = {};
     ArcBox *p = NULL;

     printf("输入顶点数，弧数，其他信息标志位: ");
     scanf("%d,%d,%d", &G->vexnum, &G->arcnum, &IncInfo);

     for(i=; i<G->vexnum; i++){
         //输入顶点值
         printf("输入第%d个顶点: ", i+);
         memset(tmp, , sizeof(tmp));
         scanf("%s", tmp);
         //初始化指针
         G->xlist[i].data = tmp[];
         G->xlist[i].firstin = NULL;
         G->xlist[i].firstout = NULL;
     }

     //输入各弧并构造十字链表
     for(k=; k<G->arcnum; k++){
         printf("输入第%d条弧(顶点1, 顶点2): ", k+);
         memset(tmp, , sizeof(tmp));
         scanf("%s", tmp);
         sscanf(tmp, "%c,%c", &v1, &v2);
         //确定顶点v1和v2在图中的位置
         i = LocateVex(*G, v1);
         j = LocateVex(*G, v2);
         //对弧结点赋值
         p = (ArcBox *) malloc(sizeof(ArcBox));
         p->tailvex = i;
         p->headvex = j;
         p->hlink = G->xlist[j].firstin;
         p->tlink = G->xlist[i].firstout;
         p->info = NULL;
         //完成在入弧和出弧链头的插入
         G->xlist[j].firstin = p;
         G->xlist[i].firstout = p;
         //若弧有相关的信息,则输入
         if(IncInfo){
             //Input(p->info);
         }
     }
     return ;
 }

 /*
     采用十字链表的存储结构，构造图
 */
 int CreateGraph(OLGraph *G)
 {
     printf("输入图类型: +有向图(0), -有向网(1), -无向图(2), -无向网(3): ");
     scanf("%d", &G->kind);
     switch(G->kind){
         case DG:
             return CreateDG(G);
         case DN:
         case UDN:
         case UDG:
         default:
             printf("还不支持!\n");
             return -;
     }
 }

 /*
     输出图的信息
 */
 void printG(OLGraph G)
 {
     if(G.kind == DG){
         printf("类型：有向图；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }else if(G.kind == DN){
         printf("类型：有向网；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }else if(G.kind == UDG){
         printf("类型：无向图；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }else if(G.kind == UDN){
         printf("类型：无向网；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }

     int i = ;
     ArcBox *fi = NULL;
     ArcBox *fo = NULL;
     for(i=; i<G.vexnum; i++){
         printf("%c: ", G.xlist[i].data);
         fi = G.xlist[i].firstin;
         fo = G.xlist[i].firstout;
         printf("(hlink=");
         while(fi){
 #ifdef DEBUG
             printf("%c->%c; ", LocateVInfo(G, fi->tailvex), LocateVInfo(G, fi->headvex));
 #else
             printf("%d->%d; ", fi->tailvex, fi->headvex);
 #endif
             fi = fi->hlink;
         }
         printf(")\t(tlink=");
         while(fo){
 #ifdef DEBUG
             printf("%c->%c; ", LocateVInfo(G, fo->tailvex), LocateVInfo(G, fo->headvex));
 #else
             printf("%d->%d; ", fo->tailvex, fo->headvex);
 #endif
             fo = fo->tlink;
         }
         printf(")\n");
     }
     return;
 }

 int main(int argc, char *argv[])
 {
     OLGraph G;
     if(CreateGraph(&G) > -){
         printG(G);
     }
     return ;
 }

十字链表存储结构(图)

代码运行