L1与L2正则化

目录

• 过拟合
• 结构风险最小化原理
• 正则化
• L2正则化
• L1正则化
• L1与L2正则化
• 参考链接

过拟合

机器学习中，如果参数过多、模型过于复杂，容易造成过拟合。

结构风险最小化原理

在经验风险最小化（训练误差最小化）的基础上，尽可能采用简单的模型，以提高模型泛化预测精度。

正则化

为了避免过拟合，最常用的一种方法是使用正则化，例如L1和L2正则化。

所谓的正则化，就是在原来损失函数的基础上，加了一些正则化项，或者叫做模型复杂度惩罚项。

L2正则化

L2正则化即：\(L=E_{in}+\lambda\sum_j\omega^2_j\)，其中，\(E_{in}\)是原来的损失函数；\(\lambda\)是正则化参数，可调整；\(\omega_j\)是参数。

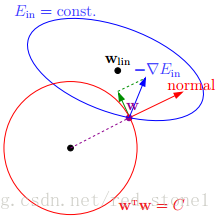
由上可知，正则化是为了限制参数过多，避免模型过于复杂。因此，我们可以令高阶部分的权重\(\omega\)为0，这样就相当于从高阶转换为低阶。然而，这是个NP难问题，将其适度简化为：\(\sum_j\omega_j^2≤C\)，令\(\omega_j\)的平方和小于\(C\)。这时，我们的目标就转换为：令\(E_{in}\)最小，但是要遵循\(w\)平方和小于\(C\)的条件，如下图所示：

L1正则化

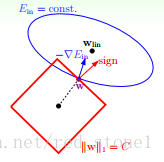
L1正则化和L2正则化相似：\(L=E_{in}+\lambda\sum_j|\omega_j|\)，同样地，图形如下：

L1与L2正则化

满足正则化条件，实际上是求解上面图中红色形状与蓝色椭圆的交点，即同时满足限定条件和\(E_{in}\)最小化。

对于L2来说，限定区域是圆，这样得到的解\(\omega_1\)或\(\omega_2\)（以二元为例）为0的概率很小，且很大概率是非零的。

对于L1来说，限定区域是正方形，方形与蓝色区域相交的交点是顶点的概率很大，这从视觉和常识上来看是很容易理解的。也就是说，正方形的凸点会更接近 \(E_{in}\)最优解对应的\(\omega\)位置，而凸点处必有\(\omega_1\)或\(\omega_2\)为0。这样，得到的解\(\omega_1\)或\(\omega_2\)为零的概率就很大了。所以，L1正则化的解具有稀疏性。

扩展到高维，同样的道理，L2的限定区域是平滑的，与中心点等距；而 L1 的限定区域是包含凸点的，尖锐的。这些凸点更接近\(E_{in}\)的最优解位置，而在这些凸点上，很多\(\omega_j\)为0。

参考链接

https://www.jianshu.com/p/76368eba9c90

https://segmentfault.com/a/1190000014680167?utm_source=tag-newest

https://blog.csdn.net/red_stone1/article/details/80755144

---

作者：@臭咸鱼

转载请注明出处：https://www.cnblogs.com/chouxianyu/

欢迎讨论和交流!

---