【杂题】cf1041fF. Ray in the tube

死于没有处理边界

题目描述

题目大意

在两面镜子上各选定一个整数位置的点 A 与 B，并从其中一个点向另一个射出一条光线，使得接收到光线的传感器数量尽可能的多。传感器不重叠。

---

题目分析

我们来初步考虑一下答案路径的形式。

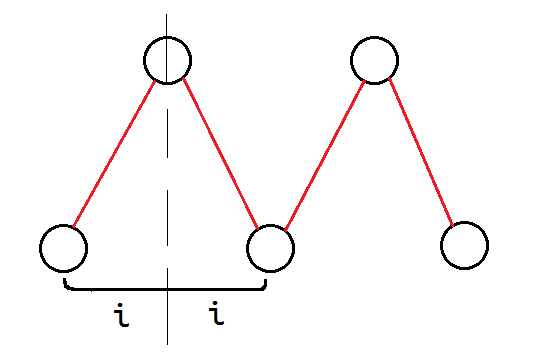
1.$i$为奇数：那么我们以步长$1$去走，不仅一定经过最优答案的路径，还有可能会走过其他传感器。因此步长$1$囊括了所有$i$为奇数的情况。

2.$i$为偶数：沿用上续思路，用步长$2$去试试？发现$path=4k+2$.也就是说还剩下所有距离$4k$的点走不到.如果接着用步长$8$呢？那么$path=8k+4$.

这意味着我们枚举$\log_22\times10^9$次步长，每次$n\log_2n$验证，就覆盖了所有走法。

死于没有处理$ans=2$的初值。

 #pragma GCC optimize(2)
 #include<bits/stdc++.h>
 typedef long long ll;
 const int maxn = ;
 const int Det = ;

 int n,m,h,ans;
 int a[maxn],b[maxn],s[maxn],t[maxn],sap[maxn];

 int read()
 {
     char ch = getchar();
     int num = , fl = ;
     for (; !isdigit(ch); ch=getchar())
         if (ch=='-') fl = -;
     for (; isdigit(ch); ch=getchar())
         num = (num<<)+(num<<)+ch-;
     return num*fl;
 }
 void Gap(ll x)
 {
 //    printf("x:%lld\n",x);
     for (int i=; i<=n; i++) s[i] = a[i]%x;
     for (int i=; i<=m; i++) t[i] = (1ll*b[i]+x/)%x;
     std::sort(s+, s+n+);
     std::sort(t+, t+m+);
     for (int L=,R=; L<=n; ++L)
     {
         int cnta = , cntb = ;
         for (; s[L+]==s[L]&&L<n; ++L) ++cnta;
         for (; t[R] < s[L]&&R < m; ++R);
         for (; (t[R]==s[L])&&R<=m; ++R) ++cntb;
         ans = std::max(ans, cnta+cntb);
     }
     for (int i=; i<=m; i++) sap[i] = t[i];
     for (int i=; i<=n; i++) t[i] = s[i];
     for (int i=; i<=m; i++) s[i] = sap[i];
     std::swap(n, m);
     for (int L=,R=; L<=n; ++L)
     {
         int cnta = , cntb = ;
         for (; s[L+]==s[L]&&L<n; ++L) ++cnta;
         for (; t[R] < s[L]&&R < m; ++R);
         for (; (t[R]==s[L])&&R<=m; ++R) ++cntb;
         ans = std::max(ans, cnta+cntb);
     }
     std::swap(n, m);
 }
 int main()
 {
     freopen("mirror.in","r",stdin);
     freopen("mirror.out","w",stdout);
     n = read(), m = read(), h = read(), ans = ;
     for (int i=; i<=n; i++) a[i] = read()+Det;
     for (int i=; i<=m; i++) b[i] = read()+Det;
     for (ll i=; i<=2ll*Det; i*=2ll) Gap(i);
     printf("%d\n",ans);
     return ;
 }

cf上还有一种比我 快4倍 的分治做法，除了没怎么看懂都挺好的。

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 #define Rep(i,a,b) for(register int i=(a);i<=int(b);++i)
 #define Dep(i,a,b) for(register int i=(a);i>=int(b);--i)
 #define rep(i,a,b) for(register int i=(a);i<int(b);++i)
 #define mem(x,v) memset(x,v,sizeof(x))
 inline char gc(){
     static char buf[],*p1=buf,*p2=buf;
     return p1==p2&&(p2=(p1=buf)+fread(buf,,,stdin),p1==p2)?EOF:*p1++;
 }
 #define pc putchar
 #define fi first
 #define se second
 #define debug(x) cout << #x" = " << x << endl;
 #define pp(x,y) cout << "pp: " << x << " " << y << endl;
 #define rank __RANK
 inline ll read(){
     register ll x=,f=;register char c=gc();
     for(;!isdigit(c);c=gc())if(c=='-')f=-;
     for(;isdigit(c);c=gc())x=(x<<)+(x<<)+(c^);
     return x*f;
 }
 #define rd read
 void write(ll x){if(x<)x=-x,pc('-');if(x>=)write(x/);putchar(x%+'');}
 void writeln(ll x){write(x);puts("");}
 const int maxn = 1e5+;
 int a[][maxn],tmp[][maxn];
 int n,m;
 int ans = ;
 int cnt[][];
 #define max(a,b) ((a) < (b) ? (b) : (a))
 inline void solve(int l0,int r0,int l1,int r1){
     if((l0>r0) || (l1>r1)){
         if(l0<=r0) ans = max(ans,r0-l0+);
         if(l1<=r1) ans = max(ans,r1-l1+);
         return ;
     }
     if(a[][r0]==&&a[][r1]==) return ;
     Rep(i,l0,r0) tmp[][i] = a[][i];
     Rep(i,l1,r1) tmp[][i] = a[][i];
     cnt[][]=cnt[][]=cnt[][]=cnt[][]=;
     Rep(i,l0,r0)
         if(i==l0 || a[][i] != a[][i-])
             cnt[][a[][i]&]++;

     Rep(i,l1,r1)if(i==l1 || a[][i] != a[][i-])cnt[][a[][i]&]++;
     ans = max(max(ans,cnt[][]+cnt[][]),cnt[][]+cnt[][]);
     int L0 = l0,R0 = r0;
     Rep(i,l0,r0)if(tmp[][i]&)a[][L0++] = tmp[][i]>>;
     Dep(i,r0,l0)if(!(tmp[][i]&))a[][R0--] = tmp[][i]>>;
     int L1 = l1,R1 = r1;
     Rep(i,l1,r1)if(tmp[][i]&) a[][L1++] = tmp[][i]>>;
     Dep(i,r1,l1)if(!(tmp[][i]&))a[][R1--] = tmp[][i]>>;
     solve(l0,L0-,l1,L1-);
     solve(R0+,r0,R1+,r1);
 }
 int main(){
     n = rd();rd();
     ans = ;
     Rep(i,,n) a[][i]=rd();
     sort(a[]+,a[]++n);
     m = rd();rd();
     Rep(i,,m) a[][i]=rd();
     sort(a[]+,a[]++m);
     if(n==&&m==&&a[][]==a[][]){
         puts("");
         return ;
     }
     solve(,n,,m);
     writeln(ans);
     return ;
 }

END