SciTech-BigDataAIML-Algorithm-Heuristic启发式- 带weight(权重)的Graph(无向图)最优路线规划 : Dijkstra Algorithm(迪杰斯特拉算法)"由"边线加权"的Graph"得出"Routing Table(最优路由表)"

Dijkstra迪杰斯特拉算法

用“Graph”作出简图：

图例：

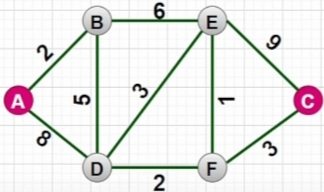
"选定起点"的Routing Table(路由表)

行号	节点	最短距离	前一节点	已访问完全
1	A	0	A	T
2	B	2	A	T
3	C	12	F	T
4	D	7	B	T
5	E	8	B	T
6	F	9	D,E	T

上表的用法:

• 表格的"第1行"是"起点"; 图例：上表是图上的节点"A"作为起点;
• 由"终点"起始,用"每一节点"查表得到的"前一节点";
  
  一步步倒推，可得出 "起点" 到 "终点" 的 "最短完整路线".
  
  例如：要求解“A点出发，到C点的最短路线”，
  
  根据上表，可查表得出：
  • 终点"C"节点的数据记录行的"行号"是 "3"(第3行)，
  • "最短路线" 为12(由"起点A"到"终点C"),
  • "最短完整路线"("起点A"到"终点C"):
    
    由终点C起始, 递推的用"每一节点"查表得到的"前一节点", 一步步倒推, 可得出:
    
    $ C \overset{3}{\leftarrow} F \overset{2}{\leftarrow} D \overset{5}{\leftarrow} B \overset{2}{\leftarrow} A $
  • 注意："最短路径"可能有不只一条；
    
    例如: "起点A"到"终点F"的"最短路线"(最短距离都为9)
    • $ F \overset{2}{\leftarrow} D \overset{5}{\leftarrow} B \overset{2}{\leftarrow} A $
    • $ F \overset{1}{\leftarrow} E \overset{6}{\leftarrow} B \overset{2}{\leftarrow} A $

由"节点路线Graph"推导出"Routing Table(路由表)"

将 Graph 转化为 Dictionary 数据结构:

例如图示的 Graph 可转化为:

MAX_DIST = 99999999
DIST_INDEX = 0
PREV_INDEX = 1
SOURCE = "A"

graph_dict = { # Graph 转化为 Dictionary 数据结构
 "A": [0, ["A"], ("B", 2), ("D", 8)],
 "B": [MAX_DIST, [], ("A", 2), ("D", 5), ("E", 6)],
 "C": [MAX_DIST, [], ("E", 9), ("F", 3)],
 "D": [MAX_DIST, [], ("A", 8), ("B", 5), ("E", 3), ("F", 2)],
 "E": [MAX_DIST, [], ("B", 6), ("D", 3), ("F", 1), ("C", 9)],
 "F": [MAX_DIST, [], ("D", 2), ("E", 1), ("C", 3)],
}

queue_dict = {}
queue_dict[SOURCE] = graph_dict[SOURCE] # 开始只需要将初始"起点A"加入"任务队列"

while len(queue_dict) > 0: # 需要更新计算“后继”节点的"任务队列"
    (node, val) = result_dict.popitem() # 取出一个任务"节点"
    (min_dist, prev, *edges) = val # 得到其"当前累加权重"，"前一个节点" 和 "其edges"
    print("\n Processing : %r: min_dist:%d, prev:%r" % (node, min_dist, prev))

    for next, weight in edges: # 迭代每一条 edge
        next_val = graph_dict[next]
        accu_dist = min_dist + weight # 由"当前节点" 计算 "下一节点" 的"累加权重"
        if accu_dist < next_val[DIST_INDEX]: # 计算得出"更优"的"累加权重":
            next_val[DIST_INDEX] = accu_dist # 将"更优"的"累加权重"更新到"下一节点"
            next_val[PREV_INDEX] = [node] # "更优"选择的"前一节点", 更新到"下一节点"
            queue_dict[next] = next_val # 有更新的"下一节点"要加入"任务队列"
            print(
                "  Edge from:%r, to:%r, accu_dist:%d, prev:%r"
                % (node, next, accu_dist, next_val[PREV_INDEX])
            )
        elif accu_dist == next_val[DIST_INDEX]: # 多个"前节点"有"同优"的"累加权重"
            if node not in next_val[PREV_INDEX]:
                next_val[PREV_INDEX].append(node) # 追加到"前节点"列表
            print(
                "  Edge from:%r, to:%r, accu_dist:%d, prev:%r"
                % (node, next, accu_dist, next_val[PREV_INDEX])
            )
        else:
            print("  Edge from:%r, to:%r, accu_dist:%d, " % (node, next, accu_dist))

print("\n" + "#" * 10 + "\nRouting Table:\n") # 打印路由表
items = list(graph_dict.items())
for n, val in sorted(items, key=lambda x: x[0]):
    print(
        "Node:%r, accu_dist:% 2d, prev:%r" % (n, val[DIST_INDEX], val[PREV_INDEX])
    )

运行结果：

root@localhost:~/storage/shared/AAAAA# python dijkstra.py

 Processing : 'A': min_dist:0, prev:['A']
  Edge from:'A', to:'B', accu_dist:2, prev:['A']
  Edge from:'A', to:'D', accu_dist:8, prev:['A']

 Processing : 'D': min_dist:8, prev:['A']
  Edge from:'D', to:'A', accu_dist:16,
  Edge from:'D', to:'B', accu_dist:13,
  Edge from:'D', to:'E', accu_dist:11, prev:['D']
  Edge from:'D', to:'F', accu_dist:10, prev:['D']

 Processing : 'F': min_dist:10, prev:['D']
  Edge from:'F', to:'D', accu_dist:12,
  Edge from:'F', to:'E', accu_dist:11, prev:['D', 'F']
  Edge from:'F', to:'C', accu_dist:13, prev:['F']

 Processing : 'C': min_dist:13, prev:['F']
  Edge from:'C', to:'E', accu_dist:22,
  Edge from:'C', to:'F', accu_dist:16,

 Processing : 'E': min_dist:11, prev:['D', 'F']
  Edge from:'E', to:'B', accu_dist:17,
  Edge from:'E', to:'D', accu_dist:14,
  Edge from:'E', to:'F', accu_dist:12,
  Edge from:'E', to:'C', accu_dist:20,

 Processing : 'B': min_dist:2, prev:['A']
  Edge from:'B', to:'A', accu_dist:4,
  Edge from:'B', to:'D', accu_dist:7, prev:['B']
  Edge from:'B', to:'E', accu_dist:8, prev:['B']

 Processing : 'E': min_dist:8, prev:['B']
  Edge from:'E', to:'B', accu_dist:14,
  Edge from:'E', to:'D', accu_dist:11,
  Edge from:'E', to:'F', accu_dist:9, prev:['E']
  Edge from:'E', to:'C', accu_dist:17,

 Processing : 'F': min_dist:9, prev:['E']
  Edge from:'F', to:'D', accu_dist:11,
  Edge from:'F', to:'E', accu_dist:10,
  Edge from:'F', to:'C', accu_dist:12, prev:['F']

 Processing : 'C': min_dist:12, prev:['F']
  Edge from:'C', to:'E', accu_dist:21,
  Edge from:'C', to:'F', accu_dist:15,

 Processing : 'D': min_dist:7, prev:['B']
  Edge from:'D', to:'A', accu_dist:15,
  Edge from:'D', to:'B', accu_dist:12,
  Edge from:'D', to:'E', accu_dist:10,
  Edge from:'D', to:'F', accu_dist:9, prev:['E', 'D']

##########
Routing Table:
Node:'A', accu_dist: 0, prev:['A']
Node:'B', accu_dist: 2, prev:['A']
Node:'C', accu_dist: 12, prev:['F']
Node:'D', accu_dist: 7, prev:['B']
Node:'E', accu_dist: 8, prev:['B']
Node:'F', accu_dist: 9, prev:['E', 'D']